吉林大学学报(工学版) ›› 2019, Vol. 49 ›› Issue (3): 865-871.doi: 10.13229/j.cnki.jdxbgxb20180309

• • 上一篇    下一篇

具有负压缩性的铰接八面体结构的有限元分析

周晓勤1(),杨璐1,张磊1,陈立军2()   

  1. 1. 吉林大学 机械与航空航天工程学院，长春 130022
    2. 吉林大学 大数据和网络管理中心, 长春 130022
  • 收稿日期:2018-04-09 出版日期:2019-05-01 发布日期:2019-07-12
  • 通讯作者: 陈立军 E-mail:xqzhou@jlu.edu.cn;clj@jlu.edu.cn
  • 作者简介:周晓勤（1967?），男，教授，博士生导师. 研究方向：超构材料. E?mail:xqzhou@jlu.edu.cn
  • 基金资助:
    国家自然科学基金项目(51475208)

Finite element analysis of hinging octahedron structure withnegative compressibility

Xiao⁃qin ZHOU1(),Lu YANG1,Lei ZHANG1,Li⁃jun CHEN2()   

  1. 1. College of Mechanical Science and Aerospace Engineering, Jinlin University, Changchun 130022, China
    2. Big Data and Network Management Center, Jilin University, Changchun 130022, China
  • Received:2018-04-09 Online:2019-05-01 Published:2019-07-12
  • Contact: Li?jun CHEN E-mail:xqzhou@jlu.edu.cn;clj@jlu.edu.cn

RICH HTML

 5   

PDF (PC)

404

摘要：

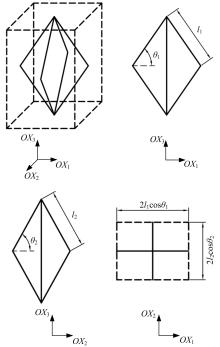
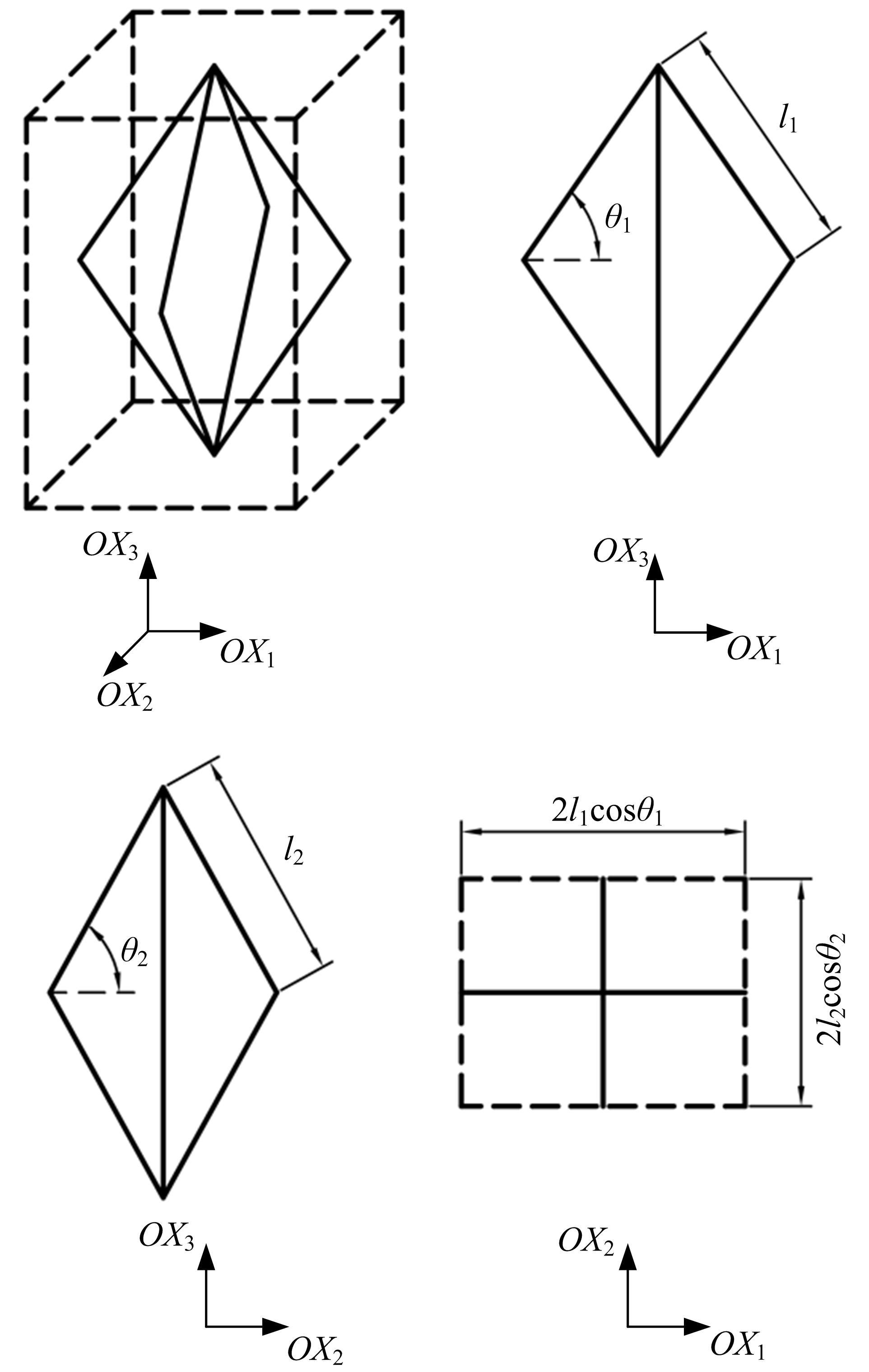
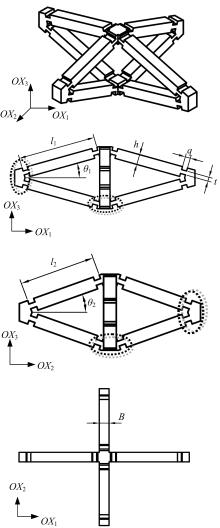
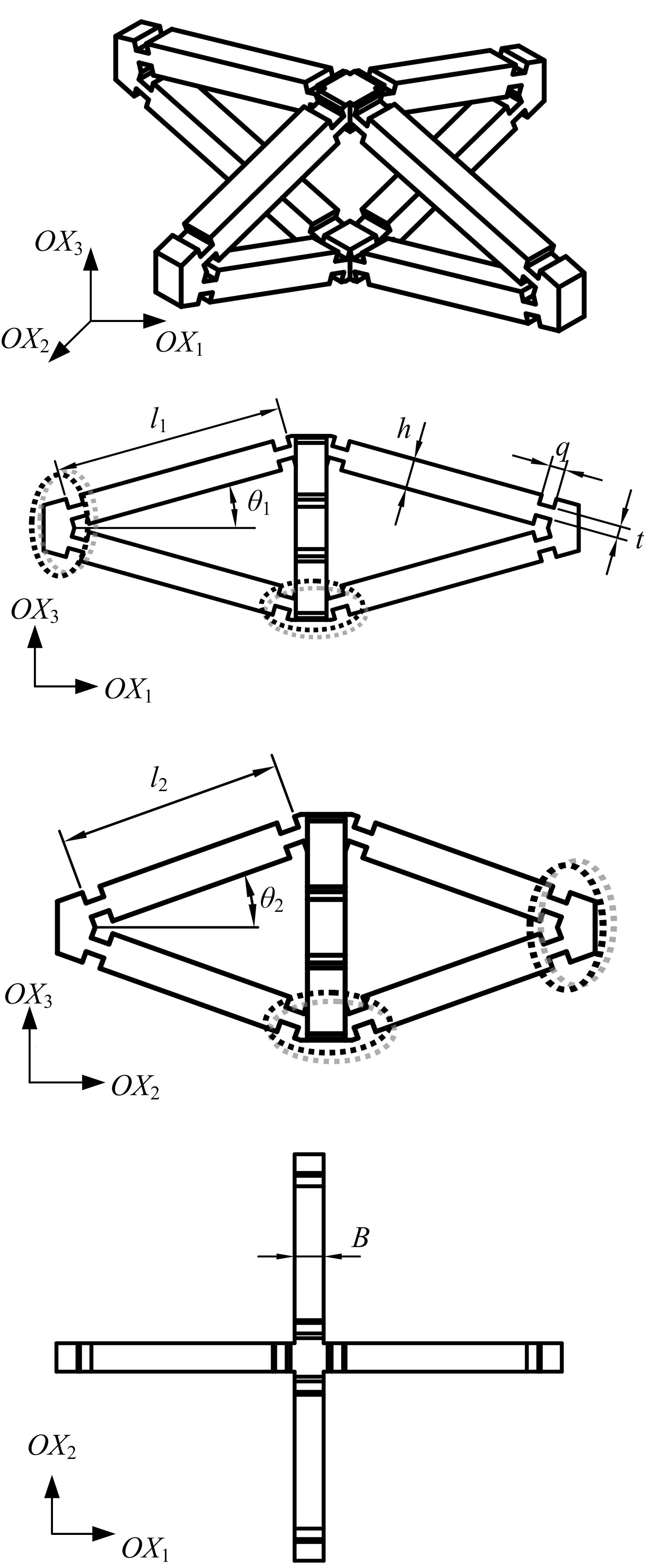
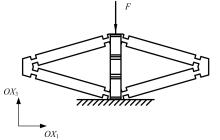
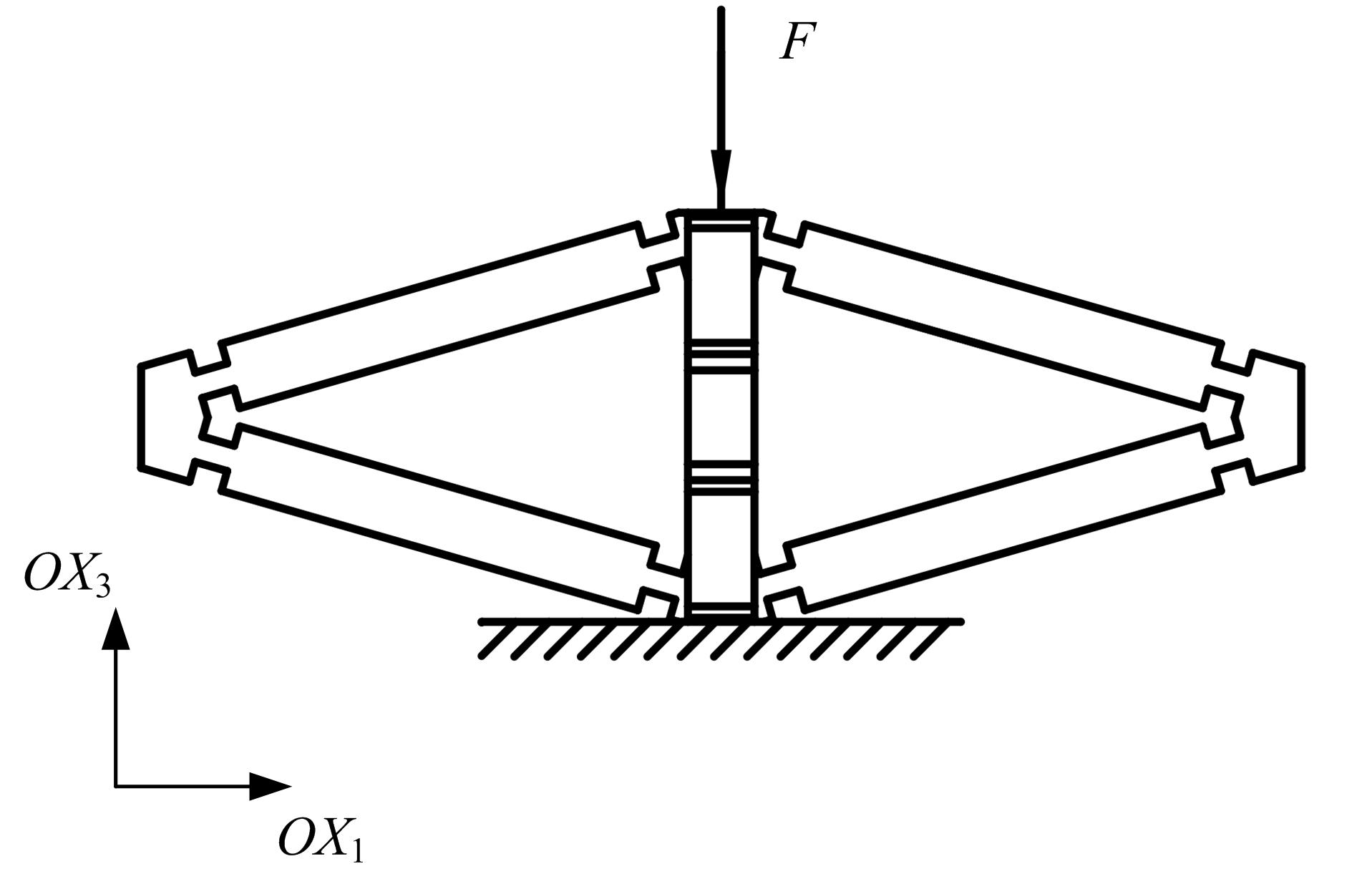
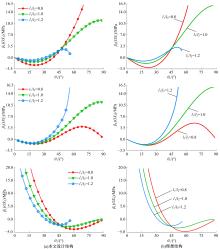
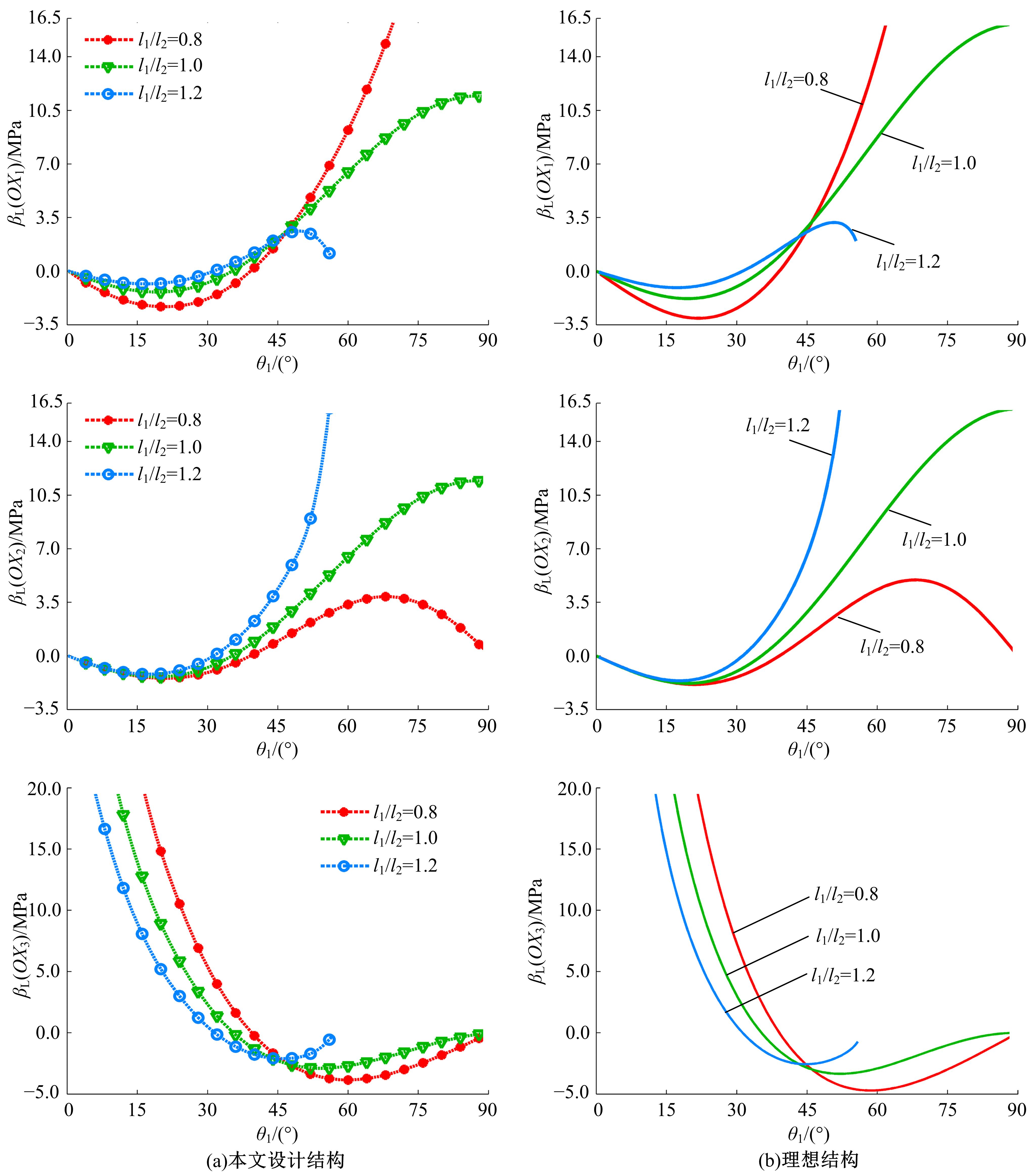
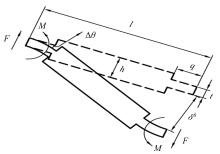
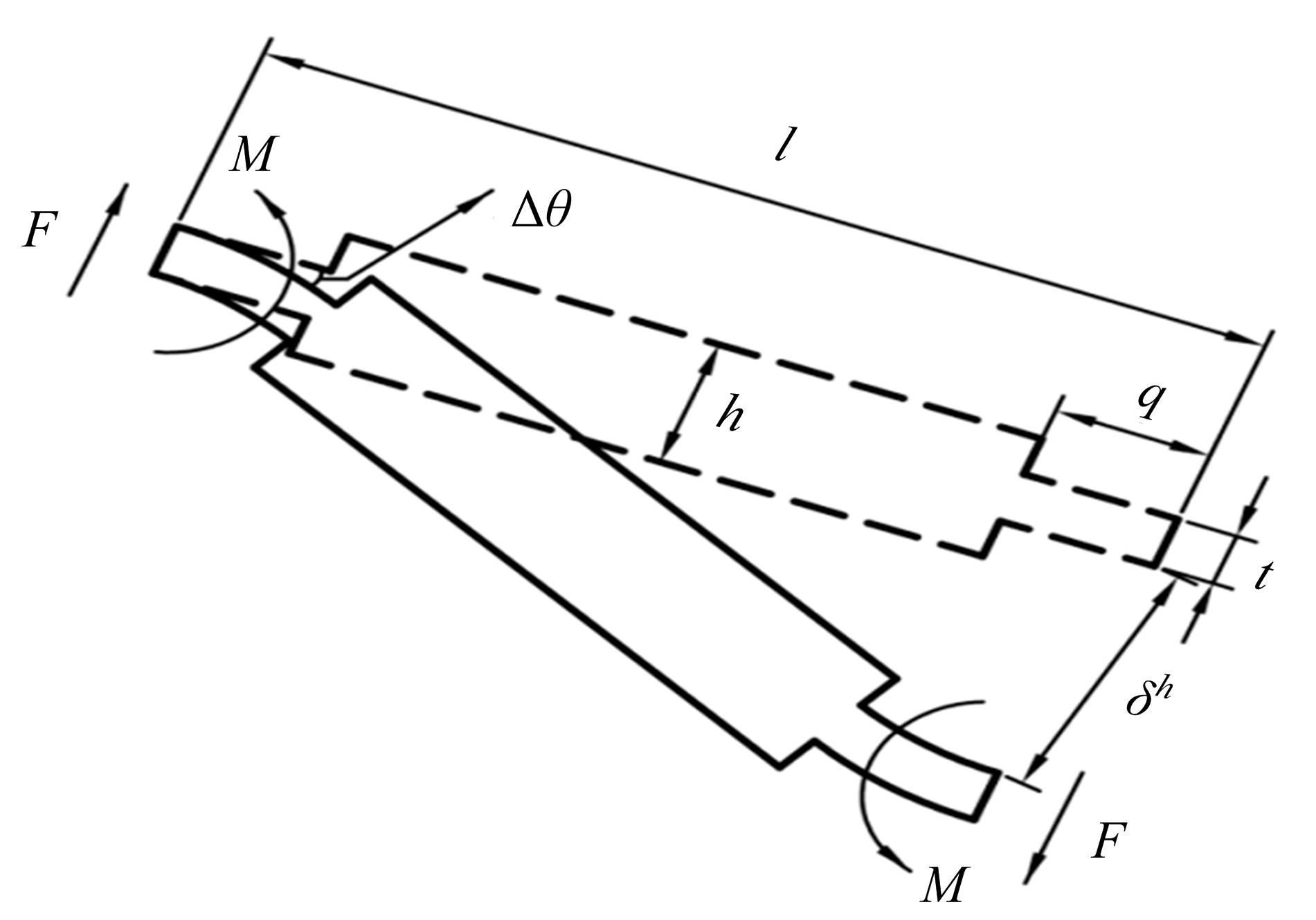
为探究铰接八面体结构的线压缩性与模型几何参数之间的内在关联，对该三维结构进行了有限元分析。在保证其他几何尺寸不变的前提下，通过改变杆长比l1/l2和杆件夹角θ1，建立了不同的有限元模型。具体讨论了杆长比和杆件夹角对该结构轴向线负压缩性（即NLC）大小和范围的影响。研究发现，通过合理地选择几何参数，该结构在3个轴线方向上均可存在线负压缩性，其中杆件夹角θ1的大小决定了线压缩性的正负，杆长比l1/l2的大小则决定了负压缩性的大小和存在范围。

关键词: 固体力学, 负压缩, 有限元法, 铰接八面体结构

Abstract:

In order to investigate the inherent link between the linear compressibility properties and the geometrical parameters, the 3D hinging octahedron structure was analyzed by a finite element method. With constant geometry size, different finite element models were established by changing the rod length ratio of l1/l2 and angle θ1 between the two rods. The effects of these two structure parameters on the magnitude as well as the range of negative linear compressibility (i.e. NLC) of this structure were analyzed and discussed. It is shown that through carefully choosing the geometry parameters, NLC can be exhibited in this model along the three?axis directions. More specifically, the sign of the linear compressibility is determined by the angle θ1 while the magnitude and range of NLC are determined by the l1/l2 ratio.

Key words: solid mechanics, negative compressibility, finite element method, hinging octahedron structure

中图分类号: 

  • O342

图1

理想铰接八面体结构及其各方向的投影"

图2

铰接八面体结构单胞有限元模型的几何尺寸"

图3

铰接八面体结构单方向加载示意图"

图4

铰接八面体结构线压缩性的理论结果与仿真结果对比"

图5

杆件柔性铰处的变形分析"

1 MorosinB, SchirberJ E. Linear compressibilities and the pressure dependence of the atomic positional parameter of As[J]. Solid State Communications, 1972, 10(3): 249⁃251.
2 SkeltonE F, FeldmanJ L, LiuC Y, et al. Study of the pressure⁃induced phase transition in paratellurite (TeO2)[J]. Physical Review B, 1976, 13(6): 2605⁃2613.
3 MariathasanJ W E, FingerL W, HazenR M. High⁃pressure behavior of LaNbO4[J]. Acta Crystallographica Section B: Structural Science, 1985, 41(3): 179⁃184.
4 FortesA D, SuardE, KnightK S. Negative linear compressibility and massive anisotropic thermal expansion in methanol monohydrate[J]. Science, 2011, 331(6018): 742⁃746.
5 BaughmanR H, StafstromS, CuiC, et al. Materials with negative compressibility in one or more dimensions[J]. Science, 1998, 279(5356): 1522⁃1524.
6 GrimaJ N, AttardD, Caruana⁃GauciR, et al. Negative linear compressibility of hexagonal honeycombs and related systems[J]. Scripta Materialia, 2011, 65(7): 565⁃568.
7 BarnesD L, MillerW, EvansK E, et al. Modelling negative linear compressibility in tetragonal beam structures[J]. Mechanics of Materialia, 2012, 46: 123⁃128.
8 GrimaJ N, Caruana⁃GauciR, WojciechowskiK W, et al. Smart hexagonal truss systems exhibiting negative compressibility through constrained angle stretching[J]. Smart Materials and Structures, 2013, 22(8): 84015.
9 GrimaJ N, AttardD, GattR. Truss⁃type systems exhibiting negative compressibility[J]. Physical Status Solidi, 2008, 245(11): 2405⁃2414.
10 ChoiJ B, LakesR S. Analysis of elastic modulus of conventional foams and of re⁃entrant foam materials with a negative Poisson's ratio[J]. International Journal of Mechanical Science, 1995, 37(1): 51⁃59.
11 ChoiJ B, LakesR S. Nonlinear analysis of the Poisson's ratio of negative Poisson's ratio foams[J]. Journal of Composite Materials, 1995, 29(1): 113⁃128.
12 LuZ X, LiuQ, YangZ Y. Predictions of Young's modulus and negative Poisson's atio of auxetic foams[J]. Physica Status Solidi B, 2011, 248: 167⁃174.
13 LiK, GaoX L, RoyA K. Micromechanics model for three⁃dimensional open⁃cell foams using a tetrakaidecahedral unit cell and Castigliano's second theorem[J]. Composites Science and Technology, 2003, 63(12): 1769⁃1781.
14 GrimaJ N, Caruana⁃GauciR, AttardD,et al. Three⁃dimensional cellular structures with negative Poisson's ratio and negative compressibility properties[J]. Proceedings of the Royal Society A: Mathematical Physical and Engineering Sciences, 2012, 468(2146): 3121⁃3138.
15 XieY M, YangX Y, ShenJ H et. al. Designing orthotropic materials for negative or zero compressibility[J]. International Journal of Solids and Structures, 2014, 51(23/24): 4038⁃4051.
16 ZhouX Q, ZhangL, ZhangH, et al. 3D cellular models with negative compressibility through the wine⁃rack⁃type mechanism: 3D cellular models with negative compressibility[J]. Physica Status Solidi, 2016, 253(10): 1977⁃1993.
17 MastersI G, EvansK E. Models for the elastic deformation of honeycombs[J]. Composite Structures, 1996, 35: 403⁃422.
[1] 刘程, 史文库, 陈志勇, 何伟, 荣如松, 宋怀兰. 汽车驱动桥准双曲面齿轮齿根弯曲应力预测与试验[J]. 吉林大学学报(工学版), 2017, 47(2): 344-352.
[2] 闫光, 庄炜, 刘锋, 祝连庆. 具有增敏效果的光纤光栅应变传感器的预紧封装及传感特性[J]. 吉林大学学报(工学版), 2016, 46(5): 1739-1745.
[3] 胡玉明, 黄音, 古海东. 排桩支护结构内力与变形三维有限元数值分析[J]. 吉林大学学报(工学版), 2016, 46(2): 445-450.
[4] 肖湘， 黄恩厚， 尼颖升. 预应力混凝土梁板体系有效翼缘的理论分析及试验[J]. 吉林大学学报(工学版), 2015, 45(6): 1784-1790.
[5] 庄蔚敏, 解东旋, 余天明, 于皖东. 基于损伤-相变本构模型的高强钢热成形数值模拟分析[J]. 吉林大学学报(工学版), 2015, 45(4): 1206-1212.
[6] 孟广伟，李霄琳，李锋，周立明，王晖. 裂隙介质渗流的光滑多尺度有限元法[J]. 吉林大学学报(工学版), 2015, 45(2): 481-486.
[7] 马彪1, 赵家昕1, 李和言1, 宁克炎2, 何春平3. 离合器结构参数对其热弹性不稳定性的影响[J]. 吉林大学学报(工学版), 2014, 44(4): 933-938.
[8] 李晓军,梁路路,谢诚伟,杨硕. 沥青混凝土虚拟力学仿真模型自动生成及应用[J]. 吉林大学学报(工学版), 2014, 44(3): 655-660.
[9] 庄蔚敏, 曹德闯, 叶辉. 基于连续介质损伤力学预测7075铝合金热冲压成形极限图[J]. 吉林大学学报(工学版), 2014, 44(2): 409-414.
[10] 彭勇, 孙立军. 集料水平向分布状态对沥青混合料劈裂试验影响数值模拟[J]. 吉林大学学报(工学版), 2013, 43(04): 891-896.
[11] 张强, 张璐, 刘宪军, 于路路, 贾洪雷. 基于有限元法的仿生钩形深松铲耕作阻力[J]. 吉林大学学报(工学版), 2012, 42(增刊1): 117-121.
[12] 邓兆祥, 高书娜. 结构声腔耦合系统的振型耦合特性分析及应用[J]. , 2012, 42(05): 1120-1126.
[13] 庄蔚敏, 陈延红. 基于连续损伤力学的表面涂层损伤模拟[J]. , 2012, 42(04): 857-862.
[14] 闫清东, 崔红伟, 魏巍. 新型液力变矩减速装置变矩工况叶轮有限元强度分析[J]. 吉林大学学报(工学版), 2012, 42(02): 365-371.
[15] 孙钟雷, 孙永海, 方旭君, 刘晶晶. 仿齿冠压头破碎物料试验及模拟[J]. 吉林大学学报(工学版), 2011, 41(增刊2): 236-240.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
版权所有 © 《吉林大学学报(工学版)》编辑部
地址：长春市人民大街5988号　电话：+86-431-85095297　传真：+86-431-85094074　E-mail: xbgxb@jlu.edu.cn
本系统由北京玛格泰克科技发展有限公司设计开发