�����������澫��ʱ,�ܲ����ɱ���Ч�ʵ�Ӱ��,�����������������ܹ������ʹ���IJ����㾡����ȫ��̻������������������������еĹؼ����ܼӹ��������ܵ�Ӱ��,����������������,���ʴ�IJ�λ�������ڽϴ�ļӹ����,��͵����˲�����Ӧ���������������Ӧ�ֲ������õIJ��������о��Ȳ���������������������Ȳ���ֻ���ڲ�������Ŀ�㹻���ǰ���²��ܷ�ӳ���������ʵ����,���϶�IJ�����ή�Ͳ���Ч��;����������Žϴ������,��ĿǰΪֹû���γ�ͳһ�IJ�����[1];���е�Hammersley��Halton���в��������Ч�ؽ��Ͳ����ܶ�ȴ����ʵ�����������Ӧ����[2,3]�������һ����������������ڶ�ѧ�߶���������������Ӧ�ֲ�����˶��ַ����������д����Ե���Li[4]������������ʲ������Ӧ�滮����,�������[5]��������������һ��ȷ�����ʲ�ȵķ���,ʵ���˸������������µ�����Ӧ����;Zhang��[6]����������IJ�ͬ��������������ȡ,���ø�˹ӳ��õ��˿��з���,�Ӷ��滮������·��,�����˻��������ļ��ϵͳ;Elkott��[7,8]���������Ȳ������߲�������,���õõ��IJ������ع�����ļ�����״,�������ֻ������ߵ�������������������������������Ϣ�Ķ�ʧ;Hu��[9]�����һ�ֻ������ߵĵȻ�������,���ַ���Ҳ���������������Ϣ�Ķ�ʧ,���ҽ���������ijЩ�����¶ȵ�����,������һ����;Suleiman��[10]���������滮��Ϊ��������,�ڸ������ڷֱ��ҳ����������С��˹���ʺ�ƽ�����ʵĵ���ʵ�����������Ӧ����,��ȱ���Dz������ڴ�С���ʴ����ּ���,����ȫ��ؿ̻�������ṹ;����������Voronoi�ṹ���������֡�ͼ�����Ż���Դ���䡢��������ȷ����Ӧ��Խ��Խ��[11,12],��ȡ����һ���ijɹ�,��������[13]��������Voronoi�ṹ�����Ӧ��ֵ�����������ɢ,֤���˸÷��������㷽��Ŀɿ��ԡ�
��������������Voronoi�ṹ���ŵ�,��������������������ʺ����������뼸������,�����һ���µ�������������Ӧ�����㷨��
����һ��������RN,������{Vi}ki=1����Vi��Vj=��(i��j),�����Ϊ����һ���ṹ,ȡ������2ΪRN�е�ŷʽ����,��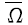 �е�һ���{zi}ki=1,����zi���Ӧ��Voronoi����Ϊ
�е�һ���{zi}ki=1,����zi���Ӧ��Voronoi����Ϊ
Voronoi�ṹҲ������һ���������ڵ�ֱ�߶εĴ�ֱƽ������ɵ���������ι��ɡ���֪����Ԫ������Ϊzi(xi,yi)��zj(xj,yj),���ݽ������ε�֪ʶ����䴹ֱƽ���ߵķ���Ϊ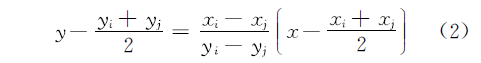
��������V��RN��һ��������V�ϵ��ܶȺ�����,��������V������z*Ϊ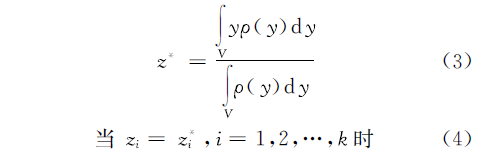
��Voronoi���� �ķ���Ԫ���������غ�,�������ĽṹΪ����Voronoi�ṹ�����ijɱ���������Ϊ
�ķ���Ԫ���������غ�,�������ĽṹΪ����Voronoi�ṹ�����ijɱ���������Ϊ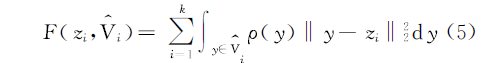
��������Ļ���Ϊ���ܶȺ������µ�����Voronoi�ṹʱ,������ijɱ������ڸ��ܶȺ����´ﵽ��Сֵ,��ͼ1��ʾ��
.
 | ͼ1 ����Voronoi�ṹFig.1 Centroidal Voronoi tessellation |
��֪��������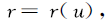 ���俴��һ�����������������ֲ������ȵ�����,�������ʺ�����Ϊ�����ߵ��ܶȺ���,ʽ(6)Ϊ���ʺ������ʽ��
���俴��һ�����������������ֲ������ȵ�����,�������ʺ�����Ϊ�����ߵ��ܶȺ���,ʽ(6)Ϊ���ʺ������ʽ��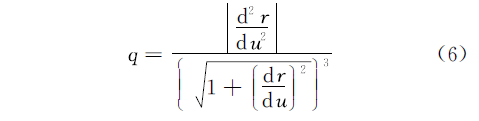
����ʽ(6)��֪,���ʺ�������,���䲢���⻬�������ʽ(6)���ʵ�����,ʹ����Ҫ��Χ�ڳ�Ϊ�⻬����ֵ����,��Ϊ��ʽ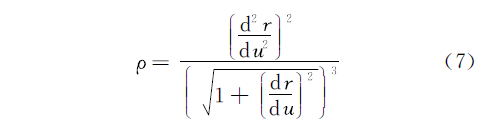
�Ϳ���������������Voronoi�ṹ�����ж��ܶȺ�����Ҫ��,����[14]��֤��,��һά�����,����ijɱ�������ȫ��������,���Կ���������Ϊ�㷨���������ݡ�ʵ����������Ӧ������㷨��������:.
Step1 ������������ֲ���������Ϊ��ʼ��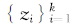 ,������С�ڲ�����Ŀ,�Գ�ʼ��Ϊ��������ʽ(2)��������Ϊ��Ӧ��Voronoi����
,������С�ڲ�����Ŀ,�Գ�ʼ��Ϊ��������ʽ(2)��������Ϊ��Ӧ��Voronoi����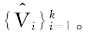 .
.
Step2 ����ʽ(3)���������������ġ�
Step3 �ڸ�������������ʽ(5)�����������ߵijɱ�����,�������Ƿ�����,��������ֹͣ,������������ļ���Ϊ���������,����������Ϊ�µij�ʼ��ת��Step2��
Step4 �ڵ�����������,�ھ���������������֮��(��Ϊƽ̹������)���Ӳ�����,ֱ������ʵ��Ͳ�������������Ҫ��,��������㡣
������Ϸ���,��������˷���ʵ���Լ��������㷨�Ƿ���Ч��ȡ��������r(u)=sin(u)-u2/16,ͼ2Ϊ��5�ε���������IJ���Ч��,��ͬһ���������þ��Ȳ������㡢�Ȼ��������������ֳ��õķ����ɼ���ͬ��Ŀ�IJ��,����ͬһ�ַ������в�ֵ,ͼ3Ϊ���ַ�����ϳɵ�������ԭ���ߵĶԱȡ����Կ����������㷨�õ��IJ������ڿ̻�������״����ȳ��õķ���ȡ���˸��õ�Ч��,�ܹ���ʵ��Ӧ�������״,�ر��������ʽϴ�ĵط���ͼ4����1��ʾ�˲�ֵ������ԭ���ߵķ���ƫ�
.
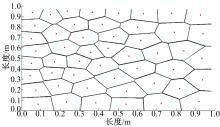
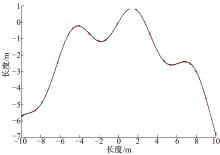 | ͼ2 ���ֲ�ʾ��ͼFig.2 Sampling points distribution |
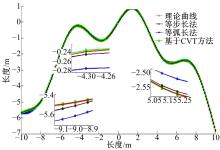 | ͼ3 ������϶Ա�ʾ��ͼFig.3 Comparison of three interpolated curves |
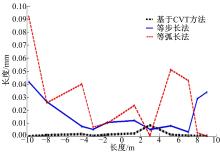 | ͼ4 ����ƫ��Ա�ͼFig.4 Comparison of normal deviation |
| ��1 ��ͬ������������Ա�Table 1 Comparison of fitting error by different methods |
���������㷨�����߲���������ֳ�������Ч��,���ǴӶ�ά������ֲ����ά���ڽ������ɵ�����⡣�ɵ�2�ڵ�����֪,�ﵽ��ֲĿ�ص�ǰ������Ҫ�ҵ����ܷ�Ӧ�������ʱ仯�ֿ�����Ϊ�ܶȺ������º���,��֮��������Voronoi�ṹ,����ɱ����������ּ��ε�֪ʶ֪,����ĸ�˹���ʵľ���ֵ��ʾ���Ǹõ㼰���ڽ���ĸ�˹ӳ����ɵ�����Ƭ����*�������ԭ����Ƭ���ҵ����֮�ȡ������ҡ�0,�������ɸõ�ļ���ʱ,�����ֵ���Ǹõ�ĸ�˹���ʡ���Ӧ�������ڸõ㴦�������̶ȡ�������IJ������ʽΪS=S(u,v),���˹���ʵı��ʽΪ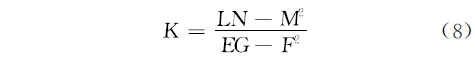
ʽ��: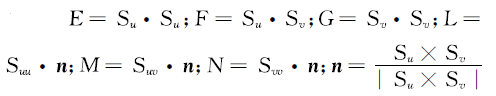 �Ǵ�������ĵ�λ��������
�Ǵ�������ĵ�λ��������
�����������������涼�м�������ѧ���ʽ,������ɢ��ʽ������-ϸ�����桢�������桢��������,������һ����STL��ʽ�������洢����,���ּ����е�Gauss-Bonnet����,���Զ���ɢ����и�˹���ʵĹ���,����pi�������ΪAM��������Gauss���ʵĻ��ֱ��ʽΪ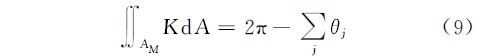
�Ի��ֽ�����ɢ,�õ���˹���ʵ���ɢ��ʽΪ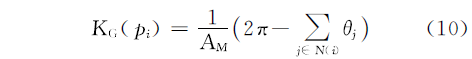
ʽ��:KG(pi)Ϊpi�����ĸ�˹����;��j��ʾ������Ƭ�б�pipj���pipj-1�ļн�;AMΪ����pi���������,�˴�����Voronoi��������㡣
ͨ������������Voronoi�ṹ�Ĺ��̽��з���,����������IJ����������Ҫ�õ��������,����Voronoi��������,����ػ��ֵļ�������ܴ������,ͬʱ�����ܱ�֤��˹���ʺ����Ĺ�˳�ԡ�Ϊ�����һ����,���Ľ�����ͶӰ������ɢ,ѡ��һ�����ε�ƽ��,���Ը������ű�������,��������任ʹ������ƽ����ͬһ����ռ���,������ÿһ���㶼ͶӰ������������,����������ÿһ��Ҳ������,���������ϵ�ͶӰ��,���ʵ���ԭ�����϶�Ӧ��ĸ�˹���ʾ���ֵ,����ȡΪ����,�������бߴ�����,����ʵ�����������ڵIJ���,����������ֵļ�������,�������¶�������������Voronoi�ṹ�������õ���������ĵĹ�ʽ�ͼ�������ɱ������Ĺ�ʽ: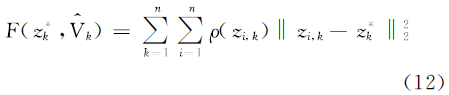
ʽ��: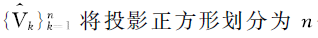 ��Voronoi����;
��Voronoi����;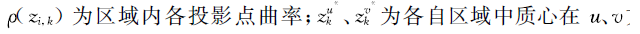 ��������ꡣ
��������ꡣ
ʽ(12)Ϊ�������ڵijɱ�����,������[12]��֪,�ڶ�ά�����,�ɱ������Ǿֲ�������,�����Խ�����Ϊ�ж��㷨��������������ı߽��������������߲�����㷨,���������������IJ���,�㷨����ͼ��ͼ5��ʾ��
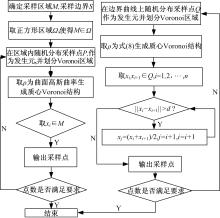 | ͼ5 �����㷨����ͼFig.5 Flow chart of proposed algorithm |
������Ϸ���,��������˷���ʵ���Լ����㷨����Ч��,ȡ��������,s=sin(u)+sin(v),u,v��[0,1],�ٶ�������Ϊ80��,ͼ6Ϊ����CVT��������������������������Ӧ�ֲ���ʾ��ͼ,����������ɱ�������432.5������123.2,�ɱ�����������71.5%����ͼ6���Կ�������IJ�����������������Ӧ�ֲ�,��Matlab2011�е�������Ϲ�����,��������������Ȳ���������CVT���������õ��IJ����ͬһ�ַ��������������,�������2��ʾ,����2��SSE��ʾ���������ԭʼ���ݶ�Ӧ������ƽ����,��Խ�ӽ���0˵���������Ч��Խ�á�RMES��ʾSSE��ֵ��ƽ������R-square��ʾȷ��ϵ��,��Խ�ӽ���1˵�����Ч��Խ���롣���Դ���2�ɿ����ñ��ķ����õ��IJ�������ϳ���������ԭ������ӽ�,�õ��IJ��������ȷ��ӳ�����������״��Ϣ��
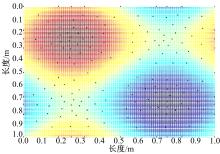 | ͼ6 ����ʾ��ͼFig.6 Schematic diagram of sampling |
| ��2 ���ַ����������Ч���Ա�Table 2 Effect comparison of fitting surface by three methods |
(1)���ķ������Խ������ط�Ӧ�������������������Ϣ,�������������û����߲�������ʱ������Ϣ�Ķ�ʧ��
(2)���ķ�������������,������ѧ���ʽ����������Ҳ���á�
(3)�õ��IJ������ܸ���ȷ�ؿ̻�������״,Ϊ������������������ṩ��������֧�֡�
(4)Ϊ�����㷨��д����Ӧ�ij���,����˷���ʵ��,���뼸�ֳ��õIJ�����Խ����˱Ƚ�,ʵ��������ķ�����ʮ����Ч�ġ�
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|

