申桂香(1957),女,教授,博士生导师.研究方向:数控装备及其全生命周期工程.E-mail:shengx@jlu.edu.cn
讨论了由几个相互独立的子系统组成的串联系统的寿命服从两参数威布尔分布时,其子系统的可靠性建模问题。并指出当某子系统出现故障时,其他子系统故障数据按照截尾数据处理,然后用平均秩次法对故障顺序修正,据此进行模型参数估计和拟合性检验,可以达到减小建模误差、提高拟合精度的目的。最后以某加工中心现场试验数据为例介绍该方法的具体应用过程,以验证该方法的有效性和实用性。
This paper presents a method of the reliability modeling of a series system. Such a system is composed of several mutual independent subsystems, and the system life-time obeys two-parameter Weibull distribution. In this method, when one of subsystems is failure, the fault data of the other subsystems are processed as censored data, and the failure sequence is revised using the average rank time method. This method can be applied for model parameter estimation and fitting test to reduce the modeling error and improve the accuracy. Finally, as a case study, the real data of a Computerized Numerical Control (CNC) are used to demonstrate the application of the proposed method, which verifies the effectiveness and applicability of the method.
可靠性模型是可靠性评价、预测等可靠性研究的基础,其合理与否直接影响其他可靠性工作的正常进行,因此,可靠性建模是可靠性工作中的重中之重。迄今为止,已有很多人对可靠性建模方法进行研究,主要集中在可修系统与不可修系统,串联系统、并联系统、表决系统与冗余系统等系统级可靠性建模方面[ 1]。目前也有人从系统组件和系统结构角度提出基于分治法思想的系统可靠性建模方法[ 2]和利用Petri网模型进行基于随机故障序列分析的系统动态可靠性建模研究等[ 3, 4, 5]。系统的可靠性水平由其各子系统的可靠性水平和系统结构决定[ 6],但如何描述并评价系统运行中各子系统的可靠性却是一个值得研究的问题。
为节约时间和成本,系统可靠性试验多为定时截尾寿命试验,所得到的数据包含大量截尾数据。当系统发生故障时,一个组件会产生一个自身的故障时间,并使得所有其他组件的时间截尾[ 7]。因为系统其余组件故障截尾数据的存在,使故障数据的次序发生变化,如何修正这种变化是可靠性建模的关键。
本文主要讨论由相互独立的子系统组成的串联可修系统在运行中其子系统可靠性建模问题。考虑到截尾试验与组件故障引起的截尾数据的影响,应用平均秩次法实现对故障顺序号的修正,采用中位秩法计算经验分布函数,用最小二乘法进行参数估计,用d检验法进行拟和性检验得到子系统可靠度模型。通过相关指数将采用该方法得到的串联系统可靠度模型与不考虑组件故障的串联系统可靠度模型、直接参数估计得到的可靠度模型进行对比,以验证本文方法的合理性与有效性。最后,以6台某系列加工中心截尾试验得到的18个故障数据为例[ 8],介绍具体应用过程。
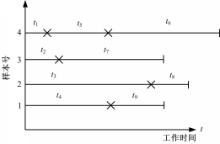
目前许多产品都采用定时截尾试验方式进行试验,但由于各试验样本投入使用的时间不一定相同,虽然试验截止时间相同,也导致数据出现随机截尾的特性,这种随机截尾称为随机逐次截尾[ 9]。在随机逐次截尾试验时,既会因试验截尾产生截尾数据,也会因组件故障产生截尾数据,故属于多重截尾数据。试验数据的特点可用图1表示。
由图1可知,4个试验样本共出现5个故障数据 t1 、 t2 、 t3 、 t4 、 t5,4个截尾数据 t6 、 t7 、 t8 、 t9,为与故障数据相区别,截尾数据后面加上“+”,将这9个数据按照增序排列得: t1< t2< t8+< t5 < t9+< t4< t6 +< t7+< t3 。因为 t8是一个截尾数据,这将会影响数据 t5的故障顺序,所以 t5的故障顺序不能只按故障数据排序定为3,也不能按总体排序定为4,而是一个介于3与4之间的数值。
因截尾产品既有可能在下一个故障之前出现故障,也有可能在其之后出现故障,所以这将会影响随后故障的秩。为此,Johnson给出了多重截尾数据估计 F( ti)与 R( ti)的方法,该方法是通过调整数据秩后,再根据中位秩法计算的。
设试验产品数为 N , 
秩增量 
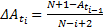 | (1) |
式中: 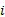
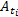
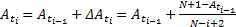 | (2) |
有了平均秩次,即可带入近似中位秩公式中计算产品的经验分布函数:
 | (3) |
参考文献[ 8],6台某加工中心故障数据,根据故障分析结果,将其分为机械系统、电气系统和辅助装置三类子系统故障,具体见表1。将各类故障分别整理,得到三类子系统故障数据见表2。
| 表1 加工中心故障记录汇总表 Table 1 CNC fault recording summaries |
| 表2 加工中心子系统故障数据表 Table 2 CNC subsystems fault data |
| 表3 加工中心故障间隔时间数据表 Table 3 Time between failures(TBF)of CNC data |
假设加工中心故障数据服从二参数威布尔分布,根据文献[ 9]的方法,其参数估计过程见表4,采用最小二乘法得到参数估计值,经线性相关性检验和d检验发现数据服从假设分布,故可靠度模型为

| 表4 基于平均秩次法的故障分布函数估计 Table 4 Fault estimation of distribution function based on average rank time method |
以机械系统为例,共有5个故障数据,其余13个为因其他子系统故障引起的截尾数据,另有6个因试验引起的加工中心截尾数据,基于平均秩次法得到各故障数据的秩次,具体如表5所示。为区别,截尾数据后面加上“+”。假设故障数据服从威布尔分布模型,基于平均秩次法的3个子系统故障分布函数参数估计值见表6。
| 表5 基于平均秩次法的机械系统故障数据秩次 Table 5 Mechanical system fault data rank based on average rank time method |
| 表6 子系统威布尔分布模型的参数估计和相关系数 Table 6 Parameter estimation and correlation coefficient of subsystem Weibull distribution model |
参考文献[ 7],当 α=0.1, n=24时, D n,α=0.138, ρ n,α=0.3383。由表6数据可知,子系统故障数据服从假设的威布尔分布模型。
以机械系统为例,不考虑其余子系统故障,根据表2可以直接计算其故障间隔时间数据和截尾数据为
30,168,82,276,8,484+,709+,524+,90+,782.5+,1234.5+
假设故障数据服从两参数威布尔分布,采用最小二乘法进行参数估计,采用线性相关系数法和d检验法进行拟合性检验,可以计算得到各子系统可靠性模型分别为
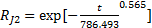 | (4) |
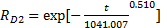 | (5) |
 | (6) |
加工中心任一子系统出现故障都会引起系统故障,故加工中心可看作串联系统:

由表6和式(4)(5)(6)可得系统可靠度函数 R串联1 、 R串联2 。
为定量评价拟合效果,本文参考文献[ 10],采用相关指数 k来衡量:
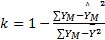 | (7) |
式中: Y M为故障分布函数真值,由中位秩公式计算得到; 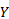

由式(7)计算得到的 k∈(0,1), k值越接近1,说明曲线拟合得越好,数据遵从所假设分布的程度越高。
根据故障数据,计算得到系统可靠度函数对数据的拟合程度分别为 k拟合=0.988, k串联1=0.932, k串联2=0.830。
由此可以发现,按考虑其余子系统故障,运用平均秩次法进行数据修正计算子系统可靠性模型后,再按系统串联得到的可靠度函数与直接对系统进行可靠性建模得到的函数,拟和效果基本一致,所以,据此进行子系统可靠度计算应更合理、更符合实际。
(1)考虑其余子系统故障,用平均秩次法对故障数据顺序号进行修正后,能够解决多重截尾数据与故障数据并存时的产品可靠性建模问题。
(2)由优度检验相关指数值可知,考虑其余子系统故障,采用平均秩次法计算子系统可靠性模型后得到系统串联模型,与对故障数据直接拟合得到系统可靠度模型与真值的拟和度均大于0.9,且趋于相等,用两种方法得到的可靠度分布函数曲线与真值曲线的接近程度都较高。这说明,考虑其余子系统故障,按平均秩次法计算子系统可靠性模型是符合实际、合理的。
(3)考虑其余子系统故障,采用平均秩次法既考虑试验截尾时间,也考虑组件截尾时间,据此对故障数据顺序号进行修正,此方法原理清晰,计算过程方便简洁,避免了复杂的编程计算和繁琐的推导,而且结果精确度相对较高,故本文方法具有一定的理论意义和应用价值。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|