吕锋(1980),男,讲师,博士研究生.研究方向:农业系统工程.E-mail:lvfeng1980@126.com
针对设备重要度概念的模糊性和评价指标的多样性特点,以及均一评价方法对不同的评价对象采用相同的权重分配,不能体现评价最优性的不足,提出了一种基于欧氏贴近度的改进模糊物元模型的设备重要度评价新方法。该方法依据Pareto原则,综合向量余弦的灰关联和DEA确定指标权重,采用模糊物元模型计算各设备的重要度,对设备重要程度进行评价与排序,并以某农机企业生产线的7台设备进行实证研究。结果表明,该方法避免了由于主观判断而导致权重的不确定性,提高了方案之间的可区分性,比传统方法更具优势。
The concept of equipment criticality has the characteristics of fuzziness and diversity of evaluation index. Uniform evaluation method uses the same weight assignment for different evaluation objects, which does not reflect the optimality of evaluation. To overcome this problem, a new method for equipment criticality evaluation is put forward based on fuzzy matter-element analysis, combing with the concept of Euclid approach degree. The method integrates grey relation analysis based on the cosine distance and data envelopment analysis in a unified way to determine the index weight according to Pareto rule. The fuzzy matter-element model is applied to compute the equipment criticality, thus the grade classification of equipment criticality is obtained. Then, as a case study, experiment on seven equipments in a production line of an agro-machinery enterprise is carried out. The results show that the method can avoid the uncertainty in estimating the weights subjectively, increase the basic discrimination in the evaluation, so it outperforms the available traditional methods.
设备重要度是指不同种类的设备在设备保障工作中所处地位的重要程度。企业为了使设备完好、正常地运行,延长设备的使用寿命,需要在设备的重要度评价基础之上进行科学、合理、有效的设备保障工作,以减小维修的盲目性,提高设备的可用性并降低运行、维修费用。影响设备重要度的因素很多,而且这些因素对其影响不同,难以用同一标准来衡量。同时,影响因素及标准本身都具有模糊性,因此用经典数学方法难以解决。现有设备重要度评价方法有ABC分析[ 1]、BP神经网络[ 2]、可拓理论[ 3]、TOPSIS[ 4]、蒙特卡洛模拟[ 5]、模糊综合评判[ 6]、模糊聚类分析[ 7]等,这些方法在实际工作得到了一定程度的应用。但是,以上评价方法分别从主观或客观方面对设备重要度进行评价。主观评价难以避免主观因素的影响;客观评价计算结果可能与实际情况不符。同时,存在需要主观参数多,计算复杂等缺点[ 8]。而且,在属性较多时,加大了决策者评判的难度,可能导致不能真实反映他们的意见[ 9]。
鉴于此,本文针对设备重要度评价因素的不确定性及信息的有限性,提出利用物元分析的理念,结合模糊集和贴近度的概念,建立设备重要度综合评价模型。该方法综合了模糊物元、灰关联和DEA的优势,通过均一和非均一综合赋权,既克服了确定权重时的主观性,又兼顾了优先序评价的最优性和公正性,从而为设备重要度评价提供一条可行的新途径。
在一个多目标决策方案中,将事物、特征以及量值以有序三元组来描述[ 10, 11, 12]。事物即方案Mj,表示第j个方案;特征即评价指标Ci表示第j个方案的第i项评价指标,其对应的量值用xji表示,从而可以构成以Rmn表示的m个方案的n维复合物元。
将xji量值改为模糊物元量值,则称为m个方案n维复合模糊物元,即:
 | (1) |
式中:μ ji表示第j个方案第i个评价指标相应的从优隶属度。
越大越优型: 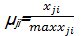
越小越优型: 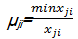
其中, j=1,…, m; i=1,…, n;max x ji,min x ji分别表示 R mn中 x ji的最大值和最小值。
由式(1)可以构成标准样品 M0的 n维模糊物元 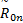
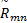
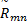
以 R w表示每一方案各评价指标的权重复合物元,并以 W i *表示每一方案第 i项指标的组合权重。
利用基于 Pareto原则的灰关联和 DEA确定组合权重,可以计算得到 R w,即:
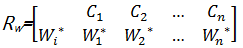 | (2) |
1.2.1 灰关联确定指标权重
各评价指标的权重可应用向量余弦的灰关联进行确定。
(1)评价矩阵生成
设指标体系共有m项指标,有n个方案,则评价矩阵为 X=( x ij) m×n( i=1,2,…, m; j=1,2,…, n),其中 x ij表示第 j个方案关于第 i个评价指标的指标值。
(2)参考序列选取
最优序列 U和最劣序列 L,其中 U=( u1, u2,…, u m)T, L=( l1, l2,…, l m)T。对越大越优型指标,最优序列 U取大,最劣序列 L取小,反之,对越小越优型指标, U取小, L取大。
(3)各方案与 U、 L的相对偏差矩阵确定
优偏差矩阵R=(rij)m×n;劣偏差矩阵S=(Sij)m×n。
式中:
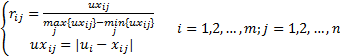 | (3) |
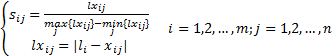 | (4) |
(4)各评价指标权重的确定
计算 R的行向量 r i与 S对应的行向量 s i的余弦夹角[ 13]:
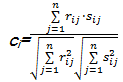 | (5) |
得 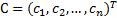
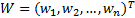 | (6) |
式中: 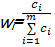
1.2.2 用 DEA确定指标权重
DEA对每一个决策单元建立对其最有利的数学规划模型,通过解其最优解来确定指标权重,不同的决策单元拥有不同的指标权重,且均相对最优。因此, DEA是一种变权评价方法,属于非均一评价[ 14]。本文为了尽最大可能避免由于指标取舍与简化带来的影响,采用仅有产出的多目标 DEA模型[ 15]。
设有 n个决策单元 DMU j( j=1,2,…, n),仅知其产出为:
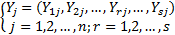
式中: Y rj表示第 j个决策单元 DMU j的第 r种产出。
建立仅有产出的多目标 DEA模型为
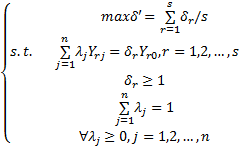 | (7) |
求解上述线性规划模型即可得各指标相应的权重,将其归一化处理,可得:
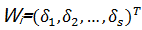
1.2.3 综合权重的确定
灰关联为均一评价方法, DEA是非均一评价方法,本文依据 Pareto原则[ 16],采用线性加权方法确定评价指标的综合权重,即:
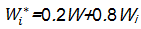 | (8) |
用欧式贴近度表示所给样本与标准样本之间的贴近程度,即:
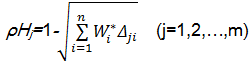
由此,构造样品欧式贴近度复合模糊物元:
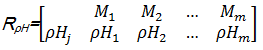 | (9) |
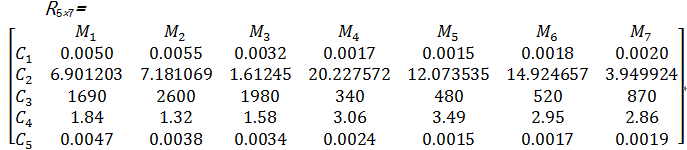
本文选取某农机企业同一生产线的7台设备进行研究[ 17],所得基础数据如表1所示。
| 表1 某农机企业生产线设备基础数据 Table 1 The basic data of product line equipment |
构造复合物元 R5 ×7。加工精度要求 C1,资产原值 C2,年平均停台时间 C3,年平均维修费用 C4和平均故障间隔时间倒数 C5均为越大越优型即产出指标。根据从优隶属度,可得复合模糊物元 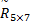
(1)最优与最劣向量确定
最优向量:
U=(0.0055,20.227572,2600,3.49,0.0047)T
最劣向量:
L=(0.0015,1.61245,340,1.32,0.0015)T
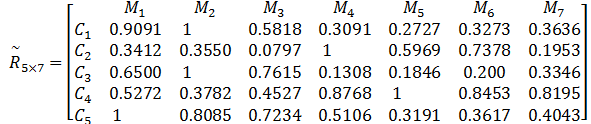

(2)权重确定
各方案与 U, L的相对偏差矩阵 R, Δ为


R, Δ是根据确定的最优向量和最劣向量而得。由式(5)(6)知各指标的权重 W为
W=(0.1383,0.2589,0.1879,0.2080,0.2069)T
采用线性比例法对指标原始数据进行无量纲化处理,可得矩阵 B。
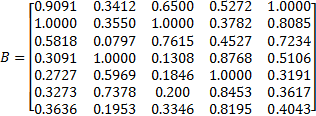
针对设备 A,应用 Matlab软件求解规划(7),可得: δ'1=1, δ1=1.0000, δ2=1.0000, δ3=1.0000, δ4=1.0000, δ5=1.0000.
对其归一化处理可得:
W1=(0.2000,0.2000,0.2000,0.2000,0.2000)T
同理:

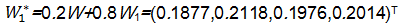
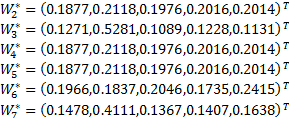

根据欧式贴近度的大小可以确定设备的重要顺序为: M1、 M2、 M4、 M6、 M5、 M7、 M3。
在模糊物元分析的基础上,结合各待评价方案与理想解之间的欧式贴近度,建立了欧式贴近度复合模糊物元,通过基于 Pareto原则的灰关联和 DEA确定组合权重,既避免了由于主观判断而导致权重的不确定性,又提高了方案之间的可区分性,能够全面客观地反映出各评价指标的重要性,使评价结果更加客观、合理,为企业设备重要度评价提供了一种新的途径。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|


