温涛(1962),男,教授.研究方向:服务计算,网络安全.E-mail:wentao@neusoft.edu.cn
针对有QoS保障的组合服务选择中,Web服务的QoS难以精确测量以及用户的QoS需求难以准确表达的问题,提出了一种不确定信息下服务选择的新方法,该方法采用区间数的形式描述用户的QoS需求以及服务的QoS指标,引入组合服务用户满意度评价,基于带有动态边界的改进粒子群算法寻找满足用户全局QoS需求的Web服务组合方案。实验结果表明,该方法有效可行。
In Quality of Service (QoS)-guaranteed composite Web service selection, it is difficult to obtain the accurate measurements of QoS. Meanwhile, users' QoS requirements are hard to describe. To address these concerns, a novel method of Web service selection is proposed. It uses interval numbers to describe users' QoS requirements and QoS metrics of Web services, and introduces user satisfaction degree to evaluate the composite services. Base on a Particle Swarm Optimization with Dynamic Boundary (DBPSO), the method tries to find appropriate composite service scheme that meets the users' global QoS requirements. Simulation results show that the proposed method is both feasible and effective.
Web服务具有跨平台、异构、松散耦合等特点,逐渐发展成为互联网上一种重要的分布式计算模式。实际应用中,为满足用户复杂的需求,通常需要基于特定的业务流程模型,动态发现已存在的Web服务,并组装成一个更大粒度的服务,以实现完整的业务逻辑。在Web环境中,不同的服务提供方提供了大量功能相同或相似而QoS指标(如执行时间、价格等)不同的Web服务,如何能够动态地从中选择既满足功能需求,也满足用户全局QoS约束的服务进行组合已经成为一个亟待解决的问题。对于有QoS保障的服务选择问题已经有了很多研究成果[ 1, 2, 3]。但是大部分工作都使用历史日志的期望来近似实际的QoS值,并将其作为确定值在UDDI上发布。虽然假设QoS是确定的数值可以简化计算工作,但在实际应用中却有很大的限制。例如,任何服务调用的响应时间都依赖于这样一个非确定性的因素,即同一时刻调用的任务数,显然,任务数越多,服务调用的响应时间就越长,同时,响应时间还会受到网络状态的影响。正是由于Web服务实际执行环境中的诸多不确定性因素共同影响着Web服务,从而导致其QoS不可避免地会产生变化。因此,在研究Web服务选择问题时,充分考虑QoS的不确定性有着重要的现实意义。
文献[ 4]考虑到影响服务QoS度量的不确定因素,将Web服务的各项QoS指标定义为一系列随机变量,并利用随机变量的数学期望和方差来度量各属性,基于马尔科夫决策过程设计了随机QoS感知的可靠Web服务组合算法。文献[ 5]提出了Web服务QoS的概率模型,将QoS指标建模为离散型随机变量,每个QoS指标的概率密度函数指明了QoS取某些特定值的概率,同时,给出了基于样本空间消减的QoS聚合算法,采用启发式贪心方法搜索组合方案。目前,就研究不确定问题而言,概率模型[ 6]和模糊模型[ 7]是处理该类问题的两种较为常用的模型,但无论是随机过程的分布函数,还是模糊数学的隶属函数往往都不易确定,因此有些学者试图使用非概率理论解决不确定问题,区间分析方法[ 8, 9, 10]是近年得到较快发展的一种处理不确定问题的方法,它利用区间描述不确定性参数,符合人的思维习惯,表示形式简单,无需太多的先验知识,因此在不确定性建模方面具有较好的方便性和经济性。近年来,也有学者基于区间型的QoS讨论服务组合和选择问题。文献[ 11]针对复杂多样的商业QoS建模需求,设计了支持数值型、不确定型(区间型、模糊型)数据的QoS模型,提出了基于模糊多属性决策理论的服务组合决策算法。
本文考虑到Web服务的QoS指标难以精确测量以及用户的QoS需求往往难以准确表达的问题,提出采用区间数形式对这些不确定信息进行建模,并在此基础上,引入用户满意度对组合服务进行综合评价,采用改进的粒子群算法寻找最优解,并通过实验验证了方法的可行性和有效性。
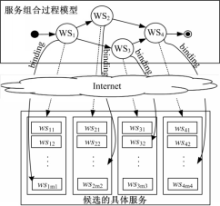
Web服务组合的过程从概念上可以分为四个阶段:定义、发现、选择和生成。定义阶段由业务专家对组合服务业务过程进行建模,业务过程模型中通常包含若干个任务节点(称为抽象服务);发现阶段按照组合服务中的各个任务的要求,查找和匹配合适的服务(称为具体服务),由于Internet上存在着大量功能相同或者近似的服务,因此对于同一个任务,往往可能发现多个服务,这些服务虽然在功能上是可替换的,但是通常具有不同的QoS水平,这些服务构成了每个抽象服务的候选服务集;选择阶段根据用户的QoS需求,为每个抽象服务从候选的服务集中选择合适的服务进行组合(如图1所示),该阶段是关系到整个Web服务组合是否能够成功的关键阶段,也是Web服务组合领域的一个研究重点;生成阶段的任务是在已选择的服务组件的基础上,自动生成带详细描述信息的服务组合方案。
对于包含n个抽象服务的组合服务CWS={WS1,WS2,…,WSn},每个抽象服务有一个由具体服务构成的候选服务集合WSi={wsi1,wsi2,…,wsim}。本文采用区间数形式定义服务的QoS指标,下面给出区间数的定义。
定义1 设R为实数域,称闭区间[x l,x u]为区间数,记作 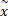
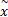
Web服务的QoS模型见定义2。
定义2 一个Web服务ws的QoS模型形式化地定义为
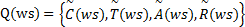
式中4个元素分别表示服务价格、执行时间、服务可用性和执行的可靠性,各指标的意义详见文献[ 11]。
定义2中,由于服务价格由服务提供者指定,通常是固定的,为了处理方便,本文将价格表示为上下界相等的特殊的区间数,而其他3项QoS指标的值在实际执行环境中是随机变化的,本文将这些随机变化的QoS指标表示为一个可动态自适应调整的区间。由于各QoS指标对应的随机变量所服从的分布未知,这里采用样本的性质对总体进行估计[ 4],对服务ws的最近n次执行所得的某项QoS指标值的样本为:q1,q2,…,qn,利用矩估计得到其数学期望和方差分别如公式(1)和(2)所示。
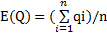 | (1) |
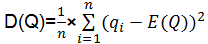 | (2) |
根据契比雪夫不等式,置信度为λ的某QoS指标的置信区间为, 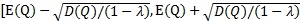
以上QoS指标中,服务可用性和执行的可靠性是效益型QoS指标,即指标值越高;质量越高,而服务价格和执行时间是成本型指标,即指标值越低,质量越高。
考虑到实际应用中用户的QoS需求难以准确表达的情况,本文将QoS需求也表示为区间数形式,定义如下。
定义3 用户对Web服务的QoS需求形式化地定义为
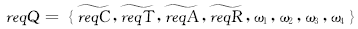
前4个元素依次代表用户对服务价格、执行时间、服务可用性和执行的可靠性的需求区间,后4个元素分别是以上各QoS指标的权重,代表了这些指标对用户的相对重要性,0≤ωi≤1, 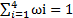
QoS感知的Web服务选择要求为每个任务节点选择一个合适的服务,形成一个可执行的组合服务能够在满足用户最低QoS需求的前提下,尽可能达到用户提出的QoS需求目标。
组合业务过程一般包括顺序、分支、并行、循环等4种结构,一个组合服务实例的全局QoS可以由单个服务的QoS计算得到,在不同流程结构下的QoS指标的聚合方法如表1所示。
| 表1 不同流程结构下的QoS指标的聚合函数 Table 1 Aggregation functions of QoS attribute on different workflow constructs |
在表1的分支结构中,pi表示第i个服务组件执行概率,并且 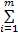
大部分服务选择方法没有充分考虑服务请求者的需求,以“ QoS值最大化”作为服务选择的原则,认为 QoS值越大的服务越优秀,越应该被选择,这种服务选择策略会使大量需求集中在少数几个服务上,导致这些服务的性能下降,从而降低组合成功率。事实上,根据边际效用递减规律,超出用户需要的质量对于提升其满意度没有显著影响, QoS达到一定的标准即可满足用户的需要[ 14]。本文引入用户满意度对组合服务方案进行评价,如果组合服务的 QoS未满足用户的最低需求,则用户满意度为0,如果达到或超出需求目标,则满意度为1。满意度是一个介于0和1之间的实数。下面给出对组合服务方案 cws的各 QoS指标的用户满意度计算方法。
服务价格的用户满意度 SD1计算如下:
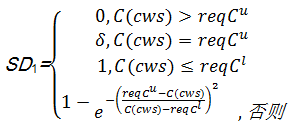 | (3) |
SD1的定义表明,组合服务cws的价格越接近用户价格需求区间的下界,则用户对价格越满意;若低于下界,则满意度为1;若高于上界,则满意度为0。
执行时间用户满意度 SD2计算如下
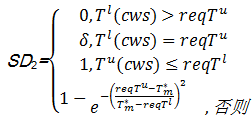 | (4) |
其中,[req 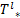
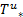
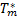
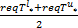
服务可用性用户满意度 SD3计算如下:
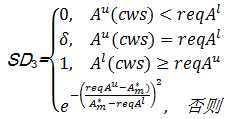 | (5) |
其中,[req 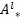
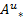
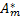
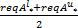
服务可靠性用户满意度 SD4计算如下:
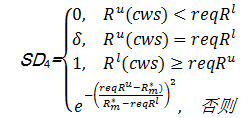 | (6) |
式中:[req 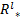
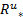
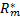
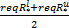
在上述定义中, δ是一个远小于1的纯小数。
根据公式(3) ~(6),得到组合服务用户满意度的综合评价为
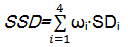 | (7) |
式中:ωi为权重,具体含义见定义3;SSD反映了用户对组合服务方案的总体满意度,其值越高,表明用户越满意。
本文方法的目标是在满足用户最低QoS需求的前提下,使用户满意度达到最高。数学描述如下:
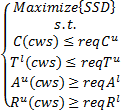 | (8) |
最优组合服务方案选择是一个NP难问题[ 2],而群体智能算法是解决这类问题的一个有效方法,粒子群优化算法(Particle swarm optimization,PSO)便是近年来得到较快发展的一种群体智能算法。
2.3.1 基本粒子群算法
PSO算法是由Kennedy和Eberhart于1995年提出的一种智能优化算法[ 15]。PSO算法中,每个粒子都被随机地分配一个位置和速度,根据个体经验和群体经验,在优化问题空间内自由飞行,逐渐接近最优解。PSO算法中,每个粒子代表了优化问题的一个潜在解,粒子通过自己飞行获得的个体认知以及与群体交流获得的社会认知来不断调整自身的位置,逐渐向最优解靠近。粒子i调整自身的飞行速度和位置的迭代方程如下:
vt+1=ωvt+c1r1(pt-xt)+c1r2(gt-xt) (9)
xt+1=xt+vt+1 (10)
式中:t是当前进化代数;xt和vt分别是粒子i在t时刻的位置和速度;pt是粒子i所经过的最优位置,即个体极值,代表个体认知;gt是群体发现的全局极值,代表社会认知;ω是惯性系数,主要作用是产生扰动,防止算法早熟收敛;c1和c2是加速系数(也称为学习因子),用于调节向个体极值和全局极值方向飞行的最大步长;r1和r2是均匀分布在[0,1]之间的随机数。
PSO算法具有参数少、收敛速度快的特点,在很多优化问题上表现出良好的搜索能力[ 16, 17, 18, 19]。但是,一方面由于Web服务选择问题属于离散空间问题,应用时需要重新定义算法的参数和运算;另一方面,PSO算法在快速收敛的同时也容易导致粒子过早聚集,陷入局部最优,从而出现早熟收敛问题。这些都限制了PSO算法在服务选择问题上的应用。针对这些问题,本文设计了一种改进的粒子群算法,即DBPSO算法,通过跟踪粒子位置的分布不断调整搜索空间边界,引导粒子在更有效的区域内进行搜索,从而减轻早熟收敛,提高收敛精度。
2.3.2 粒子的运动方程、运算规则以及适应值函数设计
首先,为问题域定义与PSO算法相关的数学对象及其运算规则,设组合服务CWS由M个抽象服务组成,每个抽象服务上有Ni(1≤i≤M)个候选服务,则针对服务选择问题有如下一些定义。
定义4 粒子的位置。粒子的位置 X是一个 M维向量, M是组合业务流程中抽象节点的数量,每个任务节点上的候选服务从0开始编号。则 X表示为 X =( x1,…, x i,…, x M),其中1≤ i≤ M,0≤ x i≤ N i -1, x i为整数。
定义5 粒子的速度。粒子速度 V实质是位移,用以改变粒子的位置,与粒子位置的定义类似,速度 V也是一个 M维向量,表示为 V =( v1,…, v i,…, v M),其中1≤ i≤ M,0≤ v i≤ N i -1。
定义6 位置的减法。位置 X2和 X1相减的结果是一个速度 V,表示为 V = X2 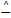
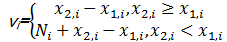 | (11) |
这里的“ -”和“ +”是一般意义的减法和加法,此定义保证了运算结果仍然是区间[0,Ni -1]内的整数。
定义7 位置与速度的加法。位置与速度的加法实现了粒子位置的移动,表示为 X = X 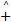
x i =x i +v i mod N i (12)
定义保证了位置的变化量控制在区间[0,Ni -1]内。
定义8 速度的数乘。速度的数乘表示为 V2 =c 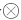
v2, i =round( c· v1, i) mod N i (13)
这里的“·”是一般意义的乘法, round表示就近取整,定义保证了运算结果是[0,Ni -1]内的整数。
定义9 速度的加法。两个速度的加法得到一个新的速度,表示为 V =V1 
v i =( v1, i +v2, i) mod N i (14)
定义保证了运算结果仍然是[0,Ni -1]内的整数。
根据以上定义,服务选择问题的离散粒子群算法的运动方程可以描述为
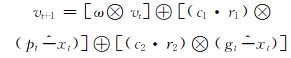 | (15) |
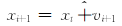
根据公式(7)和公式(8)定义适应值函数为f= 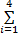
2.3.3 动态边界策略
PSO算法进化的后期,易出现停滞现象,即粒子聚集并且移动速度接近于0,难以逃离局部极值区域,从而导致早熟问题。在大多数情况下最优解并不处于粒子聚集的位置,而是隐藏在聚集区域附近的某个地方,因此粒子的运动可以为发现最优解提供有效指引,基于这一考虑,本文提出采用DBPSO算法寻找最佳组合方案,在进化过程中,该算法通过动态调整搜索空间边界对粒子飞行位置进行跟踪,当发现粒子聚集时,对边界进行一定的扩展,并在新的搜索空间内激活停滞粒子,使粒子逃离局部区域,去寻找最优解。
分别通过公式(17)~(19)对搜索空间的左边界进行收缩、扩展及重置,分别通过式(20)~(22)对搜索空间的右边界进行收缩、扩展及重置。
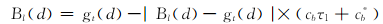 | (17) |
Bl(d)=gt(d)-|Bl(d)-gt(d)|×(obτ2+1) (18)
Bl(d)=gt(d)-|Bl(d)-X min |×τ3(19)
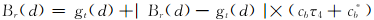 | (20) |
Br(d)=gt(d)+|Br(d)-gt(d)|×(obτ5+1) (21)
Br(d)=gt(d)+|X max -Br( d) |×τ6(22)
以上公式中: d是当前维; gt( d)是全局极值点; cb是收缩率; 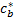
公式(17)~(22)表明,边界的调整均以全局极值点为核心在一定范围内进行随机收缩或者扩展。如果当前边界在第d维被重置,表明粒子在第d维聚集在一起,此时为了提高粒子的多样性,算法随机挑选少量粒子激活,促使其逃离局部极值区域。
2.3.4 算法步骤
DBPSO算法在标准PSO算法的每一次迭代结束后,执行以下3个步骤。
(1)标记当前边界。在第d维,检查是否有一些粒子飞出了当前边界[Bl(d),Br(d)],如果有粒子飞出,则在第d维将边界标志置为true,否则置为false。搜索空间首先被初始化为问题空间。
(2)动态调整搜索空间。在这一步骤中,分别处理搜索空间每一维的左右边界。当边界与全局极值点的距离大于阈值ε时,若该维上的边界标志为false,则利用公式(17)和公式(20)收缩边界,否则利用公式(18)和公式(21)扩展边界;当边界与全局极值点的距离等于或者小于阈值ε时,表明发生粒子聚集,则利用公式(19)和公式(22)进行边界重置。
(3)激活处于停滞状态的粒子,清除其个体经验。若当前边界在第d维被重置,则在当前边界内为速度加上一个服从正态分布的随机数,以激活粒子,这一步骤是为了提高种群的多样性,同时,由于粒子很容易受到其个体经验的影响而不能从所发现的极值中逃离,因此需要清除它们的个体经验,具体做法是将粒子的个体极值设置为其当前位置。
当达到最大迭代次数时则算法终止。
实验分为两个部分。第一部分,比较采用本文的自适应区间型QoS模型与采用确定值型QoS模型对Web服务组合成功率的影响,服务组合成功率指组合服务计划成功运行的数量占服务请求数量的百分比。第二部分,比较采用与未采用动态边界策略的PSO算法(称为SPSO算法)的性能。实验在含有6个任务节点的组合服务流程上进行,实验运行环境为Intel Pentium双核(2.2GHz)处理器,2 G内存,采用Matlab7.4.0编写仿真程序。
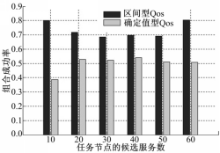
首先,通过实验对基于自适应区间型与确定值型QoS模型的服务组合的成功率进行比较,其中,确定值型的QoS取历史日志的期望。实验为每个任务节点随机生成10~60个候选服务,各候选服务的执行时间、可用性和执行的可靠性参数在给定的范围内随机波动。实验中,置信度λ取0.05,公式(3)~(6)中的δ取0.01,各QoS指标的权重均取0.25。对每个任务节点的候选服务数从10递增到60的情况分别进行了实验,每种情况下的组合成功率取运行100次的平均值,实验结果如图2所示。
从图2可见,对于不同规模的候选服务,基于自适应区间型QoS模型的组合成功率明显高于确定值型的。这是由于本文的QoS指标度量采用了自适应、动态调整的策略,使QoS接近真实情况,区间的采用也使得服务选择可以基于模糊的方式进行,从而在一定程度上提高了组合成功率。
第二部分实验旨在比较DBPSO和SPSO的性能。为便于比较,本部分实验首先采用穷举法找到全局极值f g_best,此外,为保证算法比较的客观性,实验让各算法从问题空间相同的位置出发寻找最优解。这里使用算法综合性能指标(Algorithm comprehensive performance index,ACPI)衡量算法的性能,ACPI的计算式如下:
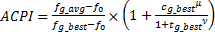 | (23) |
式中:f g_avg是算法重复执行n次的平均适应值,f0是整个迭代过程中的最劣值,即迭代开始时全局最优值;(f g_avg-f0)/(f g_best-f0)用于衡量所得解的质量,该值越大表明所得的解越接近全局极值,算法的寻优能力越强;c g_best是算法重复执行n次发现极值所用的总次数;t g_best是算法重复执行n次发现极值所用的总迭代代数;u和v分别是c g_best与t g_best重要程度的影响因子,显然,算法发现最优解的次数越多,所用的迭代代数越少,则算法越优。
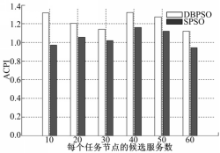
实验中,两种比较算法除了与动态边界策略相关的参数外,其他参数均取相同的值,采用的主要参数取值为:cb=0.03,ob=0.1,ε=1×10-5,u=2.0,v=1.0,其中,cb,ob和ε的取值是通过在本实验开始前进行的参数取值实验中获得的最佳参数集中取得;u和v的取值表明实验更加关注算法的寻优能力;其他参数参见文献[ 20]。实验中,种群规模为20,好邻居个数为3,最大进化代数为500。各算法的ACPI取实验运行150次的平均值,实验结果如图3所示。
从图3可见,在不同规模的解空间中,DBPSO总是能够获得比SPSO高的综合性能,平均ACPI较SPSO高14.44%。
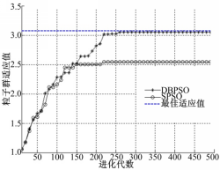
图4所示为在每个任务节点有40个候选服务的情况下,粒子群适应值的进化收敛曲线。虽然DBPSO收敛代数略高于SPSO,但是相比于SPSO,DBPSO能够获得较高的收敛精度。
提出了一种支持不确定信息的Web服务选择方法。该方法对Web服务的QoS模型进行了扩展,支持区间型不确定QoS指标的定义,采用自适应、动态调整策略对QoS指标区间进行度量;考虑到人类思维的模糊性,用户QoS需求也建模为区间数形式;在此基础上,提出基于用户满意度的组合方案评价方法;在PSO算法中引入动态边界调整策略,采取改进的粒子群算法寻找最优组合方案。仿真实验从组合成功率和服务选择算法综合性能两个方面验证了本文所提方法的有效性和可行性。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|