盛刚(1978),男,博士研究生.研究方向:云计算安全.E-mail:shenggang@neusoft.edu.cn
为解决云计算环境下偏好top-
The problem of correctness of authenticating results of preference top-
在云计算环境中,数据所有者将数据管理任务委托给云服务提供商。云服务提供商端的数据可能会遭到攻击或者不忠实地执行查询,从而返回给客户不正确的结果,因此,在向客户返回查询结果的同时还要返回验证对象以检验查询结果的正确性。
本文提出了云计算中偏好top- k查询结果的正确性验证问题。查询结果的正确性包括两方面:①查询结果完全来自数据所有者,没有被篡改、不是伪造的;②查询结果中的数据没有遗漏。
偏好top- k查询根据客户指定的评分规则计算得分最高的前 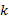
在偏好top- k查询的研究成果中,DG的效率较高并且呈现为规则的数据结构。作者以DG为基础提出了基于哈希的验证支配图(Authenticated dominant graph with Hash,ADG-H)和基于数字签名的验证支配图(Authenticated dominant graph with signature,ADG-S)。ADG-H能有效地验证一次性偏好top- k查询结果的正确性,但对于连续监控,在更新频繁和连续监控数量大的情况下会引起大量的网络传输。而ADG-S,只有当数据更新影响到连续监控结果或验证对象时才与客户进行必要的网络传输,大大减少了网络传输量。
Zou Lei等[ 4]提出了支配图(Dominant graph,DG)的概念,根据数据间的支配关系构建支配图。与其他偏好top- k查询方法相比,支配图具有查询空间小、查询速度快的特点[ 4]。
Hacigumus等[ 5]在ICDE 2002提出数据库服务模型,可以认为是云计算框架的一个组成部分。Merkle R首次提出了MH-Tree[ 6],后来被用在对外包数据库中的查询结果进行正确性验证[ 7]。查询结果正确性验证研究领域中有众多研究成果[ 8, 9, 10, 11, 12, 13],与本文最相关的是最邻近查询结果的验证。文献[12]提出了MR-Tree用以验证最邻近查询结果的正确性,文献[13]提出AMN和C-AMN对多步最邻近查询结果进行验证。但最邻近查询与偏好top- k查询在实现原理上有很大的不同,因此不能使用最邻近查询的验证方法对偏好top- k查询进行验证。
在连续监控结果验证的研究领域中,文献[ 14]提出了REF和CADS对外包数据库普通查询的连续监控结果进行正确性验证,有数据更新发生时向用户发送新的验证对象,以确保用户的结果是最新的。该文献基于普通关系数据库,其内在机制与偏好top- k查询及支配图截然不同,提出的方法亦不适用于偏好top- k查询的正确性验证。
相关符号及其含义为: D表示整个数据集; N表示支配图中的节点; RS表示top- k查询的结果集; R表示查询结果集中的一个结果; VO表示验证对象; P( N)表示节点 N的父节点集合; C( N)表示节点 N的子节点集合。
接下来给出几个定义,设 N1、 N2、 N3为3个数据(在不引起混淆的情况下,也称数据为节点),每个数据都有相同数目的若干个分量。
定义1 支配[ 4]:两个节点 N1和 N2如果 N1的每个分量都大于等于 N2相应的分量,并且至少有一个分量大 N2相应的分量,则称 N1支配 N2。
定义2 支配图[ 4]:按照数据间的支配关系,将互不支配的数据放在一层,将被支配的数据放在下一层,这样构建的结构称为支配图。
定义3 父节点:如果 N1支配 N2,则在支配图中, N1为 N2的父节点。
定义4 子节点:如果 N1支配 N2,则在支配图中, N2为 N1的子节点。
定义5 兄弟节点:如果 N1支配 N2和 N3则在支配图中, N2和 N3为兄弟节点。
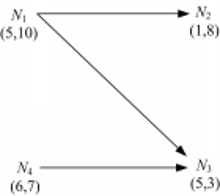
例如,设 N1=(5,10), N2=(1,8), N3=(5,3), N4=(6,7),构建的支配图如图1所示。
在图1中, N1支配 N2和 N3, N1为 N2和 N3的父节点, N2和 N3为 N1的子节点, N2和 N3互不支配、互为兄弟节点; N1和 N4互不支配、互为兄弟节点, N4支配 N3, N4为 N3的父节点, N3为 N4的子节点。
为对云计算中偏好top- k的查询结果进行正确性验证,在支配图的基础上提出了ADG-H。
构建ADG-H时,需要在DG构建过程的基础上计算节点哈希值,对根节点进行数字签名并为以后验证对象的提取工作做准备,步骤如下:
(1)运用DG构建算法构建ADG-H。与DG不同的是,ADG-H为每个节点增加一个哈希值项。
(2)增加根节点层。ADG-H的顶层现为Layer 1,为方便以后验证对象的提取,在Layer 1前增加一层Layer 0,并为该层增加一个节点 Nroot作为整个ADG-H的根节点,Layer 1中所有节点皆为其子节点,该节点各分量的值置为整数或浮点数中的最大值。 Nroot及其值为参与运算的各方所共享。
(3)计算哈希值。从ADG-H的最后一层依次向前直至Layer 0,为每层中的每个节点计算哈希值,如果某节点没有子节点,则该节点的哈希值为其值的哈希;如果有子节点,则该节点的哈希值为其值与其所有子节点的哈希值的连接的哈希,连接时按照子节点的序号从小到大排列。
(4)数字签名。对 Nroot的哈希值(记为 hroot)进行数字签名,得到 sig(h root )。
在ADG-H中,当插入、删除、修改等数据更新发生时需要进行数据更新和哈希更新。数据更新按照DG更新算法进行;随后进行哈希更新,重新计算在数据更新阶段受影响的各节点的哈希值。
以插入为例,首先进行数据更新。设要插入的数据为 N1,首先按照DG的插入算法执行插入:经过搜索, N1应该插入到Layer d中,将Layer d中受 N1支配的节点插入到Layer d+1中,对Layer d+1及以后的各层做相同处理,设最终受影响的层为Layer u。简要插入算法见算法1,详见文献[ 4]。
算法1 Insert Algorithm.
输入:DG;要插入的节点NI;
输出:NI所在层d;插入到最后一层的节点集合S;最终影响的层编号u;
①初始化:建立两个空集合S和T;
②经过搜索,NI应该插入到Layer d中;S={NI};m=d;
③将集合S中每个节点的子节点放到T中;
④将T中的每个节点从Layer m中删除;
⑤将S中的节点插入Layer m中,重新计算Layer m-1和Layer m两层节点间父子关系;
⑥如果T为空,插入过程结束,转⑦;否则,清空S,将T中节点放到S中,m加1,如果m值大于当前DG最后一层的编号,新建一层Layer m,转至③;
⑦插入过程结束,u=m,返回S、d和u。
数据插入完成后进行哈希更新,见算法2。首先计算插入到Layer u中的节点的哈希值,然后计算这些节点的父节点的哈希值,依次向前逐层更新各层中受影响的节点的父节点的哈希值,直至最后到达根节点 Nroot,更新 Nroot的哈希值。
算法2的时间复杂度在最坏时为 O(| D|),即将ADG-H中每个节点的哈希值重新计算一次,其中 D表示数据集的规模。
算法2 UpdateHash Algorithm.
输入:DG;节点集合S;
输出:根节点的数字签名sig(hroot);哈希值更新过的节点集合U;
①初始化:建立空集合T,U;
②重新计算S中每个节点的哈希值;U=U∪S;
③将S中每个节点的所有父节点放到T中;
④清空S,将T中所有节点放到S中,清空T;
⑤如果S不为空,转至②;
⑥重新计算根节点的数字签名sig(hroot);
⑦哈希值更新过程结束,返回sig(hroot)和U。
ADG-H中的删除和修改与插入的过程类似,首先执行DG中的删除和修改算法,将最后一层中受影响的节点返回,然后执行算法2,更新相关节点的哈希值并重新计算根节点的数字签名。
收到客户端查询请求后,服务提供商端执行查询算法得到查询结果 RS。但是由于服务提供商端可能会遭到攻击,数据可能会被篡改,服务器也可能由于某种原因而没有忠实地执行查询,导致客户端可能收到不正确的查询结果。这就需要服务提供商根据 RS从ADG-H中提取验证对象 VO,以供客户用来对 RS的正确性进行验证。
设 RS为{ Nroot, R1, R2,…, Rk},为了表达顺畅, RS中的 N root也记为 R0,即 RS表示为{ R0, R1, R2 ,…, Rk },从 R0到 Rk按照得分从高到低排序。在MH-Tree和MR-Tree的查询结果中一定存在叶子节点,而验证支配图的查询结果中则可能不存在叶子节点,因此,ADG-H中验证对象的提取与MH-Tree和MR-Tree相比更为复杂一些。
从验证支配图中提取的验证对象只要能够同时满足真实性和有效性,即可以实现对 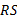
真实性:对于 Rm∈ RS, m为整数,且0≤ m≤ k, R m为真实的、来自数据所有者,没有被篡改、不是伪造的。
有效性:对于 R0∈ RS, R0为整个支配图中得分最高的点;对于 Rm+1∈ RS, m为整数,且0≤ m≤ k, R m +1为整个支配图中 R m后得分最高的点。
为满足真实性和有效性要求,经过对验证对象的提取过程进行观察和分析,给出定理1用以指导验证对象的提取。
定理1 对于偏好top- k查询结果 RS中的每个节点 R,将 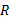
证明(真实性) 在验证时,结合 VO从 RS中处于最后一层的节点开始逐层计算各层节点的哈希值,用最终得到的 R0的哈希值对数字签名进行验证。如果验证通过,表明返回的 RS和 VO中所有节点的值为正确的;否则表明 RS或 VO中存在不正确的节点。证毕。
证明(有效性) 当 m=0时,考虑 R0。节点 R0即 N root的值为参与计算的各方所共知,且 R0的值是整个支配图中最大的,显而易见,对所有查询 R0都必然在 RS中。
当 m=1时,考虑 R1。由于Layer 0中只有一个节点 R0,则 R1必然在Layer 1中,且为 R0的子节点。由于已经将 R0的所有子节点放到 VO中,可以计算出 R0的每个子节点的得分,能够表明 R1为 R0后整个支配图中得分最高的点。
当 m=2时,考虑 R2。可以区分为两种情况:① R2为 R0的子节点;② R2为 R1的子节点。根据支配图的原理,如果某节点在 RS中,则该节点至少有一个父节点在 RS中[ 4]。而在 RS中, R2前只有 R0和 R1, R2要么为 R0的子节点,要么为 R1的子节点,不存在第三种情况。因此,不论 R2为 R0或 R1的子节点,在处理 R0和 R1时已经将 R0和 R1的所有子节点放到 VO中,所以能够表明 R2为 R1后整个支配图中得分最高的点。
当2< m≤ k时,对于 Rm。 Rm必然为{ Ri |0≤i≤ m-1}中某节点的子节点,此 m个节点的子节点都已经放到 VO中,所以能够表明 Rm为 Rm-1后整个支配图中得分最高的点。证毕。
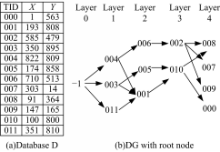
重画的文献[ 4]中的图1如图2所示,其中图2(a)为数据集,图2(b)为增加了根节点 N root的DG,根节点编号为-1,所在层为Layer 0。
用函数 F=0.6* X+0.4* Y进行top-2查询, RS为{-1,4,6}, VO为{-1(3,4,11),4(1,6),6(2)}。
用函数 F=0.5* X+0.5* Y进行top-4查询, RS为{-1,4,3,6,11}, VO为{-1(3,4,11),4(1,6),3(1,5),6(2),11(1)}。
一次性查询是指客户向服务提供商提交查询后,服务提供商立即执行查询并将查询结果和验证对象返回给客户,查询结束。连续监控是指客户向服务提供商注册查询后,服务提供商首先执行查询,并将查询结果和验证对象返回给客户,再对以后的数据更新进行监控,如果数据更新影响到查询结果或验证对象,将受影响的查询结果和验证对象返回给客户,直至客户注销该连续监控为止。
根据算法2,每次数据更新之后ADG-H根节点的数字签名都会随之更新。不论数据更新是否影响到监控查询的结果,至少需要发起一次网络传输将最新的根节点的数字签名发送给客户。如果有较多的连续监控和较频繁的数据更新,会引起大量的网络传输,也加大了服务器端的负担。
为减少网络传输量,作者提出了ADG-S。以DG为基础,ADG-S为各节点增加数字签名。
ADG-S的构建过程与ADG-H类似,不同的是:①ADG-S的每个节点中存放的是数字签名;②对没有子节点的节点直接对其值进行数字签名,对有子节点的节点则对节点的值和其子节点的值的连接进行数字签名。
在ADG-S中,当插入、删除、修改等数据更新发生时,同样需要进行两种类型更新:数据更新和数字签名更新。数据更新按照DG的更新算法执行;数字签名更新重新计算数据更新阶段受影响的节点的数字签名。
以插入为例。首先更新数据。设插入数据为 NI执行算法1后,得到 NI 所在层的编号 d、最终影响到的层编号 u和插入到最后一层的节点集合 S。然后更新数字签名,重新计算在插入过程中受影响的节点的数字签名,见算法3。先计算插入到Layer u中的节点的数字签名,然后计算这些节点的父节点的数字签名,逐层计算各层中受影响的节点的父节点的数字签名,直至最后到达Layer d-1,更新 NI的父节点数字签名,数字签名更新结束。算法3的时间复杂度在最坏情况下为O(|D|),即将验证图中每个节点的数字签名重新计算一次。
算法3 UpdateSignature Algorithm.
输入:Insert算法的返回值 S和d
输出:新计算过数字签名的节点集合 P
①初始化:建立两个空集合P和T,设变量m为S中节点所在层的编号;
②重新计算S中每个节点的数字签名,P=P∪S;
③将S中每个节点的所有父节点放到T中;
④清空S,将T中节点放到S中;
⑤如果m等于d-1,数字签名更新结束,转⑥;否则m减1,转②;
⑥返回集合P。
计算节点 N的数字签名时,如果 N已有数字签名,需将现有的数字签名作为 N值的一部分参与计算。这样,如果多次更新影响到某连续监控的结果或验证对象,但服务器端没有将某次更新发送给用户,客户会检测到。
ADG-S中的删除和修改与插入类似,首先执行删除和修改算法,然后执行算法3,重新计算删除和修改过程中受影响的相关节点的数字签名。
定理1对使用ADG-S时验证对象的提取依然适用。用户注册连续监控后,服务提供商执行查询算法,并提取验证对象,保存查询结果和验证对象,并将查询结果和验证对象发送到Client。在以后的数据更新过程中,如果某次更新影响到某监控的结果或验证对象,则将受影响的节点信息发送到相应的Client,否则不发送任何信息。与ADG-H相比,ADG-S只有在必要时才发送信息,大大减少了不必要的网络传输。
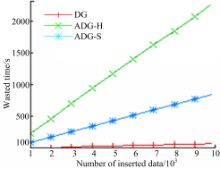
试验环境为Intel Core2 1.6 GHz,2 GB内存的PC机,用Java语言实现了所用的数据结构和算法,实验中随机生成了呈均匀分布的数据集。实验以DG为基准,比较ADG-H和ADG-S在构建和更新两方面的性能。比较ADG-H和ADG-S在连续监控方面的性能。由于DG、ADG-H和ADG-S具有相同的搜索空间,ADG-H和ADG-S具有相同的查询时间和验证对象大小,不再进行比较。
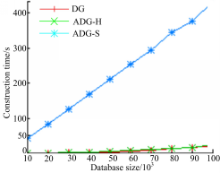
构建实验以DG的构建时间为基准,结果如图3所示。由于MD5的效率较高,选用MD5作为哈希函数构建ADG-H,所用时间略多于DG,只有数据量很大时构建ADG-H所用时间才明显多于DG。构建ADG-S时选用RSA作为数字签名方案,由于RSA数字签名方案代价较高,所用时间明显比DG和ADG-H都多。
更新实验同样以DG的更新数据为基准,图4为插入所用时间,图5为删除所用时间。可以看出,ADG-H的更新时间比DG多,ADG-S的更新时间最多。
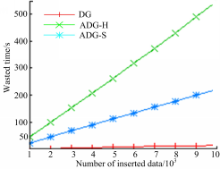
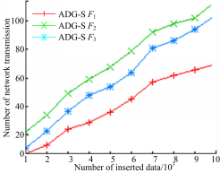
图6为不同查询比较,设 k=200, F1=(0.3,0.7), F2=(0.9,0.1), F3=(0.5,0.5)。可以看出,ADG-H中,每一次更新都会影响连续监控的验证对象,从而引起一次网络传输;ADG-S中,只有当本次更新影响到连续监控的结果或验证对象时,才进行一次网络传输,网络传输量明显比ADG-H少得多。图7为不同 k,对 k分别取100、200、500,设 F=(0.5,0.5),可以看出 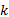
在支配图的基础上提出了ADG-H和ADG-S两种验证图以解决云计算环境下偏好top- k查询结果的正确性验证问题。ADG-H能够有效地验证一次性top- k查询结果的正确性。ADG-S能够有效地验证连续监控结果的正确性。与ADG-H相比,ADG-S只有当数据更新影响到连续监控的结果或验证对象时才发起网络传输,向用户发送最新结果,大大减少了网络传输量,同时也降低了服务提供商端客户端的负担。我们未来将继续研究如何提高ADG-S的更新效率,并对云计算环境下偏好top- k查询的隐私保护进行研究。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|