刘玉(1989),男,博士研究生.研究方向:汽车车身结构设计理论与轻量化技术. E-mail:lyu11@mails.jlu.edu.cn
针对客车侧翻事故中侧窗立柱承受侧翻碰撞力矩不相等的特点,提出了变截面冲压立柱的解决方案,对冲压立柱的截面尺寸进行了设计。先用有限元方法对等截面立柱车身段进行了仿真分析,并通过实验验证了该方法的有效性。然后运用该有限元法对变截面立柱客车车身段进行仿真分析,结果表明:变截面冲压立柱能大幅度提高整车的侧翻安全性。
According to the characteristic that, in bus rollover accident, the window pillar withstands unequal rollover crash moments, an approach of variable cross-section stamping column is proposed and cross-section dimension of column is studied. First, finite element method is used to simulate the performance of uniform cross-section stamping column, and experiments is conducted to validate finite element method. Then, finite element method is applied to simulate the performance of variable cross-section stamping column in bus rollover. Results show, compared with uniform cross-section column, the variable cross-section stamping column can significantly improve the safety in bus rollover accident.
客车侧翻事故易造成群伤群死现象,是最严重的交通事故之一[ 1, 2]。在客车侧翻过程中,主要承受冲击载荷、吸收碰撞能量的是车身骨架的封闭环结构[ 3],其中又以侧窗立柱为主要的变形吸能部件,因此侧窗立柱的结构设计直接影响到封闭环的抗侧翻特性,进而影响到客车整车的侧翻安全性能[ 4]。客车侧翻时,侧窗立柱顶部首先与地面接触,导致其所承受的碰撞力矩沿立柱长度方向由上向下逐渐增大[ 5]。从理论设计角度分析,为保证侧窗立柱变形均匀、减小车身结构的变形量,侧窗立柱截面尺寸由上至下应该逐渐增大。而传统客车侧窗立柱均采用等截面尺寸的矩形钢管[ 6],不能满足这一理论设计条件。基于上述分析,本文提出一种变截面冲压立柱的解决方案。
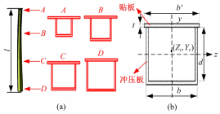
图1为现有的客车封闭环及侧窗立柱结构位置示意图。
变截面冲压立柱由两部分组成,一部分是经过冲压成型的“U”形冲压板,冲压工艺可以实现立柱截面尺寸按设计要求改变;另一部分是与冲压板焊接的贴板,贴板宽度保持不变,并且大于冲压板的最大宽度,贴板位于冲压板外侧,方便车窗玻璃粘接,如图2(a)所示,各截面尺寸不等。冲压立柱长度为 l,任取其中一个截面,如图2(b)所示。冲压板宽度为b,深度为d,贴板宽度为b',板厚为t。
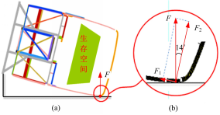
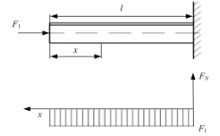
客车发生侧翻碰撞时,侧窗立柱受到垂直于地面的作用力 F,如图3(a)所示。将 F分解为沿侧窗立柱方向的轴向力 F1和垂直于侧窗立柱方向的横向力 F2如图3(b)所示。侧窗立柱与地面的夹角为14°,因此 F1/ F2= tan14°≈0.25。
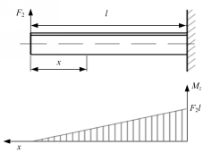
在横向载荷作用下,对侧窗立柱进行等强度设计,将侧窗立柱简化为一端固定的悬臂梁,另一端受到横向载荷 F2图4为悬臂梁模型示意图及其受到的弯矩示意图。
弯曲截面应力计算公式为
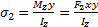 | (1) |
式中所采用的坐标系如图2(b)所示。由式(1)可知:侧窗立柱各截面弯曲应力值 σ2与该截面承受的弯矩 Mz成正比,与截面惯性矩 Iz成反比。为保证各截面弯曲应力值相等,随着弯矩的增大,需要逐渐增大截面抗弯惯性矩 I z。首先计算冲压立柱截面的形心坐标值与惯性矩。
形心计算:如图2(b)所示,用( Z c ,Y c)表示冲压立柱截面的形心坐标。截面形状左右对称,所以 Z c由材料力学静矩理论可知,若某一轴通过截面图形的形心,则截面图形对该轴的静矩等于零,即 S z=0, S y=0。
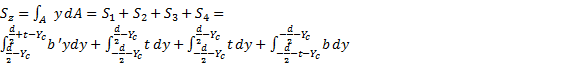 | (2) |
式(2)为图形对 Z轴的静矩计算公式,令 S z=0,可求得:
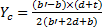 | (3) |
即截面形心坐标为 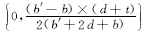
惯性矩计算:侧窗立柱在横向载荷 F2 作用下,主要产生绕 Z轴的弯曲变形,计算冲压立柱截面相对于Z轴的惯性矩为
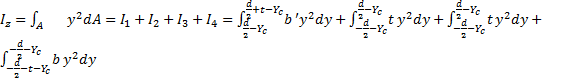 | (4) |
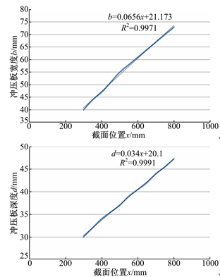
将截面形心坐标( Z c ,Y c)、惯性矩 I z代入式(1)中,令截面应力值 σ2等于一个定值,求解各截面尺寸与截面位置之间的变化关系。为节约运算时间、提高运算效率,本文编写Fortran程序进行计算,结果如图5所示。
图6为冲压立柱悬臂梁模型受到轴向载荷 F1作用的示意图及其承受的轴向力示意图。
轴向应力计算公式为
 | (5) |
由式(5)可知:立柱各截面轴向应力值 σ1与其所承受的轴向力 F1成正比,与截面面积 A成反比。从图6可以看出立柱各截面承受的作用力相等,为保证立柱各截面轴向应力值相等,立柱各截面尺寸应该相等。
侧窗立柱顶部与顶盖相连接,此接头区域受力情况较为复杂,因此在侧窗立柱等强度设计时避开顶部接头区域,选择设计区间为200~1000 mm(立柱全长 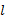
| 表1 侧窗立柱截面尺寸设计 Table 1 Section size design of side window pillar |

式中: b x 、 d x 分别为冲压立柱 x截面冲压板的宽度、深度值。
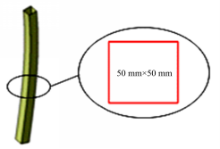
本文通过仿真对比考察变截面冲压立柱对客车侧翻安全性的影响,选取用于对比的客车车身段侧窗立柱如图7所示,其各截面尺寸相同,均为50 mm×50 mm,壁厚为3 mm。
变截面冲压立柱质量计算表达式为
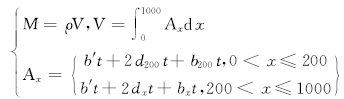 | (6) |
令 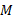
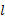
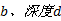
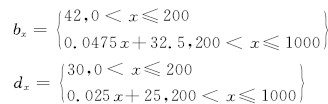
前文在对侧窗立柱进行强度设计时,对其受力情况做了一定的简化,为了更加全面地考察变截面冲压立柱对客车侧翻安全性的影响,本文将采用有限元仿真方法进行对比分析。
建立等截面立柱客车车身段模型,并对其进行有限元仿真分析。图8为等截面立柱车身段模型侧翻仿真最大变形图。为了验证有限元仿真分析的可靠性与有效性,本文对该等截面立柱车身段进行了真实侧翻实验,并在车身段乘员生存空间的外边界上选取16个实验点,如图9所示。将实验过程中变形钢针的剩余量,即生存空间实验点到侧窗立柱的最近距离作为验证指标,表2为实验与仿真结果数据。
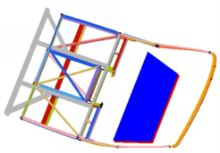 | 图8 等截面车身段侧翻仿真最大变形图Fig.8 Maximum deformation of uniform cross-section body segment rollover simulation |
 | 图9 等截面车身段侧翻实验结果及测量点Fig.9 Results and measurement point of uniform cross-section body segment rollover test |
| 表2 实验与仿真结果数据 Table 2 Data of test and simulation |
对比实验与仿真结果数据可知,仿真中生存空间前端相对后端变形稍小的趋势与实验一致。仿真结果与实验数据较为接近。由于实验过程中变形钢针脱落,导致前段测点3、后段测点8的实验数据无法记录。对其余14个实验点进行统计,得到平均误差值为6.14%。由此可以验证客车车身段有限元仿真的可靠性和有效性。
本文在前文已经经过实验验证的等截面立柱客车车身段模型的基础上,将等截面立柱替换为变截面冲压立柱,其余结构仍采用等截面立柱车身段模型结构,仿真计算条件保持不变,并进行有限元仿真分析。图10为变截面冲压立柱车身段侧翻仿真最大变形结果示意图。在变截面冲压立柱车身段模型中选取与等截面立柱车身段相同的16个实验点,统计其到侧窗立柱的最近距离作为对比指标,与等截面立柱车身段仿真结果进行对比,得到表3中的数据。
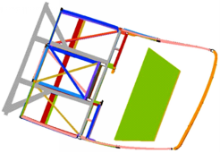 | 图10 变截面车身段侧翻仿真最大变形图Fig.10 Maximum deformation diagram of variable cross-section body segment rollover simulation |
由表3数据可知:变截面冲压立柱车身段侧翻仿真中16个实验点生存空间到侧窗立柱的最近距离均大于等截面立柱车身段,距离值平均提高了48.8%,可见变截面冲压立柱车身段的结构变形量明显小于等截面立柱车身段,即变截面冲压立柱车身段侧翻安全性能明显优于等截面立柱车身段。由于车身段中封闭环的抗侧翻性能可以直接反映整车的侧翻安全性能,因此变截面冲压立柱方案对客车整车的侧翻安全性能有很大的改善作用。
| 表3 侧翻仿真结果对比 Table 3 Results contrast of rollover simulation |
根据客车侧翻时侧窗立柱承受碰撞力矩不相等的特点,提出了变截面冲压立柱的解决方案,重点研究了变截面冲压立柱的截面尺寸,通过实验验证和仿真对比分析得出结论:变截面冲压立柱对整车的侧翻安全性有很大的改善作用。本文在保证变截面冲压立柱与等截面侧窗立柱质量相同的前提下,得出上述结论;如果保证客车的侧翻安全性能相同,则可以通过变截面冲压立柱实现客车车身轻量化的设计目标。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|