祁冰(1980),男,副教授,博士.研究方向:图像噪声处理.E-mail:visual_myself@126.com
多传感器图像在采集、传输和转换中常常会受到成像设备和外部环境中脉冲噪声的干扰,受到该类型噪声污染的像素点通常表现为亮度与其邻域像素点对应的亮度值存在明显差异,视觉效果上也会出现一定程度的黑白亮暗点,这不仅大大降低了图像质量,也为图像分割、图像融合[ 1]等一系列后续工作带来很大不便。不仅如此,脉冲噪声的存在还会对图像识别带来很大干扰,极易引起决策系统的误判或漏判,因此如何有效地去除源图像中的脉冲噪声已成为图像预处理领域内的一个热点问题。
目前主要的图像去噪方法分为两类:一类是基于多尺度多分辨率变换的图像去噪方法,代表性算法有离散小波变换去噪法[ 2],轮廓波变换去噪法[ 3, 4]以及近几年兴起的非下采样轮廓波变换(Non-subsampled contourlet transform,NSCT)去噪法[ 5, 6],其中以NSCT去噪法效果最为理想,但这几种方法得出的最终去噪图像均包含有“划痕”状的虚假信息;而另一类则是基于人工神经网络的图像去噪算法,目前应用最为广泛,其中去噪效果较好的是脉冲耦合神经网络(Pulse coupled neural networks,PCNN)方法[ 7, 8, 9],但异常复杂的神经元框架结构以及大量待确定参数的存在却是其无法回避的问题。交叉视觉皮层模型(Intersecting cortical model,ICM)[ 10, 11]是一种崭新的具有重要生物学背景的大脑视觉皮层模型,同PCNN相比,它的待定参数较少,计算复杂度大幅降低,且具备优越的图像处理性能[ 12, 13],但将ICM用于图像去噪时,包括迭代次数、衰减系数以及幅度常数等繁杂的参数设置仍是制约其性能的瓶颈。
另一角度,国内外近年也出现了几种性能较为优越的脉冲噪声去除算法[ 14, 15, 16],如Kenny等[ 14]的自适应模糊中值滤波算法虽然具有较好的去噪效果,但在参数设置和运行时间上仍存在缺陷;Srinivasan等[ 15]提出将3×3窗口的像素进行排序,从而获得最小(大)值及中值,从而判断像素是否被污染及计算修正像素的灰度值;吕宗伟等[ 16]采用3×3窗口内的非噪声像素点的灰度均值作为噪声像素点的修正值,取得了较好的效果,且具有较短的运行时间,但上述两种算法均采用固定大小的区域窗口分析各像素点,而未能从图像的实际像素灰度值分布自适应调整去噪窗口的尺寸,灵活度较差,因此在图像去噪效果上仍有待提高。
作者通过对经典ICM的深入分析得出其模型框架中的不足,进而对其进行改进得到一种改进型ICM(IICM),然后利用IICM的赋时矩阵信息确定受脉冲噪声污染的像素点的具体位置,最后提出了基于IICM的自适应图像去噪算法,完成对噪声像素点的去噪处理。最后通过仿真实验将本文方法与近年出现的几种较为经典、性能较为优越的脉冲噪声处理方法进行了比较,结果表明本文去噪方法取得了良好的去噪效果,在性能上具有明显的优势。
ICM直接来源于哺乳动物的视觉皮层神经细胞研究成果,是从模拟哺乳动物的视觉活动中得到的人工神经元模型。ICM利用了生物神经元特有的线性相加,非线性相乘的调制耦合特性,同时考虑了哺乳动物的视神经系统的视野受到适当刺激时相邻神经元的同步脉冲发放特性。图1给出了一个基本ICM神经元结构图,其离散数学表达式为
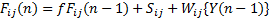 | (1) |
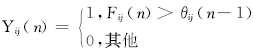 | (2) |
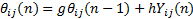 | (3) |
式中:下标 ij为各个像素点的坐标; Wij 为神经元之间的链接矩阵; Yij 为对应神经元的二值输出(1或0); Fij、 Sij、 θij 分别为神经元的树突状态值、输入图像对应像素值以及动态阈值; f、 g分别为对应迭代式的树突衰减系数和阈值衰减系数; h为阈值幅度常数, f、 g、 h均为标量系数,且满足g
同PCNN类似,ICM用于图像处理时对应为一个单层二维局部连接网络,其神经元个数与图像中像素点的个数一一对应。然而与同样具有生物学背景的经典PCNN模型不同的是,ICM摈弃了前者庞杂的链接输入分支和内部活动项产生机制,使得整个生物神经元模型的脉冲传播行为更为清晰,并在保留大脑视觉皮层模型有效性的同时大幅降低了计算复杂度。然而,ICM框架仍有自身的缺陷,表现如下:①迭代次数n如何恰当选取仍然是个难题。如果选取的参数n数值过小,则容易造成ICM神经元脉冲的非充分发放;相反如果迭代次数 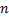
针对上述缺陷,本文对经典ICM进行了以下改进:①进一步简化连接调制器部分,忽略经典ICM中每一个神经元 ij对上一树突输入状态的记忆功能,仅保留外部输入 Sij 和上一迭代结束时的邻域内神经元二值整合信息;②对阈值函数 θ做出改进,将传统阈值衰减系数 g替换为单调递减的线性函数;③借鉴文献[ 9]中的思路,引入赋时矩阵 T用于自适应确定迭代次数,因为每个神经元的点火时间与点火频率更多地由与该神经元相链接像素的灰度值及其时间信息来决定,从而避免了参数 n的盲目选取。图2给出了IICM的神经元结构图。式(4)~式(7)对IICM神经元进行了数学描述。
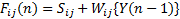 | (4) |
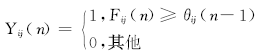 | (5) |
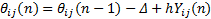 | (6) |
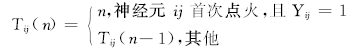 | (7) |
式(6)中,调整步长 Δ确保了各神经元动态阈值始终呈线性衰减趋势运行;阈值幅度常数 h通常给定为一个较大的数值,从而确保每个神经元的点火次数至多不超过一次,为式(7)中赋时矩阵的运行提供了前提。
式(7)中的赋时矩阵 T与神经元输出矩阵 Y大小相等,其元素 Tij 与 Yij相联系,记录了每个像素点的点火时间,并与IICM的神经元一一对应。有三个方面需要进行说明:①如果神经元 ij从未点火,则其对应的 Tij 值将始终为0;②若神经元 ij在某一次迭代时发生点火且为首次点火,则将 Tij 置为对应的迭代次数;③若神经元 i j发生点火但并非首次点火,则其对应的 Tij 值仍将保持首次点火时的迭代次数不变。由式(7)生成的赋时矩阵 T中,原处理图像中灰度变化较小的像素将具有相同或近似的点火时间,而IICM的连接调制器又对邻域内神经元的二值信息进行了整合处理,因此 
在实际的IICM参数设定过程中, S作为图像的外部输入值,通常为像素值,因此无需对其进行人工设定;链接权矩阵 Wij 直接决定了相邻神经元的输出脉冲对神经元 ij的影响程度,其通常取一尺寸为n×n的正方形区域,其中 n为不小于3的奇数,如果图像灰度分布和纹理比较单一, n可取较大一些的值。参数 Δ将决定阈值的线性衰减速率,在IICM中可取 Δ为6,阈值幅度常数 h用来限制每个神经元至多只点火1次,因而只需要将其赋予一个较大的数值即可满足要求,本文主要涉及256级灰度图像,故可将 h设为600。
本文对经典ICM进行了改进,IICM不仅拥有比前者更少且更为容易设置的参数个数,提升了算法运行效率,而且还可以根据图像处理的实际情况自适应地确定迭代次数 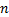
文中主要讨论的是双极脉冲噪声也称椒盐噪声。椒盐噪声可以是正的,也可以是负的。因为脉冲干扰通常比图像信号的强度大,因此,在一幅图像中,脉冲噪声总是数字化为最大值(纯黑或纯白)。由于这一结果,在灰度图像中,负脉冲常以一个黑点(胡椒点)出现在图像中。由于相同的原因,正脉冲则常以一个白点(椒盐点)出现在图像中。对于一个8位图像,这意味着0(黑)和255(白)。因此,在256级灰度图像中,受到脉冲噪声污染的像素点灰度值只有0和255两种取值。本文中除特别说明外,脉冲噪声均指双极脉冲噪声,灰度图像也均为256级灰度图像。
此外,当一幅图像受到外界脉冲噪声干扰时,可以直接通过观察各个像素点的灰度值估计整幅图片的受污染程度,但这种方法效率较低,且不够直观,本文提出的去噪方法是基于区域窗口的,因此可以设置一个区域,疑似污染系数 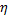
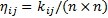 | (8) |
式中: kij 为以像素点 ij为中心的n×n区域窗口内各像素点对应的赋时矩阵元素值 Tij 等于1或等于整幅图像赋时矩阵最大元素值 Tmax 的像素点的个数,这种像素点被称为疑似污染像素点, n通常取奇数值。显然,0≤ ηij≤1。
结合IICM得出的赋时矩阵 T,如果像素点 ij对应的矩阵元素值 Tij 既不等于1、也不等于矩阵 T的最大元素值 Tmax,则表明像素点 ij的灰度值不等于0且不等于255,直接输出该像素点;如果 Tij 等于1或者等于矩阵 T的最大元素值,则认为像素点 ij为疑似污染像素点,此时若 ηij≠1,则对n×n区域窗口内非疑似污染像素点采用中值滤波,并将结果赋予最终图像;否则,若 ηij=1,则n×n区域窗口内所有像素点可能均受到脉冲噪声污染,此时需将区域窗口尺寸n×n扩展为(n+2)×(n+2),并再次检测 ηij,直至 ηij≠1,并对新生成区域窗口内非疑似污染像素点采用中值滤波,并将结果赋予最终图像。
基于IICM的自适应图像脉冲噪声去除算法的具体步骤如下:
输入:已被脉冲噪声污染、大小为 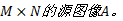
输出:经过基于IICM自适应图像脉冲噪声去除算法处理的最终图像 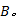
Step1 初始化赋时矩阵 T为一个大小为M×N的零矩阵,由1.2节中式(4)~式(7)来得出源图像 A的赋时矩阵 T,并得出 T中元素的最大值 Tmax;
Step2 根据赋时矩阵 T计算源图像A中各像素点的区域疑似污染系数 ηij,其中1≤i≤ M,1≤ j≤ N;
Step3 对赋时矩阵 T中的元素 Tij,选取n×n的区域窗口进行元素取样;
(a)若 Tij 的n×n区域窗口内, Tij 满足 Tij≠1且 Tij≠ Tmax,则在最终图像 B中保持原像素点灰度值 Aij 不变,即 Bij= Aij,转Step4;
(b)若 Tij的n×n区域窗口内, Tij满足 Tij=1或 Tij = Tmax,则源图像 A中像素点 Aij为疑似污染像素点,此时若 ηij≠1,则对n×n区域窗口内非疑似污染像素点采取中值滤波,并将结果赋予图像像素点 Bij,转Step4;
(c)若 Tij的n×n区域窗口内, Tij满足 Tij=1或 Tij= Tmax,则源图像 A中像素点 Aij为疑似污染像素点,此时若 ηij=1,则将n×n区域窗口尺寸扩展为(n+2)×(n+2),再次计算 ηij,若 ηij≠1,则对新区域窗口内非疑似污染像素点采取中值滤波,将结果赋予图像像素点 Bij,转Step4;否则继续对原区域窗口进行扩展,直至满足 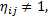
Step4 若T中所有元素 Tij处理完毕,算法结束;否则返回Step3。
为了验证本文方法的合理有效性,利用Matlab7.1软件,对标准测试图像Lena,Peppers进行脉冲噪声处理仿真实验,上述图像均为已配准的256级灰度图像,图像大小为512×512像素。
本文将采用近年来性能较为优越的5种去噪方法与本文方法(A6)进行比较:3×3的经典标准中值滤波法MEDF(A1)、基于PCNN的图像去噪法[ 9](A2)、文献[ 14]的图像去噪法(A3)、文献[ 15]的图像去噪法(A4)以及文献[ 16]的图像去噪法(A5)。A2~A5中的参数均按照原对应文献中的给定数据设定,本文方法的链接权矩阵 W设置为[0.707,1,0.707;1,0,1;0.707,1,0.707], Δ为6,阈值幅度常数 h设为600。
对于图像的去噪效果可以采用主观评价的方式进行,但由于主观评价往往容易受到评价者视觉特性、心理状态等因素的影响,因而,本文采用常用的均方误差和峰值信噪比评价参数作为定量的评价标准。
(1)均方误差(Mean square error,MSE)用来评价处理后图像与源图像之间的差异程度。MSE值越小,表明处理前后图像越接近,处理效果越好,其理想值为0。其表达式为
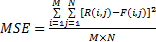 | (9) |
式中:(i,j)为图像的像素点坐标; F为源图像; R为噪声处理后的图像;M×N为图像的大小。
(2)峰值信噪比(Peak-to-peak signal-to-noise ratio,PSNR)是图像像素之间均方误差的对数分贝表示,它能在一定程度上反映图像数据处理前后的变化情况以及数据变化前后噪声是否得到了有效抑制。PSNR值越大说明去噪效果越好,处理后的图像质量越高。其表达式为
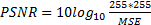 | (10) |
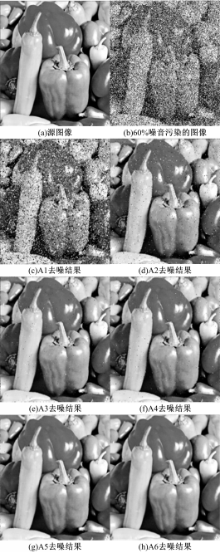
以512×512的标准Lena、Pepper图作为原始图像,分别加入10%、20%、30%、40%、60%的脉冲噪声,并采用A1~A6进行对比,所有方法均以峰值信噪比PSNR和均方误差MSE作为性能优劣的评价标准,实验数据如表1、表2所示。6种算法的去噪效果如图3和图4所示。
| 表1 Lena图像的去噪方法实验数据 Table 1 Statistics of anti-noise methods of Lena image |
| 表2 Pepper图像的去噪方法实验数据 Table 2 Statistics of anti-noise methods of Pepper image |
从直观角度看,上述6种方法均取得了比较好的图像去噪处理效果,但比较后发现,A1去噪效果最差,其对应的去噪图像仍分布有大量的脉冲噪声点,严重干扰了视觉效果。A2虽然相比A1的脉冲噪声点大幅减少,但整幅图像的受污染情况仍比较严重,此外,A2是基于PCNN的图像去噪方法,大量待定参数和迭代次数的设置问题也制约了去噪效果的进一步提升。A3~A6效果较好,不仅滤除了绝大部分的脉冲噪声,还较好地保持了源图像的重要特征和细节信息。但通过比较不难发现,同A3~A5相比,A6算法更彻底地滤除了源图像中加入的脉冲噪声,残留脉冲噪声点存在的最少,源图像特征信息保留的也最完整,不仅如此,A6还具有更为合理的亮度水平。
此外,直观视觉效果在客观评价指标数据中也得到了验证,根据表1、表2提供的客观评价数据,可以发现在纵向角度上,同其他5种去噪方法相比,随着脉冲噪声密度的增大,本文算法PSNR指标的下降和MSE指标的上升较为缓慢,体现出优越的鲁棒性;从横向角度观察,尽管当噪声密度较低时,本文算法同其他方法的指标值相差并不是很大,而且去噪效果也几乎相当,但随着脉冲噪声密度的逐渐增大,尤其是超过了50%以后,其余方法的指标值发生了异常剧烈的变化,而本文方法的PSNR和MSE两项指标值变化却相对平缓得多,同时,源图像脉冲噪声密度越大,本文方法对应的两项指标值与其余几种方法相比,其优势就越明显。
对经典ICM理论进行了改进,提出一种基于IICM的自适应图像去噪方法。IICM对经典ICM的参数设置机制进行了大幅改进,并引入赋时矩阵自适应地确定迭代次数。提出了IICM的自适应图像去噪算法,该算法仅对受污染的像素点进行处理,最大程度地保留了源图像的边缘细节信息,此外,它还可根据待去噪图像的受污染程度自适应地确定去噪区域窗口的尺寸,摒弃了以往算法中去噪区域窗口的单一化固定设置模式。仿真实验表明:本文提出的图像去噪算法具有比以往经典去噪算法更为优越的脉冲噪声滤除性能。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|