引用本文
李欢利, 郭立红, 王心醉, 李小明, 董月芳, 方艳超. 基于加权Gabor滤波器的虹膜识别. 2014, 44(1): 196-202[LI Huan-li, GUO LI-hong, WANG Xin-zui, LI Xiao-ming, DONG Yue-fang, FANG Yan-chao. Iris recognition based on weighted Gabor filter. 吉林大学学报(工学版), 2014, 44(1): 196-202]  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于加权Gabor滤波器的虹膜识别
李欢利1,2, 郭立红1, 王心醉3, 李小明4, 董月芳3, 方艳超1
1.中国科学院 长春光学精密机械与物理研究所,长春 130033
2.中国科学院大学,北京 100039
3.中国科学院 苏州生物医学工程技术研究所,江苏 苏州 215163
4.中国航空工业集团公司 洛阳电光设备研究所,河南 洛阳 471023
郭立红(1964),女,研究员,博士.研究方向:计算机应用.E-mail:guolh@ciomp.ac.cn

李欢利(1986),女,博士研究生.研究方向:图像处理.E-mail:lihl483@sina.com

基金:国家自然科学基金项目(51205268);
中图分类号:TP391.4 文献标志码:A 文章编号:1671-5497(2014)01-0196-07
Iris recognition based on weighted Gabor filter
LI Huan-li1,2, GUO LI-hong1, WANG Xin-zui3, LI Xiao-ming4, DONG Yue-fang3, FANG Yan-chao1
1.Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033,China
2.University of Chinese Academy of Sciences, Beijing 100039,China
3.Suzhou Institute of Biomedical Engineering and Technology, Chinese Academy of Sciences, Suzhou 215163,China
4.Luoyang Institute of Electro-Optical Equipment of AVIC, Luoyang 471023,China
Fund:
Abstract

In order to improve recognition rate of the iris recognition system, the Gabor filter is studied, and the weighted Hamming distance based on analytic hierarchy process is proposed. First, the feature image is generated through different scales and directions of the odd symmetric Gabor filter. Then, the recognition correct rate and error rate are acquired by Hamming distance matching. The appropriate scale and direction are selected to calculate the weighted Hamming distance. The weight is calculated by analytic hierarchy process. Finally, the weighted Hamming distance is used to iris recognition. The equal error rate of CASIA2.0 and MMU1 are decreased by 0.64% and 0.56%, respectively. The experimental results show that this method has better recognition performance and robustness.

Keyword: computer application; iris recognition; Gabor Filter; Hamming distance; analytic hierarchy process

常见的生物识别技术有:指纹识别、掌纹识别、人脸识别、视网膜识别、虹膜识别、DNA识别等。由于虹膜具有天然防伪性、唯一性、非侵犯性、稳定性等特征,近年来得到了学术界的广泛关注[ 1]。

Daugman[ 2]用Gabor滤波器方法提取出虹膜纹理的相位特征,用Hamming距离进行匹配分类;Wildes等[ 3]用金字塔分解的方法提取特征,并用图像间的相关性进行匹配分类;Boles等[ 4]用小波过零点检测提取特征的方法,采用过零点数目一致,根据相关性进行匹配分类。以上方法均取得了很好的效果,但是相对Daugman的算法并没有很大的改善,所以基于多尺度Gabor滤波器方法和Hamming距离匹配方法应用范围相对较广。以往的方法计算Hamming距离时对不同的Gabor滤波器的结果同等对待,但是,根据虹膜图像纹理的特性分布,不同尺度、方向、实部、虚部的Gabor滤波器对其的描述能力不同[ 5, 6],在计算Hamming距离时应区别对待[ 7]。

本文在深入研究Gabor滤波器和层次分析法的基础上,提出了基于加权Hamming距离的虹膜识别算法。首先,根据实部偶对称、虚部奇对称Gabor滤波器的特性,采用不同尺度和方向的虚部奇对称Gabor滤波器对虹膜库进行识别;然后,根据等错率(EER)和最高正确识别率(CRR)选取合适的尺度和方向的Gabor滤波器,采用基于加权Hamming距离进行虹膜识别,其中,权值的计算采用层次分析法;最后,用本文方法对不同的虹膜库进行识别,实验结果表明,该方法能够有效降低等错率。

1 虹膜图像的预处理与匹配

虹膜图像的预处理包括虹膜的定位、归一化和增强[ 8]。虹膜是介于黑色瞳孔区域和白色巩膜区域之间的环形区域,两者均接近于圆形,虹膜的定位就是找到这个环形区域的圆心并确定其半径。目前广泛使用的归一化方法为Daugman教授提出的橡皮圈(Rubber-sheet)模型[ 9],该模型把虹膜假设为一个具有柔韧性和各向同性的弹性模型,将环形的虹膜区域线性展开为一个具有固定大小的矩形区域。

图1为虹膜定位和归一化的结果。归一化后的图像左半部分容易受到睫毛和眼睑遮挡,上面容易受到瞳孔的影响,为了提高计算速度和识别准确率,本文舍弃靠近瞳孔的四行像素,取右上面大小为32×256像素的区域,该部分有清晰的纹理,可代表虹膜图像的特征。虹膜的归一化使其具有了平移不变性和尺度不变性。

图1 虹膜的定位和归一化Fig.1 Result of iris localization and normalization

由于拍摄虹膜图像时,头部的倾斜会造成虹膜图像的旋转,需使虹膜具有旋转不变性[ 6]。旋转不变性对应于归一化后图像的水平移位;所以旋转不变性可通过水平移位来消除。

设I和J分别为两个不同虹膜图像的特征编码,则它们间的Hamming距离[ 2]为

(1)

式中:N为图像编码的总位数;􀱇为异或关系运算。

当Ii与Ji相同的时候异式运算为0,不同的时候为1,相同虹膜的编码相似,且Hamming距离小,不同虹膜的编码则有很大的差异,且Hamming距离大,故可以用Hamming距离作为标准来区分两幅虹膜图像是否为同一虹膜。

在水平移位匹配中,对识别图像进行向左、向右各平移20个像素,共移位40个像素,即旋转-14.0625°~14.0625°。

对于虹膜定位不太精确造成的垂直方向的差异,通过垂直方向移位匹配方法消除。本文对在水平移位匹配过程中取得最小值的位置进行-3~3个像素的垂直移位匹配,如果此时的值小于匹配向量中的最小值,用之替换。

ROC曲线是表示错误拒绝率(FRR)与错误接受率(FAR)关系的曲线,反映了整个系统的匹配性能,ROC曲线越接近纵、横坐标轴,表明系统性能越好。EER为FRR和FAR相等时候的值,EER越小,系统性能越好。本文用ROC曲线、EER来评价算法的好坏。

2 Gabor滤波器与层次分析法
2.1 方法简介

二维复数Gabor的一般形式为

(2)

式中: 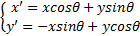σx、σy为滤波器的尺度参数;f为频率;θ为方向。

Gabor滤波器可以分解为实部偶对称和虚部奇对称的两个滤波器:

(3)

(4)

它们的时域波形(θ=0)如图2所示。

图2 Gabor滤波器的时域波形Fig.2 Gabor filter waveform in time domain

可将二维Gabor滤波器作为θ方向的带通滤波器,垂直方向上的低通滤波器,改变f和θ可以很好地提取出与此相对应的纹理信息,因此非常适合于提取出虹膜的纹理特征进行虹膜识别。

Daugman[ 2]对虹膜图像经过Gabor复小波处理后,提取出局部相位信息作为虹膜的纹理特征,然后对特征点进行编码,这种方法可以分解成两个部分,即实部偶对称滤波器和虚部奇对称滤波器。如果处理后的幅值大于0,则编码为1,否则为0。

综上所述,可以对虹膜进行两部分的编码,一部分为经过实部偶对称滤波器(见式(3))的编码,一部分为经过虚部奇对称滤波器(见式(4))的编码。文献[ 5, 6]证实了实部偶对称Gabor滤波器不适用于提取虹膜的纹理信息,用它来提取特征时也将降低系统的识别性能,单独采用虚部奇对称Gabor将会达到更好的性能。但是文献[5-6]中并没有分析不同f和θ时的识别效果。

2.2 参数的选取

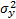
σx、σy为Gabor滤波器窗口的尺度因子,它们决定了滤波器的作用范围。令式(2)中的x'/ +y'/ =u2,则 exp(x'/ +y'/ )= exp{-u2},绘制 exp{-u2}的曲线如图3所示,可以看出,随着u值的增大, exp{-u2}的值迅速减小,并接近于0,当u≥2时函数值变化很小,衰减超过了98.168%[ 6];因此本文取u=2。

图3 exp(- u2)随着 u值的变化Fig.3 exp(- u2) varying with value of u

σx、σy与频率f的关系如式(5)所示,其中n为滤波器窗口中含有波长的个数。

(5)

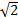
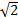
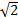
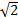
为了分析不同滤波器参数对虹膜识别结果的影响,本文设置以下参数:①根据滤波器的奇对称性,方向θ选取为0°、45°、90°、135°;②本文取n=1,u=2。当频率f取0.125、0.0625、0.0417、0.03125时,尺度σx=σy为 、2 、3 、4 。

当θ=0°,f=0.125,σx=σy= 时,其滤波器图像如图4所示。文献[ 5, 6]中对虹膜图像进行滤波时,将整个滤波器范围都考虑进去了,而实际上,远离中心像素点的位置将会为纹理的提取带来噪声,影响识别效果,因此本文中滤波器范围只选取到最大值的位置。例如:对图4中的滤波器,最终选取的滤波窗口为5×5大小。

图4 当 θ=0 °, f=0 .125, σ x =σ y= 时的滤波器图像Fig.4 Filter image when θ=0 °, f=0 .125, σ x =σ y=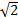

为了证实上述选取滤波窗口的有效性,本文采用上述4个尺度、方向的滤波器,分别对CASIA1.0虹膜库进行识别,最高正确识别率(CRR)和等错率(EER)结果如表1所示。

表1 不同尺度、方向滤波器结果 Table 1 Filter result of different scales and directions

从表1中可以看出,除了(0°,0.125)和(90°,0.125)的滤波器外,本文选取的滤波窗口均取得了更好的效果。

文献[ 5, 6]对不同滤波器得到的Hamming距离进行同等对待,这样不一定能够提高系统的识别性能。从表1中可以看出,当采用0°滤波器时可以获得很高的识别率,而用90°滤波器时效果却很差,这是由虹膜图像的纹理决定的。

文献[ 7]提出了根据不同滤波器的鉴别能力对每个滤波器的输出进行加权,而权重大小的设置是人为的,但是其基本原则是:错误识别率越小的滤波器获得的权重越大。

从表1中可以看出,同一方向不同尺度的滤波器的识别性能相差不大,所以本文选取每个方向取得最好效果的尺度组成滤波器,同时由于90°方向的滤波器的识别性能太差,不予考虑。所以本文选取(0°,0.0625)、(45°,0.125)、(135°,0.0625)三个滤波器进行加权识别。

2.3 层次分析法

层次分析法(Analytic hierarchy process,AHP)将与决策有关的因素分解成目标、准则、方案等层次,然后再进行定量和定性的分析[ 10]。主要分为以下四步进行:

(1)分析系统中各个因素之间的关系,建立起系统的层次结构。

层次结构分为三类:①最高层即目标层,这一层只有一个元素,为问题的预定目标;②中间层又称准则层,包括为了实现目标所涉及的中间环节,可有若干个层次组成;③最底层是为了实现目标可供选择的各种措施和方案,又称为方案层。

层次结构模型的层次数一般不受限制,但是每个层次中可支配的元素一般不要超过9个,如果超过9个,可将该层次再次划分为若干子层。

(2)对同一层次的各个元素关于上一层中某一准则的重要性进行比较,构造两两比较判断矩阵。

针对某层来说,使用数量化的相对权重aij来表示第i个元素与第j个元素相对某层的重要性,构成判断矩阵。

在决策者心中,各个元素占有一定的比例,一般使用1~9及其倒数作为标度来确定判断矩阵的值。1~9的比例标度如下:i比j强的重要程度 a ij=1(相等)、3(稍强)、5(强)、7(很强)、9(绝对强)。其中2、4、6、8分别介于1、3、5、7、9对应的重要程度之间。

(3)由判断矩阵计算被比较元素相对于该准则的相对权重和一致性检验。

首先,计算一致性指标 CI, CI= ,其中λ max为判断矩阵的最大特征值。然后查表得到平均随机一致性指标RI,如表2所示,最后,计算一致性比率CR,CR=CI/RI。当CR<0.1时,认为判断矩阵满足一致性,否则,应修正判断矩阵。

表2 不同阶数矩阵的随机一致性指标 Table 2 Rondom consistency index of different order matrix

(4)计算各层次元素对系统目标的合成权重并排序。

最终需要得到各个元素(尤其是最底层中各个元素)对目标的排序权重。对层次总排序进行一致性检验,计算出各层元素对总目标的合成权重,最终对各个备选方案排序。

2.4 层次分析法加权Hamming距离虹膜识别

本文设置的层次结构模型如图5所示。

图5 层次结构模型Fig.5 Hierarchical structure model

根据EER和CRR的值,通过大量的实验,本文设置如下判断矩阵:

(6)

根据2.3节的步骤,得到的权值分别为0 .7146、0 .2004、0 .0850

利用上述权值对每个滤波器的 Hamming距离进行加权。对 CASIA1 .0虹膜库,其中0 °滤波器、均值加权、层次分析法加权的 ROC曲线如图6所示: CRR和 EER如表3所示,可以看出本文方法在提高 CRR的同时降低了 EER。

图6 CASIA1.0库不同方法的ROC曲线比较Fig.6 ROC curve comparison among different methods on CASIA1.0

表3 不同方法下CASIA1.0库的CRR和EER Table 3 CRR and EER of CASIA1.0 using different methods
3 实验结果与分析

本文对中国科学院自动化研究所的CASIA1.0、CASIA2.0、CASIA3.0-Interval、MMU1虹膜库进行识别。实验环境如下:CPU为Pentium(R)E5500(主频2.80 GHz),内存3 GB,操作系统为Windows XP,使用的软件为Matlab7.8。

在2.4节中,通过在CASIA1.0图像库上的实验选取了滤波器和权值,为了验证本文方法的鲁棒性,在遮挡比较严重的CASIA2.0库、图像数量较大的CASIA3.0-interval库、包含不同种族和年龄人群的MMU1库上进行了实验。

每个图像库的类内、类外、总匹配次数如表4所示。

表4 不同数据库的匹配次数 Table 4 Match number of different iris database

对CASIA2.0库采用0°滤波器、均值加权、层次分析法加权的ROC曲线如图7所示,CRR和EER如表5所示,其中45°滤波器和135°滤波器权值和CASIA1.0数据库下的对调。

图7 CASIA2.0库不同方法的ROC曲线比较Fig.7 ROC curve comparison among different methods on CASIA2.0

表5 不同方法下CASIA2.0库的CRR和EER Table 5 CRR and EER of CASIA2.0 using different methods

对CASIA3.0-interval库采用0°滤波器、均值加权、层次分析法加权的ROC曲线如图8所示,CRR和EER如表6所示。

图8 CASIA3.0-interval库不同方法的ROC曲线比较Fig.8 ROC curve comparison among different methods on CASIA3.0-interval

表6 不同方法下CASIA3.0-interval库的CRR和EER Table 6 Highest CRR of CASIA3.0-interval using different methods

对MMU1库中的图像采用0°滤波器、均值加权、层次分析法加权的ROC曲线如图9所示,CRR和EER如表7所示。其中45°滤波器和135°滤波器权值和CASIA1.0数据库下的对调。

图9 MMU1库不同方法的ROC曲线比较Fig.9 ROC curve comparison among different methods on MMU1

表7 不同方法下MUU1库的CRR和EER Table 7 CRR and EER of MUU1 using different methods
4 结束语

本文对Gabor滤波器和层次分析法进行了研究,提出了基于加权Hamming距离的虹膜识别算法。首先,选取合适的滤波器;然后,采用层次分析法进行权值的计算;最后,采用基于加权Hamming距离进行虹膜识别。实验结果表明,在包含不同种族和年龄的MMU1虹膜库上的EER下降了0.56%;在遮挡比较严重的CASIA2.0虹膜库上EER下降了0.64%。可以看出本文算法具有很好的鲁棒性,安全性好,且算法易于实现,具有较好的应用价值。

The authors have declared that no competing interests exist.

Reference
[1] 王蕴红, 朱勇, 谭铁牛. 基于虹膜识别的身份鉴别[J]. 自动化学报, 2002, 28(1): 1-10.
Wang Yun-hong, Zhu Yong, Tan Tie-niu. Biometrics personal identification based on iris pattern[J]. Acta Automatic Sinica, 2002, 28(1): 1-10. [Cited within: 1]
[2] Daugman J. High confidence visual recognition of persons by a test of statistical independence[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1993, 15(11): 1148-1161. [Cited within: 3] [JCR: 4.795]
[3] Wildes R, Asmuth J, Green G, et al. A machine-vision system for iris recognition[J]. Machine Vision and Applications, 1996, 9(1): 1-8. [Cited within: 1]
[4] Boles W W, Boashash B. A human identification technique using images of the iris and wavelet transform[J]. IEEE Transactions on Signal Processing, 1998, 46(4): 1185-1188. [Cited within: 1] [JCR: 2.813]
[5] 姚鹏, 叶学义, 张文聪, 等. 基于改进的Log-Gabor小波的虹膜识别算法[J]. 计算机辅助设计与图像学学报, 2007, 19(5): 563-568.
Yao Peng, Ye Xue-yi, Zhang Wen-cong, et al. Iris recognition using modified Log-Gabor wabelets[J]. Journal of Computer-aided Design & Computer Graphis, 2007, 19(5): 563-568. [Cited within: 4] [JCR: 3.172]
[6] 程宇奇. 用于身份鉴别的虹膜识别方法研究[D]. 长春: 中国科学院长春光学精密机械与物理研究所, 2010.
Cheng yu-qi. Research on iris recognition algorithms for personal identification[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Science, 2010. [Cited within: 6]
[7] 冯薪桦, 丁晓青, 吴佑寿. 基于加权Hamming距离的虹膜匹配算法[J]. 清华大学学报: 自然科学版, 2009, 49(4): 514-517.
Feng Xin-hua, Ding Xiao-qing, Wu You-shou. Iris matching algorithm based on weighted Hamming distance[J]. J T singhua Univ(Sic&Tech), 2009, 49(4): 514-517. [Cited within: 2]
[8] 程宇奇, 朱明, 李桂菊, 等. 应用迭代圆环像素率法实现快速虹膜定位[J]. 光学精密工程, 2010, 10(10): 2306-2313.
Cheng Yu-qi, Zhu Ming, Li Gui-ju, et al. Rapid iris localization based on method of iterative pixel ratio to cirque area[J]. Opt Precision Eng, 2010, 10(10): 2306-2313. [Cited within: 1]
[9] Daugman J. How iris recognition works[J]. IEEE Transactions on Circuitsand Systems for Video Technology, 2004, 14(1): 21-30. [Cited within: 1]
[10] 邓雪, 李家铭, 曾浩建, 等. 层次分析法权重计算方法分析及其应用研究[J]. 数学的实践与认识, 2012, 42(7): 93-100.
Deng Xue, Li Jia-ming, Zeng Hao-jian, et al. Research on computation methods of AHP weight vector and its applications[J]. Mathematics IN Pracrice and Theory, 2012, 42(7): 93-100. [Cited within: 1]