郭栋梁(1983),男,讲师,博士后.研究方向:虚拟现实,计算机仿真.E-mail:dongliangguo@ysu.edu.cn
针对多尺度规则网格模型在不同层次细节过渡时易产生几何不连续的问题,分析基于GPU裂缝处理的LOD架构,提出一种参数化处理裂缝的思想,利用曲线函数控制不同LOD过渡时的网格顶点布局,消除因层次细节过渡产生的T型连接,并扩展至消除多跨度LOD裂缝。最后将该裂缝处理方法应用于当前两种常见多尺度规则网格的LOD模型中。通过实验分析表明,本文方法在保证网格平滑过渡的同时,有效地提高了裂缝处理速度。
方法
When using level-of-detail (LOD) technology, multi-scale regular grid visualization always introduces discontinuous mesh on the boundary with different resolutions. The GPU-based LOD framework for cracks repairing is investigated, and a parameterization method to avoid cracks is proposed. The function curve fitting is employed to change the mesh layout and eliminate T-junctions caused by various LODs transiting. Moreover, the parameterization cracks-repairing method supports multi-span LOD using curve function family excellently. Function curve fitting method is utilized to existing regular-grid-based LOD model. The experiments show that the proposed method can improve the cracks-repairing performance meanwhile guarantee the mesh continuity.
与不规则网格相比,规则网格表现三维模型表面具有数据处理简单高效、压缩率高和适合硬件加速等特点,规则网格层次细节(LOD)可视化技术[ 1, 2]一直是计算机图形图像研究的热点问题,规则网格数据绘制技术广泛应用于科学可视化、虚拟现实、地理信息科学、游戏娱乐等领域。然而随着数据获取和处理技术的发展,各种形式的规则网格三维数据规模越来越大,计算机已难以实现对其原始精细数据的实时三维可视化,需使用LOD技术[ 3, 4, 5]进行规则网格模型多尺度处理。
实现模型的多尺度网格平滑过渡,需要解决的一个关键技术问题就是避免不同层次边缘处产生的“裂缝”现象。目前消除网格间裂缝的方法主要有:添加/移除几何顶点、添加过渡带、裙边和0区三角形等。这些方法虽在一定条件下能满足无裂缝的视觉效果,但需对网格区域进行复杂的控制和额外的几何计算,降低了LOD模型绘制的实时性和自适应性。为此,本文提出多尺度规则网格裂缝处理参数化的思想,利用曲线函数控制几何顶点,在GPU上对引起裂缝的顶点进行偏移,从而平滑网格层次间的裂缝。该方法主要优点如下:①简单:输入网格类型为单一规则网格,不会引入以往处理裂缝所必须的辅助几何网格;②高效:曲线拟合处理过程完全在GPU上实现,实现了裂缝处理硬件加速;③易用:能应用于多种常用规则网格LOD模型,如Chunked LOD、GeoMipmaps、Clipmaps等;④灵活:能够通过多种曲线函数来调节裂缝修补的效果。
规则网格LOD模型可分为细粒度简化和粗粒度简化两类:细粒度简化[ 6, 7]以每个三角形为单位对网格进行简化,虽然能精确控制绘制面片规模,但频繁的面片调度使其很难利用GPU硬件加速功能;粗粒度简化将三角形集作为基本单位进行简化处理,使用硬件支持的三角形批绘制技术实现模型快速绘制。由于可以利用高性能GPU进行加速计算和绘制,基于粗粒度简化的模型成为近年来大规模三维数据可视化的主要绘制架构。
实现粗粒度规则网格LOD模型的关键难点就是解决多尺度网格连续性问题。由于层次结构不同,粗粒度简化模型又可以分为基于直角三角形划分的二叉树结构和基于正方形划分的四叉树结构。Gobbetti等[ 8]、Lindstrom等[ 9]和Bosch等[ 10]分别继承了三角形二叉树[ 6]结构,以直三角区域作为绘制单元,绘制时利用斜边剖分来保证边界网格连续,隐式地避免了裂缝的出现,但仅适用于相邻三角形区域的层次细节度不超过1的情况,无法保证多跨度LOD下的网格连续性。
对于基于正方形划分的四叉树结构,Wagner[ 11]利用在低层次区域加入顶点的方式避免T-连接,Koomia等[ 12]则通过移除高层次区域边界顶点的方式实现平滑过渡,添加或删除顶点虽能消除网格的不连续,但也会降低绘制单元的规整性,易于在CPU上实现,很难利用GPU加速。为获得硬件加速,Livny等[ 13]和Asirvatham等[ 3]在不同层次的相邻区域间加入过渡区域来显式处理区域间裂缝,虽在一定程度上提高了绘制效率,但其需穷举多种类型绘制单元来填充过渡区域,增加了裂缝处理的复杂度。Roberts等[ 14]使用0型区的方式来避免裂缝,可见与之类似,Ulrich[ 1]、Wahl[ 15]、Schneider[ 16]和Dick[ 17]均通过在区域块间加“裙边”来避免裂缝可见,但这类方法从拓扑关系上无法保证网格连续,适用于2.5维地形数据模型,却无法支持基于位移贴图和几何图像的三维网格模型。
GPU性能的飞跃促进了基于GPU的裂缝实时处理技术的发展。2009年Strugara[ 18]提出“LOD Morph”方法,对引起T-连接的顶点进行操作,通过控制网格内部顶点等比例偏移,实现LOD平滑过渡。顶点偏移在顶点着色器上实现,虽提高了绘制效率,但对区域网格内部顶点的过多偏移却导致了网格表面变形,并产生大量尖锐三角形。
为保证粗粒度规则网格LOD模型的几何连续性,本文以基于GPU的顶点偏移为技术基础,提出使用曲线函数拟合方法实现LOD间的平滑过渡,在GPU上控制顶点有规律地偏移,提高了绘制效率,增强了模型可视化质量,适用于处理多种规则网格多尺度模型的裂缝问题。
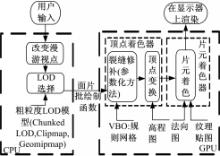
首先将输入的规则网格几何数据以顶点缓存对象(Vertex buffer objects,VBO)的形式,把位置、色彩和法向等绘制相关数据以纹理的形式存储在显存上。绘制前先执行几何块LOD选择,然后通知VBO对需要绘制的几何块进行渲染。在渲染阶段,为保证网格连续性,在顶点着色器中首先对顶点进行位置偏移操作,然后根据偏移后的顶点位置,从位移贴图、颜色贴图和法向贴图中提取实际的位置、色彩和法向信息。如图1所示,这种LOD架构的优点在于,粗粒度的LOD选择和简单的几何绘制单元可以有效地避免CPU-GPU间的数据传输,减少CPU的计算负载。
以往的裂缝消除方法,是把引起裂缝的顶点区域作为控制目标,分析相邻区域间层次衔接关系,通过添加几何网格、删除T型顶点或在粗糙层网格强制添加顶点来实现。这些方法均改变了规则网格的布局,导致网格的规则性被破坏,致使裂缝修补复杂化,很难在如GPU这样的单指令流多数据流(Single instruction multiple data,SIMD)架构的硬件上获取高处理性能。由于引起多尺度规则网格T型裂缝的顶点具有等间隔、共行列的特性,移动此类顶点至最近的网格块共享顶点,保证了网格的顶点规则性,即能修复网格间裂缝,实现几何模型网格的平滑绘制。本文提出的函数曲线拟合方法,即利用特殊函数控制所有网格顶点的偏移来消除T型顶点,避免以往方法弥补裂缝引入的额外几何数据和复杂处理,便于利用GPU进行加速。
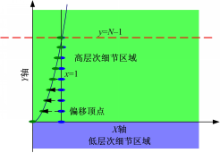
曲线函数拟合目标是移动T型顶点到距之最近、层次间共享的顶点位置处。如图2所示,定义如下坐标系:含有最近共享顶点的列方向为Y轴方向,共享边所在方向为X方向,顶点间间距为坐标系单位长度,X轴上半区为高细节区域,下半区为低细节区域,则控制顶点所在的初始曲线为x=1,假设目标曲线函数x=f(y),那么只要该函数满足0=f(0)且1=f(N-1)即可,其中N是每列的顶点数,即函数曲线通过(0,0)和(1,N-1)点,那么就能避免不同层次块之间的T型连接。以上列举的是高细节区域底部裂缝处理的情况,由于关于y=(N-1)/2对称,顶部裂缝处理的曲线函数即为x=f(N-1-y),同理,左部和右部的情况可以使用y=f(x)和y=f(N-1-x)来处理,因此本文只对底部裂缝处理进行阐述,其他三种情况类似。某些函数类型,如分段函数、线性函数、幂函数和三角函数,通过对函数参数的设置,即能达到曲线拟合消除裂缝的要求,且很容易在顶点着色器上实现。
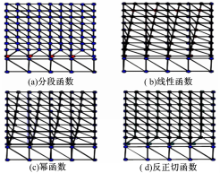
分段函数是最直接的曲线形式,通过分段函数控制所有网格顶点,而实际只有T型顶点进行偏移,如图3(a)所示,在函数x=1中,只有y=0点被移动,其函数形式为
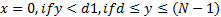
式中:参数 d取值范围为区间(0,1)的任意值。
图3(a)中,由于分段函数只移动了T型顶点,对网格布局进行了最小化改变,因此保证了表面细节损失最小。
线性函数定义形式为 x= ky,且通过(0,0)和(1, N-1)点。该网格布局如图3(b)所示,与Strugara[ 18]提出的CDLOD算法非常相似。线性曲线解决裂缝形式简单,只需做一次乘法运算,但同CDLOD算法一样,控制列中所有顶点均偏移,将引起原始网格表面特征变化,且由于实际网格数据列中顶点数一般都在100数量级,导致列间距相对较窄,并产生许多尖锐三角形,影响绘制质量。
作为线性函数曲线表面质量的扩展改进方法,幂函数曲线形式定义为 y=(N-1)xn 。幂函数改变原始数据表面效果如图3(c)所示,幂系数 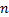
能高效、保真地解决裂缝的函数曲线应该具有以下特性:当y≤1时,曲线能够从原点(0,0)处快速接近(1,1)点;当y>1时,曲线缓慢地靠近x=1直至贯穿(1,N-1)点。三角函数中的反正切函数具有类似特性,当y≤1时,曲线快速靠近(π/4,1)点;当y>1时,曲线无限缓慢靠近x=π/2,直到趋向(π/2,+∞)。因此,函数y=ktan(ax),即 
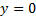
多跨度LOD裂缝指尺度差别大于1个层次的网格不连续现象。对于增删顶点和过渡区域的裂缝解决方式,增加相邻块间层次细节度差距意味着增加额外的判断或穷举修补处理。为简化裂缝处理,一般使用约束将相邻块间层次细节度差距控制在1之内,但细节约束会引起不必要的面片细节绘制,加重绘制规模。
假设目前渲染区域块的细节层次为l,其底部邻居的层次细节度为 lb,且 lb≤l,则此相邻层次间网格跨度 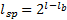
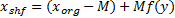 | (1) |
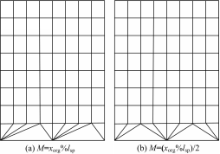
式中: xorg和 xshf分别表示顶点偏移前、后的 x坐标值,跨度系数 M=xorg/ lsp。图4(a)为 lsp=4时使用曲线函数族修补裂缝的效果。为了保持几何对称,改善网格布局效果,可设定 M=( xorg% lsp)/2来移动参考Y轴,将参考Y轴作为函数族的对称轴,裂缝修补效果如图4(b)所示。
曲线函数拟合参数化方法解决裂缝问题,适用于当前多种基于多尺度规则网格的LOD模型,如Clipmaps、Chunked LOD和GeoMipMaps等。应用时只需分析LOD节点间关系,用曲线函数拟合替代原有解决裂缝的方法并在顶点着色器上执行即可,因此有较强易用性。
图5展示了传统Clipmaps和基于本文方法的Clipmaps几何块布局方式的对比效果。为保证网格连续性,Asirvatham[ 3]使用12个正方形网格块、4个环修复块、2个内饰网格块来表示整个Clipmap环,并使用4个外部退化三角形条带遮挡环间裂缝(见图5(a))。相比之下,如图5(b)所示,调整后的Clipmaps结构只用一类12个正方形网格块表示Clipmaps环,覆盖图元更简单、绘制规模更小。
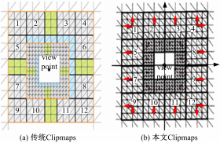 | 图5 传统Clipmaps模型和基于曲线函数拟合解决裂缝的Clipmaps的网格布局对比效果Fig.5 Comparison of meshes layouts between original Clipmaps and our Clipmaps with function curve fitting |
在基于曲线函数拟合解决裂缝的Clipmaps中,每个网格块的上下或左右邻居不会存在分辨率同时比本块低的情况。为了更直观地反映这一特性,在图5(b)中使用箭头方向代表层次细节度低的邻居节点的方向,由于Clipmaps模型的层次细节由内到外是依次递减的,因而网格布局中不可能出现上下方向或左右方向上有双箭头的现象。设参数dbu和dlr分别代表几何块在垂直、水平方向上的箭头朝向,当箭头朝下时dbu=1,反之dbu=-1;同理,当箭头朝左时dlr=1,反之dlr=-1。在垂直和水平方向的层次间网格跨度lsp分别使用rbu和rlr表示,其在顶点着色器上通过拟合函数控制规则网格中的顶点位置的算法如算法1所示。其中函数f即为各种曲线控制函数,通过修改函数f的形式,可以得到不同的裂缝修补方式。
算法1 拟合函数控制规则网格中顶点位置
输入:顶点初始位置orgvertex,顶点间距fstep,
箭头方向参数rlr,rbu,
层次跨度参数dlr,dbu,
网格块左下角位置vleftdown,网格块大小blocksize。
输出:顶点偏移后位置realvertex。
1 垂直方向上顶点到Y轴的跨度Mv=(int(orgvertex)%rbu)/2;
2 If dbu==1
3 realvertex.x=(orgvertex.x-Mv)+
Mv.f(orgvertex.y);
4 Else
5 realvertex.x=(orgvertex.x-Mv)+
Mv.f(blocksize-1-orgvertex.y);
6 水平方向上顶点到X轴的跨度Mh=(int(orgvertex)%rlr)/2;
7 If dlr==1
8 realvertex.y=(orgvertex.y- Mh)+
Mh.f(orgvertex.x);
9 Else
10 realvertex.y=(orgvertex.y-Mh)+
Mh.f(blocksize-1-orgvertex.x);
11 输出偏移后顶点位置realvertex=vleftdown+realvertex*fstep;
基于瓦块四叉树的Chunked LOD模型,将大规模高程数据分割成块,并使用四叉树结构层次化管理,该模型能够通过精确的误差测度来最小化绘制规模,减少CPU-GPU间的数据调度,是目前应用最广泛的大规模规则网格数据实时可视化策略。但其节点层次的多样性带来了裂缝修补的不确定性,常用的垂直裙边方式可以通过设定垂直三角形来掩盖几何块间的裂缝,却并没有从根本上解决几何块间网格不连续的问题,只能应用于对网格质量要求不是很高的情形。
为实现曲线函数拟合方法在Chunked LOD中的应用,在主存中通过下采样并层次化剖分规则网格来构建瓦块四叉树。与Ulrich[ 1]和Dick[ 17]的思想相似,通过几何空间误差测度进行层次细节选择和可见性裁剪获得需要渲染的网格块。在预处理阶段,通过式(2)计算网格块的几何空间误差。
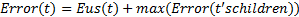 | (2) |
式中:Eus(t)表示通过上采样获取的网格块 t自身的最大几何偏差。
在构建瓦块四叉树阶段,获取网格块包围体和邻居信息用于四叉树LOD选择。绘制时使用队列来存储需要绘制的网格块节点,整个可视化过程分为LOD选择和渲染两个阶段。LOD选择阶段:遍历整个四叉树,选择需要绘制的节点添加到绘制队列中;绘制阶段:计算控制网格块偏移的参数值 
本文实验使用的计算机配置为Intel Xeon E5482 3.2 GHz处理器,4 G内存,Nvidia Geforce GTX460显卡。经过实验,将本文提出的利用参数化拟合函数解决裂缝的方法与目前主要的几种裂缝处理方法在性能上进行了对比分析,并对文中四种曲线函数拟合网格的质量进行了对比分析。
表1是裂缝修补性能对比结果,曲线拟合方法能够直接在绘制时执行,无须裂缝预处理,且只需规则网格块一种几何绘制类型。相比之下,Clipmaps[ 3]和Chunked LOD[ 1]在预处理阶段需要生成弥补块间裂缝的“裙边”三角形条带;Seamless Patches[ 13]在预处理阶段除了生成基础网格块,还需要生成弥补块间裂缝的过渡网格块;GeoMipMaps[ 4]则需要在绘制之前根据块相邻关系动态地删除顶点来调整网格布局。RASTeR[ 10]只使用三角形块作为绘制类型,但三角形块层次间约束关系使其很难支持多跨度LOD裂缝处理。CDLOD模型[ 18]支持基于GPU的裂缝处理,但平缓LOD过渡的思想会引入很多尖锐的狭长三角形,导致绘制质量不理想,而通过调整曲线形状,参数化曲线函数拟合方法能够有效地避免狭长三角形的产生。
| 表1 不同裂缝消除方法的性能指标比较 Table 1 Comparison among different repairing cracks method |
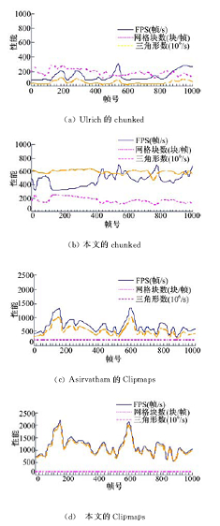
在基于GPU裂缝处理的LOD实时可视化架构上,使用Puget Sound地形规则网格数据作为测试数据,数据规模为4000×4000,采样精度40 m,绘制窗口大小为1920×1080,实现了基于GPU裂缝处理的Chunked LOD和Clipmaps两种多尺度LOD架构的漫游实验测试。在整个漫游过程中随机抽取1000帧对使用参数化裂缝消除与原有裂缝修补方法的绘制性能进行了对比。
对于Chunked LOD模型,可视化测度取屏幕空间误差阈值2个像素,细节层次采用7层,规则网格块规模为33×33。图6(a)和图6(b)是使用传统”裙边”与参数化曲线函数解决裂缝方法的帧率、绘制吞吐量以及绘制块规模的对比曲线。使用参数化曲线函数方法,CPU在整个绘制阶段中只需执行LOD选择,其他均在GPU上完成,充分发挥了GPU并行加速性能,每秒渲染三角形数量能够达到590×106,平均帧率为474 帧/s,最低帧率为312 帧/s。
对于Clipmaps模型,取网格块大小为65×65,采用纹理循环形式扩展可视化范围,嵌套层次取10层。对比曲线如图6(c)和图6(d)所示,参数化解决裂缝的Clipmaps有效减少了绘制网格的块数,加速了并行绘制的性能,较Asirvatham的Clipmaps方法[ 3]在帧率和面片吞吐量上都有一定程度的提升。
分别对分段、线性(Strugara[ 18])和反正切函数裂缝修补效果进行了对比分析。图7展现了规则网格石雕LOD模型应
 | 图7 不同曲线函数顶点偏移区域(彩色区域)面积对比Fig.7 Colorful regions represent result of vertices morphing after repairing cracks by different functions |
用各种曲线函数修补裂缝后,狭长三角形在模型表面的分布效果。图中彩色区域代表由于修补裂缝引起的狭长三角形区域,可以看出,线性函数顶点偏移覆盖区域分布在整个网格块中,而分段函数和反正切函数则只分布在裂缝出现的块边界地带,纹路与未处理前基本相同,比Strugara方法[ 18]更好地保证了网格块内部可视化质量。图8和图9分别是使用本文的反正切函数弥补裂缝方法最终生成的多尺度地形和浮雕实时可视化效果图。
提出了一种新的解决多尺度规则网格LOD模型裂缝处理策略——参数化曲线函数拟合方法。通过引入一系列的数学曲线函数控制T型顶点规则地偏移,解决了多分辨率网格平滑过渡的问题,并设计实现了该方法的GPU加速功能,取得了高的绘制速度和质量。由于曲线函数拟合参数化方法具有简单、高效、易用以及灵活的特性,因此能够很容易地应用在目前许多规则网格LOD模型中。在大规模、高精度的三维模型可视化需求的驱动下,OpenGL4.0和Directed3D 11均引入了基于GPU的网格细化技术-Tessellation着色器。目前,Tessellation着色器在构建高精度网格模型中已经展现了强大的处理功能,但是还没有很好地解决Patch间网格连续性问题。作者发现参数化处理裂缝方法同样适用于Tessellation着色器改善网格连续性,因此下一步将在硬件Tessellation多尺度实时绘制方面进行更深入的研究。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|