近年来,各国学者对立体匹配方法进行了深入的研究,如Scharstein等^{[ 1]}提出可按照4个主要步骤来实现立体匹配,即匹配代价的计算、匹配代价的叠加、视差计算与优化、视差细化。Tombari等^{[ 2]}对基于局部或全局匹配代价的叠加方法作了进一步的归类和比较。葛亮等^{[ 3]}提出以纹理单一区域代替像素来获取视差图;该算法计算时间短,在低纹理区域能有效降低误匹配率。Klaus等^{[ 4]}在图像分割基础上融入了置信度传播^{[ 5, 6]}和自适应非相似测度算法,在一定程度上减少了“块效应”,保留了细节成分,但算法计算复杂,花费时间较长。Zitnick等^{[ 7]}采用过分割的方法,通过将分割区域细化,在高纹理区域取得了相对准确的视差图,但在低纹理区域仍然会存在较大的误差。Papadakis等^{[ 8]}采用图像分割优化和多重标记细化算法,提高了视差图的精度。De-Maeztu等^{[ 9]}在局部匹配算法中采用基于梯度的相似匹配方法,提高了算法对图像像素畸变、噪声的鲁棒性。此外,文献^{[ 10, 11]}分别将协同优化算法和能量最小化方法应用到立体匹配算法中,也都取得了不错的效果。除此之外,文献^{[ 12]}提出了基于方向梯度直方图的自适应窗口匹配算法,可根据图像纹理大小采用不同的像素窗口,提高了算法的自适应性。

以上方法较好地解决了图像高纹理区域的误匹配问题,但由于局部匹配算法严格受限于图像的成像质量,因此在低纹理区域容易产生误匹配;除此之外,如何对遮挡区域视差信息进行有效填充也是上述算法所面临的主要问题。为此,本文拟从改进局部匹配方法入手,将其与全局匹配相结合来获取初始视差图;同时利用曲面拟合以及新的区域合并准则,力图解决上述问题。

传统的基于图像分割的立体匹配算法^{[ 12]}是图像立体匹配领域的经典算法,能够有效解决高纹理区域误匹配问题,被广泛采用,该算法大致可以分为3个主要步骤:

(1)将参考图像分割成多个颜色相近的区域;目前大多采用均值漂移算法^{[ 13]},即沿着平均梯度方向找出相似颜色收敛点,并根据收敛点之间颜色的相似性进行图像分割。

(2)利用局部匹配或全局匹配算法获得初始视差图。

利用局部匹配方法能够快速得到初始视差图,基于窗口的局部匹配算法定义为

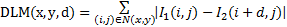(1)

式中:N(x,y)表示目标像素点周围窗口的大小,即图像中所有像素的四邻域点集;I₁、I₂分别表示左、右图像像素点值。

与局部匹配算法相比,基于全局的匹配算法主要是在匹配代价的基础上增加了平滑性约束,同时将对应点的局部匹配问题转化为全局视差分布的最优解问题,其定义为

(2)

式中:d表示整幅图像的视差分配;d_p表示p点所分配的视差值;平滑项V(d_p,d_q)表示两相邻像素点p、q点分配视差d_p和d_q时的视差不连续惩罚量;P(x,y)表示图像中像素点的集合,数据项D_p(d_p)表示p点视差为d_p时非相似性测度。

(3)利用平面拟合方法对各个分割区域内的像素点进行拟合,获得视差平面集;然后利用各种优化方法,如贪婪优化算法、图切割优化算法^{[ 8]}对视差平面集进行优化。

传统的基于图像分割的立体匹配算法是采用基于窗口的局域匹配方法来获得初始视差图,对纹理图像的鲁棒性较低,除此之外,传统方法是利用平面拟合方法对各个分割区域进行处理,在分割区域交界处往往会产生较大误差,极易产生“块效应”。

本文方法是首先对传统截断绝对差值方法(TAD)^{[ 6]}作了改进,并将其与置信度传播方法(BP)^{[ 9]}相结合,以获得原始视差图;然后通过对左、右视差图进行一致性检测,提取出有效的像素点集,提高视差图的准确性;最后采用曲面拟合的方法对各个分割区域进行处理,并利用新的合并原则对相邻分割区域进行合并,以提高各区域之间的平滑性。

2.1 视差估计

目前广泛采用的匹配方法是利用像素点值和一个聚合窗口来对左、右图像进行匹配,该方法虽然能够较好地修复图像中的一些畸变点,但同时也会丢失部分细节信息;而全局匹配虽然能够保证图像细节不丢失,但对畸变点不具有修复功能,在畸变点处容易产生误匹配。为此,本文对传统截断绝对差值(STAD)局部匹配算法进行了改进,并将其与基于置信度传播(BP)全局算法相结合,以克服两种方法各自的缺点,实现对图像视差的预估计。

本文利用梯度信息对STAD方法进行改进。传统算法所采取的单一方向梯度容易受到像素畸变、噪声等因素的影响,不能准确地反映出图像的纹理特征,为此,本文拟同时考虑4个方向梯度,使参考图像与目标图像像素点匹配对应,以消除图像中单一像素点畸变所带来的误匹配,提高算法的鲁棒性。

基于梯度的非相似测度方法定义为

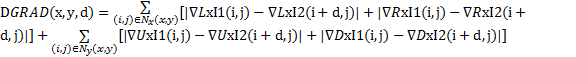(3)

式中:N_x(x,y)表示不包含最左、最右列图像点集;N_y(x,y)表示不包含最上、最下行图像点集;∇ _Lx、∇ _Rx、∇ _Ux、∇ _Dx分别表示从左到右、从右到左、从上到下、从下到上的梯度。

给定一个最优权重ω,令:

D _TG(x,y,d)=D _STAD(x,y,d)+ωD _GRAD(x,y,d) (4)

定义置信度能量函数E _BP,其与匹配代价函数D _TG的关系可以表示为

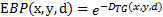(5)

本文采用消息更新机制来实现置信函数的最大化,匹配代价最小化问题可以转化为能量函数最大化问题来处理,消息迭代传输可以定义为

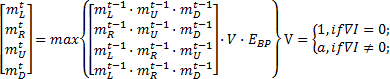(6)

式中: 、 、 、 分别表示为像素点左、右、上、下传递的信息;t表示迭代的次数;V为平滑项;∇I为图像梯度;迭代完成后,即可求出稠密视差图:

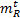
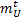
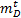
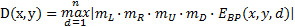(7)

式中:n为视差最大值。

通过对左、右视差图进行一致性校验,可以将初始匹配中的错误视差值剔除,其表达式为

D _L(x _L)=D _R(x _L-D _L(x _L)) (8)

式中:D _L、D _R分别表示左、右视差图。

对于所有像素点,如果满足式(8),则认为该像素点为可靠匹配点,反之则认为是误匹配点。通过有效像素点数与分割区域总像素点数的比值为该分割区域内有效像素点的准确率 m,可以将准确率高的分割区域定义为可靠区域。

2.3 区域合并

由于曲面拟合是在各个分割区域内分别进行的,没有从全局进行考虑,因此可能会导致各分割区域之间的不平滑。为解决这一问题,本文提出了一种新的区域合并准则,以对各个分割区域进行合并。具体作法是:首先,计算出两个相邻分割区域的曲面模型:

(10)

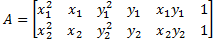
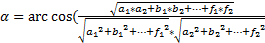
式中: a₁, a₂, b₁, b₂,…, f₁, f₂分别代表两个曲面的相关参数; ; d( x₁, y₁)和 d( x₂, y₂)表示两个相邻分割区域的深度;定义参数 α:

) (11)

如果 α小于某个给定的阈值,则认为这两个区域具有相似的曲面参数,可以合并为一个区域,并重新计算曲面拟合参数;重复上述步骤,直到所有分割区域都不能合并为止,得到最后的稠密视差图。

本文实验所用测试图均来自美国 Middlebury大学计算机视觉研究中心提供的立体图像数据库: http: //vision.middlebury.edu/stereo。这些测试图涵盖了缺少纹理区域、不连续区域、遮挡区域等各种情况,如图1 ~图3所示。3个实验中的参数设置分别为: a=4、 m=0 .8、 T=20, n分别设置为20、20、60, α分别设置为1 .35、1 .45、1 .50。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 Tsukuba视差图效果比较Fig.1 Comparison of Tsukuba disparity maps

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 Venusa视差图效果比较Fig.2 Comparison of Venusa disparity maps

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 Teddy视差图效果比较Fig.3 Comparison of Teddy disparity maps

从图1中可以看出,与传统的立体匹配相比,本文方法能够有效地减少低纹理区域的“块效应”,获得的视差值图更加准确(如墙壁、书架区域);同时也可以看出,由于采取了曲面拟合的方法,在遮挡区域(如灯的边缘)也获得了较好的匹配效果,有效地减少了视差边缘的“膨胀”效应。从图2中可以看出,传统的立体匹配算法在视差连续区域容易产生不连续的现象(如图2( b)中产生了“波纹”状视差图),而本文利用分割区域合并准则,合并了相邻的视差区域,获得的视差图更加平滑自然,特别是在距离较远的背景区域效果更加明显。同样,从图3中也可看出,本文方法在低纹理区域(如画布、屋顶部分)的误匹配明显减少,获得的视差图像更加平滑,也更符合实际场景的真实特征。

为了验证不同曲面模型的数据拟合效果,本文选取了图1 ~图3的部分区域,即图1( a)、2( a)、3( a)中白色框图区域,分别利用平面模型,以及2 ~6次曲面模型进行数据拟合,其拟合误差如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 不同平(曲)面模型拟合误差对比图Fig.4 Fitting error comparison with different planar(surface)models

由图4可看出,对于3幅标准图像,利用曲面模型函数进行数据拟合,其均方误差都要明显低于平面模型函数,而采用2 ~6次函数曲面模型,拟合误差相差不大,因此,选取最简单的2次函数进行曲面拟合,切实可行。

本文算法与传统立体匹配算法匹配结果对比如表1所示。其中, Nonocc代表非遮挡区域的误匹配率, All代表总误匹配率, Disc代表视差边缘的误匹配率,误差阈值取值0 .5。从表1可以出,无论是在非遮挡区域还是视差边缘,本文算法看的误匹配率都明显低于传统立体匹配算法,特别是“Teddy”图像,由于图像中物品多,形状不规则,而且遮挡严重,本文算法的视差边缘误匹配率明显低于传统立体匹配算法。

表1

Table 1

表1(Table 1)

表1 两种算法的误匹配率比较 Table 1 Comparison of error rate of two different algorithms % 算法 Tsukuba Venus Teddy Nonocc All Disc Nonocc All Disc Nonocc All Disc 传统算法 22.9 23.5 19.7 7.35 7.82 12.1 9.94 15.9 22.1 本文算法 15.6 16.3 17.0 5.02 6.10 8.84 7.74 9.66 15.8

表1 两种算法的误匹配率比较 Table 1 Comparison of error rate of two different algorithms %

对传统的基于分割立体匹配算法进行了改进,将改进后的局部匹配算法与基于置信度传播(BP)的全局算法相结合,改善了初始视差图的估计效果,减少了误匹配;同时利用曲面模型对初始视差图进行拟合,并在区域合并中提出了新的判断准则,获得了更加平滑的视差图。仿真实验结果表明,本文算法在低纹理和视差连续区域都能获得更准确的视差图,在遮挡区域也取得了比较理想的效果。