高印寒(1951),男,教授,博士生导师.研究方向:车辆测试技术及机器视觉.E-mail:yinhan@jlu.edu.cn
为了提升多源图像融合精度,提出了一种基于图像质量评价参数的非下采样剪切波(NSST)域图像自适应融合方法。利用非下采样剪切波变换对源图像进行多尺度、多方向分解,低频子带图像采用结构相似度与空间频率两种图像评价参数作为系数权值,高频子带图像应用绝对值与邻域平均能量一致性选择的融合策略。应用非下采样剪切波逆变换重构图像。采用多组多源图像进行融合实验,并对融合结果进行了客观评价。实验结果表明:本文方法在主观和客观评价上均优于其他多尺度融合方法,具有更好的融合效果。
To enhance the multi-source image fusion accuracy, an adaptive fusion method based on image quality assessment parameter in Nonsubsampled Shearlet Transform (NSST) domain is proposed. The Source images are decomposed to subband images with multi-scale and multi-direction in NSST. The low frequency subband fusion rule is based on the structural similarity index with spatial frequency as coefficient weights. For the high frequency subands, the fusion rule of coefficient absolute value with neighborhood average energy consistency selection is adopted. The fused low and high frequency coefficients are reconstructed to image by nonsubsampled shearlet inverse transform. Fusion experiments are conducted with several sets of different modality images, and the objective assessment of fused results is done. The experiment results show that the proposed algorithm performs better in subjective and objective assessments than a few existing multi-scale fusion techniques, and obtains better fusion performance.
目前,图像融合多数都采用基于多尺度分解的融合方法,其融合效果要优于单尺度融合方法[ 1]。多尺度融合方法要解决两个核心问题:①采用何种多尺度分解方法分解源图像;②采用何种融合策略融合分解后的子带图像。
对于第一个问题,离散小波变换(DWT)所具有的空频域分析图像能力在图像融合领域得到广泛应用[ 2, 3]。小波变换在分析点状瞬态特征的奇异性时是最优基,但不能“最优”地表示图像结构中的直线或曲线的奇异性。为了解决小波变换的局限性,先后提出了Curvelet变换[ 4]和Contourlet变换[ 5],这两种变换具有很好的方向敏感性和各向异性,能够准确地捕获图像中的边缘信息,取得了良好的融合效果。但这两种多尺度分解方法与二维离散小波变换一样,缺乏平移不变性,在融合结果中容易引入伪Gibbs效应。文献[ 6]提出了一种新颖的多尺度几何分析工具——非下采样剪切波变换(NSST),它不仅具有Curvelet和Contourlet变换的优点,同时具有平移不变性。本文对图像多尺度几何分解方法采用非下采样剪切波变换。
对于第二个问题,传统的融合策略多采用对低频子带图像进行简单等权值的加权平均,高频子带图像直接选取最大系数(像素)进行融合。这种融合策略不能根据图像的具体信息特征分配权值,削弱了图像的对比度,不具有自适应性,在图像含有噪声时,导致融合后的图像具有一定的不连续性和不稳定性。文献[7]对传统融合策略中低频融合规则进行了改进,采用区域能量取大的规则选取系数,一定程度上提高了融合图像的对比度,但仍对图像中噪声比较敏感。文献[ 8]提出一种将主成分分析法(PCA)用于低频子带图像的融合。通过PCA方法找到低频图像的主成分,确定待融合低频子带图像的权值。高频子带图像采用“一致性检验”融合策略来弱化图像的不连续性。PCA融合策略对各个像素点施加相同的权值,无法突出特定目标信息。文献[ 9]提出低频子带图像采用邻域方差加权平均与选择相结合的方法,高频子带采用“区域能量取大”融合策略。先计算待融合低频子带邻域窗口的方差值,根据方差值比较的结果决定采用加权平均还是像素选择融合策略,但是,对于不同类型的源图像,方差比较阈值的选取对融合结果有较大影响,自适应性较差。
本文提出了一种新的高频子带和低频子带融合算法。低频子带中,应用结构相似度与空间频率两种图像评价参数作为像素点的权值,突出目标信息;高频子带中,应用系数绝对值与邻域平均能量一致性选取像素值,消除可能出现的图像不连续性和去除椒盐噪声,使融合后的图像更符合人的视觉。
Guo等[ 10]通过经典仿射系统理论把几何与多分辨分析结合起来提出了合成小波理论,当维数n=2时,具有合成膨胀的仿射系统形式如下:
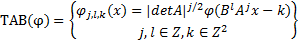 | (1) |
式中:φ∈L2(R2); A、 B为2 ×2可逆矩阵,且 |det B |=1,当T AB(φ)满足Parseval框架(也称紧框架),即对任意的f∈L2(R2)有:
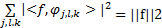 | (2) |
则称这个系统的元素为合成小波。其中,矩阵 A j是与尺度变换相关联的膨胀矩阵, B l是与面积保持不变的几何变换相关联的矩阵,如旋转和剪切变换。合成小波具有多分辨分析的属性,可以像小波一样,构造在各种尺度、位置和各个方向上的基元素的 Parseval框架。当 A为各向异性膨胀矩阵, 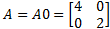

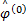
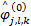
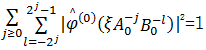 | (3) |
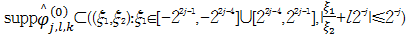 | (4) |
式中: 


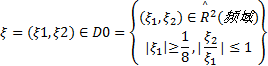
,函数{ 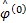
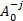
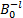
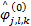
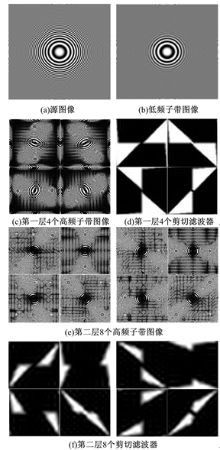
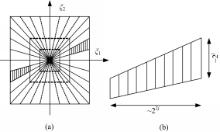 | 图1 剪切波频域剖分图以及剪切波元素频率支撑图Fig.1 Tiling of frequency plane induced by shearlets and frequency support of shearlet elements |
剪切波水平锥面元素为
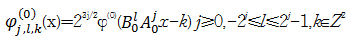 | (5) |
令 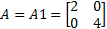
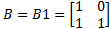
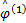

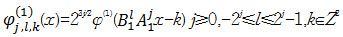 | (6) |
形成一个 D1剖分,如图1( a)中虚线部分。剪切波是一种接近最优的图像稀疏表示。
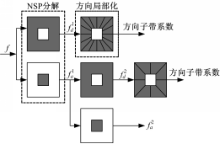
非下采样剪切波变换过程主要分两步:非下采样金字塔( NSP)分解和方向局部化。前者采用二通道非下采样滤波器组使 NSST具备了多尺度性,源图像经一级 NSP分解可产生一个低通子带图像和一个带通子带图像,以后每一级 NSP分解都在低通分量上迭代进行,以获取图像中的奇异点。因此,二维图像经 k级 NSP分解后,可得到 k+1个与源图像具有相同尺寸的子带图像,其中包括1个低通图像和 k个大小相同但尺度不同的带通图像。方向局部化是通过剪切滤波器( SF)实现的。从伪极化坐标映射到笛卡尔坐标,应用 Meyer小波构造窗口函数,得到剪切波滤波器,将分解后的带通子带图像与 Meyer窗口函数进行二维卷积运算,得到方向子带图像。
非下采样剪切波变换过程中不存在下采样操作,使其具备了平移不变性。其过程如图2所示, NSST具有非常好的局部化特性,非常高的方向敏感性,满足抛物线尺度化特性。
图像f经过k层NSST分解,会得到 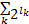
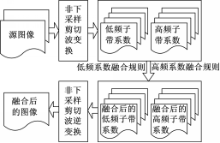
多尺度图像融合包括多尺度分解、子带融合和图像重构三个过程。待融合图像分别进行非下采样剪切波分解,得到高频和低频子带图像,对低频和各层高频子带图像应用不同融合策略分别进行融合,最后应用非下采样剪切波逆变换重构,得到融合图像。具体过程如图4所示。
图像的低频分量集中了图像的主要能量,反映图像的近似和平均特性,高频子带图像反映的是图像的细节,如直线、轮廓等信息。为了能够准确地提取待融合图像中的最优部分,满足人类视觉系统的要求,本文在低频子带融合策略中引入图像质量评价准则,在融合前对图像片区域的质量加以评判。高频子带融合采用单点信息与区域信息结合的算法选取该位置的像素。设源图像I1和I2经过NSST分解后得到不同尺度、不同方向的子带系数分别表示为 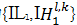
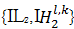
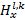
2.2.1 低频子带图像融合策略
图像信号是高度结构化的,像素间具有很强的相关性,这些相关性携带了场景中物体结构的重要信息。人眼视觉的主要功能是提取背景中的结构信息,而视觉系统能够高度自适应地实现这一功能,因此对图像结构信息的改变量进行度量是图像感知质量的最好近似。文献[ 12]将图像间局部亮度、对比度和结构信息归一化到一个量对两幅图像的结构相似度进行评价。图像x和y,区域窗口中心点(i,j)的局域亮度、对比度和结构信息分别定义如下:
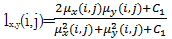 | (7) |
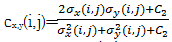 | (8) |
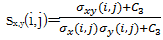 | (9) |
式中:μx、μy、σx、σy和σxy分别为图像x和y的局域窗口均值、标准差和协方差;Ci(i=1,2,3)是为了避免式中分母为零而引进的常数,在具体应用时,取C1=C2=2C3。
局域窗口取标准差为1.5的高斯窗口。结构相似图像评价指标定义如下:
SSIMx,y(i,j)=lx,y(i,j)·cx,y(i,j)·sx,y(i,j) (10)
文献[ 13]提出的空间频率图像评价指标反映了一幅图像本身的总体活跃程度,空间频率越大图像越活跃、越清晰,对于一个M×N的图像块,设在位置(i,j)处的灰度值为f(i,j),则空间频率定义为
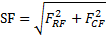 | (11) |
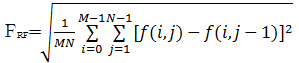 | (12) |
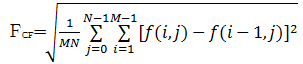 | (13) |
式(12)称为水平方向频率,式(13)称为垂直方向频率。
低频子带融合策略的目的是在融合结果中根据源图像的局部特征尽量保持局部亮度、对比度和清晰度。在已有的加权平均融合方法中,权重都是直接与源图像的局部或全局显著特征相关的值,融合过程容易受到噪声的干扰,在融合结果中容易引进虚假信息,得不到合适的局部亮度和结构信息。
源图像中,局域活跃程度越高,图像越清晰,表明像素在融合中所占的权重越大。如果融合后的图像已知,融合图像与源图像的结构信息越相似,表明源图像中所对应像素的权值越大。本文设计了一种根据图像自身局域活跃程度和融合后局域结构相似度两种图像评价参数决定像素权值的低频融合策略。具体步骤如下:
(1)低频子带均值加权融合
在低频子带中,采用等权值的加权平均,获取初始融合的估计图像,这种方法虽然平均了原图像的亮度与对比度,但可作为结构相似度度量的参考图像,以便获取最佳权值。
ILF=(IL1+IL2)/2 (14)
(2)计算局域结构相似度参数
在系数矩阵ILF、IL1和IL2中选择以点(i,j)为中心的局域窗口N×N,根据式(10)计算局域结构相似度,得到 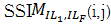
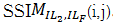
(3)计算局域窗口结构相似度参数归一化系数
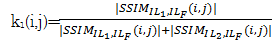 | (15) |
k2(i,j)=1-k1(i,j) (16)
通过计算源图像与初始融合图像窗口中心点的结构相似度值,反映图像间局部结构相似程度,用结构相似度值作为中心系数的权值,可以保留源图像的亮度与对比度。
(4)计算局域窗口空间频率
在系数矩阵IL1、IL2中,根据式(11)计算局域窗口N×N中点(i,j)的空间频率,得到S 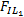

(5)计算局域窗口空间频率归一化系数
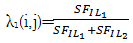 | (17) |
λ2(i,j)=1-λ1(i,j) (18)
空间频率表示图像的梯度特征,空间频率越大表明图像越活跃,结构细节越清晰,用空间频率作为系数的权重,可保留源图像中细节信息。
(6)计算低频子带系数权重
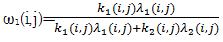 | (19) |
ω2(i,j)=1-ω1(i,j) (20)
应用源图像与初始估计融合图像的局域窗口结构相似度作为权重值可保留待融合图像中的亮度与对比度,应用图像自身的空间频率特征作为权重可保留源图像的细节信息,通过“与”的关系将二者信息整合,就可以由ω1、ω2确定待融合图像对当前像素点应有的贡献。
(7)计算低频子带融合系数
ILF(i,j)=ω1(i,j)·IL1(i,j)+ω2(i,j)·IL2(i,j) (21)
上述步骤(2)~(7)遍历整个低频子带系数矩阵,得到低频子带系数 IL。
2.2.2 高频子带图像融合策略
高频子带融合的目标是提取源图像中的边缘结构,在已有的高频子带图像融合策略中,多采用直接选取绝对值最大系数(像素)或局部区域能量取大原则进行融合。直接选取绝对值最大系数(像素)可以获取高频子带图像中丰富的边缘信息,但这种融合策略只考虑了像素的单点信息,容易造成图像的不连续性,且不能很好地去除椒盐噪声。局部区域平均能量取大融合策略由于考虑了区域内各像素之间的相关性,降低了对噪声的敏感性,但这种融合策略容易使图像轮廓与非轮廓区域之间模糊,造成融合图像清晰度降低。因此,本文整合上述两种融合策略的优点,提出了一种系数绝对值与邻域平均能量一致性选择的融合策略,以达到在降低对噪声敏感性的同时,最大限度地提取源图像中边缘细节和亮度信息,提高融合图像的清晰度。其基本思想是在区域窗口M×M中,采用系数绝对值与邻域平均能量一致取大的原则选取区域中心像素点。具体融合步骤如下:
(1)计算区域窗口平均能量
在高频子带系数矩阵I 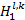
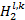
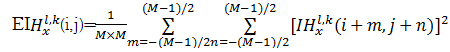 | (22) |
式中:x值为1或2。
(2)融合系数选择
根据区域窗口的平均能量值和中心系数绝对值选取融合系数:
①在 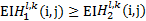
如果 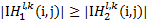
 | (23) |
否则,即|I 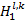
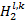
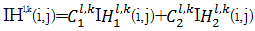 | (24) |
②在 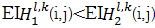
如果 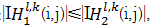
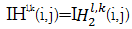 | (25) |
否则,即 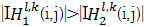
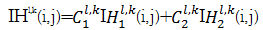 | (26) |
式中: 
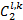
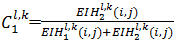 | (27) |
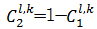 | (28) |
上述过程遍历整个高频子带系数矩阵,得到高频子带融合系数IHl,k。
评价图像融合效果的方法分为主观评价和客观评价两种方法。主观评价方法是评价人员直接对图像进行评估,简单且直观。对于有明显信息变化的融合图像可快捷、方便地做出主观评价。客观评价方法是对融合后的图像计算其均方根误差、交叉熵、信息熵、交互信息量和边缘信息传递量等指标来衡量融合效果。由于没有参考图像,本文对于融合效果的客观评价采用信息熵(EN)[ 14]、交互信息量(MI)[ 15]和边缘信息传递量( Q AB/F)[ 16]。
(1)信息熵(EN)
设图像总的灰度级数为L,则图像的信息熵定义为
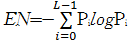 | (29) |
式中:Pi表示灰度值为i的像素数Ni与总的像素数N之比,即
Pi=Ni/N (30)
图像的信息熵越大,表示融合图像所包含的信息越丰富,融合质量越好。
(2)交互信息量(MI)
设源图像分别为A和B,融合图像为F,灰度值范围分别为[0 a]、[0 b]和[0 f],F与图像A、B的交互信息量定义为
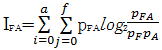 | (31) |
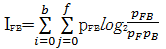 | (32) |
式中:pA、pB和pF分别为图像A、B和融合图像F的概率密度;pFA和pFB分别表示两组图像的联合概率密度,综合考虑式(31)(32),融合图像F包含源图像A、B的交互信息量定义为
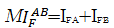 | (33) |
MI值越大表示融合图像从源图像中获取信息的丰富程度越高,融合效果越好。
(3)边缘信息传递量(QAB/F)
设源图像分别为A和B,融合图像为F,边缘信息传递量定义如下:
Q(i,j)=QAF(i,j)ωA(i,j)+QBF(i,j)ωB(i,j) (34)
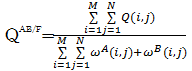 | (35) |
式中:ωA(i,j)、ωB(i,j)为权重;QAF(i,j)和QBF(i,j)定义见文献[ 16]。
QAB/F值越大,说明融合图像保留源图像中边缘信息越多,融合效果越好。
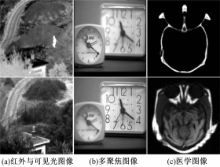
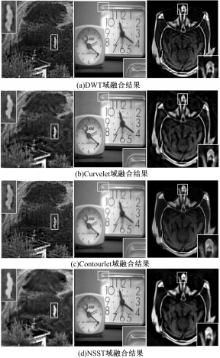
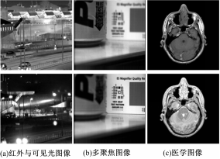
为了验证非下采样剪切波变换的多方向性和平移不变性在图像融合领域的优越性,采用传统融合策略在NSST域、DWT域、Curvelet和Contourlet变换域对图5所示红外与可见光、多聚焦和医学3组不同模态的图像进行融合实验,并对结果进行客观评价。
从图6融合结果及放大图像中可以看到,在红外与可见光图像中目标周围出现不同程度的伪影现象,而图6(d)图像清晰自然。这是由于DWT、Curvelet和Contourlet变换缺乏平移不变性引起的伪吉布斯效应。图6的融合结果表明:在光谱差异较大的源图像融合过程中,NSST所具有的平移不变性能够有效地克服伪吉布斯效应。图6(b)(c)(d)中时钟边缘的刻画要优于图6(a),表明Curvelet、Contourlet和NSST所具有的多方向性和各向异性对图像边缘的刻画会更细致。图6(d)中骨骼边缘及软组织的提取要优于图6(a)(b)(c),这表明NSST所具有的局部化特性、高方向敏感性和抛物线尺度化特性在图像细节的提取方面具有一定的优势。应用图像客观评价指标信息熵(EN)、交互信息量(MI)和边缘信息传递量(QAB/F)对融合图像进行客观评价,评价指标列于表1中。从表1的数据可看到,应用NSST融合的图像客观评价指标均为最优,这也说明在图像融合领域,NSST要比DWT、Curvelet变换和Contourlet变换更具有优势。这也是本文选用NSST作为多尺度分解工具的原因。
| 表1 不同多尺度分解方法融合结果的比较 Table 1 Fusion results comparison using different multi-scale decomposition methods |
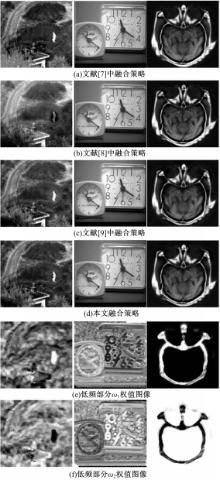
为了验证本文融合策略的有效性,在NSST域,分别应用本文融合策略、文献[ 7]融合策略、文献[ 8]融合策略和文献[ 9]融合策略对图5中的源图像进行融合实验,并对融合结果作了客观评价。
从图7中可以发现,在图7(d)中白色的人、路、栅栏和树清晰可见,对比度适中,相对于图7(a)(b)(c)有更好的视觉效果,这表明应用本文融合策略能够更好地提取目标信息。对于时针边缘和骨骼边缘图像,本文融合策略融合结果与文献[7][8][ 9]的融合结果视觉上差异并不大,但仔细观察,在图7(d)的时钟边缘图像中,本文融合策略融合图像更清晰,边缘刻画更准确。这表明本文的融合策略能够更好地提取边缘信息。在图7(d)中,本文融合策略融合图像中骨骼和软组织结构细节信息更系统和详实。这表明本文融合策略能够最大程度地提取源图像中的结构细节信息。图7(e)与图7(f)中的权值图像也表明了本文低频融合策略中权值的有效性。
对图7分析可知,利用本文融合策略融合的图像更能体现源图像的细节信息,保证了图像的整体清晰度,并保留了源图像中的结构信息。这是由于在低频子带图像中,应用结构相似度与空间频率两种图像评价参数作为像素点的权值,增强了融合图像的对比度,突出了目标信息。在高频子带中,应用系数绝对值与邻域平均能量一致性指导该位置像素的选取,保留了边缘细节丰富区域,消除可能出现的图像不连续性和去除椒盐噪声,使融合后的图像更符合人的视觉。客观评价指标列于表2中。从表2中可以看出,在NSST域下,本文提出的融合策略融合的图像质量评价参数为最优,进一步验证了本文融合策略的有效性。
| 表2 不同融合策略融合结果的比较 Table 2 Fusion results comparison using different fusion rules |
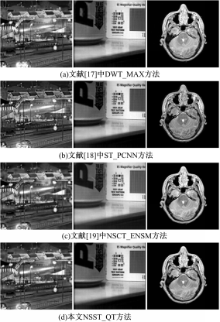
将本文融合方法NSST_QT与文献[17]中DWT_MAX方法,文献[ 18]中ST_PCNN方法,文献[ 19]中NSCT_ENSM方法进行比较, 以验证本文提出的多尺度分解方法与融合策略的有效性。源图像采用图8中红外与可见光、多聚焦和医学3组不同模态图像。融合结果如图9所示,客观评价指标如表3所示。
| 表3 不同多尺度融合方法融合结果的比较 Table 3 Fusion results comparison using different multi-scale fusion methods |
针对已有的多尺度几何分析图像融合方法的缺陷,本文将NSST引入图像融合领域,提出了基于图像质量评价参数的NSST域图像自适应融合方法。NSST所具有的抛物线尺度化特性、平移不变性、高的方向敏感性和优良的局部化特性,可有效地提取源图像的特征信息。在融合过程中,对低频子带图像采用结构相似度与空间频率两种图像评价参数作为像素点的权值;对高频子带应用系数绝对值与邻域平均能量一致性选择的融合策略。实验结果表明,本文提出的图像融合方法与其他融合方法相比较,能够得到较好的融合效果,具有较强的自适应能力。同时,本文所提出的融合策略也可应用于其他多尺度图像融合。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|