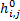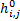零部件的粗糙表面形貌严重影响摩擦、磨损、密封、疲劳强度等结合面接触性能,为准确建立结合面接触模型,分析、预测结合面接触性能,必须首先获取零部件的粗糙表面形貌数据^{[ 1]}。获取方法主要有直接测量和数字化模拟两种方式。直接测量能够获取粗糙表面形貌最真实的数据,但测量设备价格昂贵,测量速度慢,测量结果受环境因素影响大等缺点;需要加工大量试件并进行测量,这将造成大量经费、时间的消耗。数字化模拟操作简单方便,不受测量设备、试件及测量环境限制,能根据设定的参数模拟生成各种粗糙表面以满足结合面接触性能研究的需要。国内外学者在粗糙表面数字化模拟方面开展了大量研究,Uchidate等^{[ 2]}采用无关联自回归模型模拟三维粗糙表面;Wu^{[ 3]}、Reizer等^{[ 4]}通过快速傅里叶变换模拟粗糙表面;陈辉^{[ 5]}、田爱玲等^{[ 6]}利用FIR滤波器进行粗糙表面形貌的模拟。这些方法在模拟相关长度较小的粗糙表面中效果较好,当自相关长度较大时,模拟效果不够理想。

通过矩阵线性变换模拟粗糙表面最早由Patir^{[ 7]}提出,在具有不同自相关长度的粗糙表面模拟中取得了较好的效果;但存在存储空间大、无法收敛等问题,故并未被广泛采用。为此,Bakolas^{[ 8]}、Manesh^{[ 9]}等采用非线性共轭梯度法对非线性方程组进行求解,但受所采用的非线性共轭梯度法的限制,在解非线性方程组时存在收敛速度慢等缺点。

本文根据线性转换矩阵法,采用改进的非线性共轭梯度法,结合Johnson转换系统,提出了一种新的非高斯粗糙表面数字化模拟方法。

通过矩阵线性变换模拟粗糙表面,是通过转换矩阵对单位方差的高斯分布矩阵进行线性转换,生成具有自相关函数特征的粗糙表面高度分布矩阵。设(M+m)×(N+n)矩阵η_i,j是单位方差的高斯分布矩阵,m×n矩阵R_p,q是设定的自相关函数矩阵,则M×N矩阵z_i,j是生成的粗糙表面高度分布矩阵,则

(1)

式中:h_k,l为转换矩阵,则:

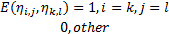(2)

由自相关函数的定义可知:

(3)

共轭梯度法适用于梯度存在的最小化函数f(x)问题。函数f(x)的最小值点也是f’(x)=0的点,本文将式(3)表达的非线性方程组改写为

(4)

为得到转换矩阵 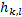,本文采用改进的非线性共轭梯度法对由式(4)构造的非线性方程组进行求解。

共轭梯度法的基本思想是把共轭性和最速下降法结合,利用已知点处的梯度构造一组共轭方向,并沿这组方向进行搜索,求出目标函数的极小点。对于无约束优化问题:min f( x)非线性共轭梯度法求解的迭代过程如下^{[ 10]}:

(5)

(6)

式中:g_k=-f'x_k为 fx在 x _k处的梯度; d _k是搜索方向; α_k是步长因子; β _k是标量参数。

非线性共轭梯度法迭代计算的关键是初始解 x₀的确定以及每步迭代中 α_k和 β _k的计算。

2.1 初始解

对于式(4)的初始解 可根据Patir^{[ 7]}的推导得到:

(7)

式中:

为便于非线性共轭梯度法计算,将 转换为一维列向量,从而得到初始解 x_0。

2.2 步长因子

步长因子 α_k的计算对非线性共轭梯度法的迭代求解过程至关重要,它是从 x _k沿搜索方向 d _k寻找一个最优点作为下一个迭代点,即在搜索方向 d _k函数值达到最小的点。因此,最佳的步长因子 α_k应满足^{[ 11]}:

(8)

步长因子 α_k难以精确计算,根据本文实际,即只有梯度函数的确定表达式,采用Secant法^{[ 10]}通过迭代求取步长因子 α_k设Secant法最大的迭代次数为 j_max,最大允许误差为ψ,则当 或迭代次数j> j_max时,Secant法迭代终止,获得步长因子 α_k。

2.3 参数

搜索方向 d _k是使得函数值局部下降的方向,其对非线性共轭梯度法的全局收敛性及收敛速度具有重要影响,由式(6)可知, d _k的计算主要是确定标量参数 β _k。 β _k的不同取法对应不同的非线性共轭梯度法,本文采用Liu等^{[ 11]}提出的一种全局收敛性较好的参数 β _k确定方法,即:

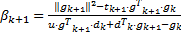(9)

式中:

2.4 迭代终止条件

设 ξ为判别迭代终止的允许误差,k_max是最大迭代次数,则当‖g_k ‖≤ ξ•‖g₀ ‖,或者迭代次数k≥k_max时,迭代终止。本文采用的非线性共轭梯度法计算流程如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 改进非线性共轭梯度法计算流程图Fig.1 Flow chart of improved non-linear conjugate gradient method

Johnson转换系统^{[ 12]}可将一个高斯分布的随机序列转变为具有一定偏斜度和峰度值的非高斯序列。针对不同的情况,Johnson转换系统所描述的系统曲线经变换包括以下3种形式:

对数正态系统(Lognormal system,SL):

无界系统(Unbounded system,SU):

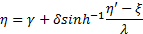
有界系统(Bounded system,SB):

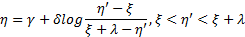
式中: η是高斯随机序列; η'是具有给定偏斜度和峰度的非高斯序列; γ、 δ、 ξ、 λ是由给定的偏斜度和峰度等参数计算得到的转换系数。

当随机序列经转换矩阵变换后,其偏斜度和峰度值将会发生改变。为了获得具有指定偏斜度和峰度的输出序列,需要对指定的偏斜度和峰度值进行修正。设输入序列的偏斜度和峰度分别为 SK _η 、 K _η,则输出序列的偏斜度和峰度为

(10)

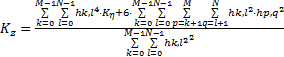(11)

本文模拟粗糙表面的具体步骤为:

(1)生成高斯序列矩阵。

(2)根据设定的自相关函数生成自相关函数矩阵,并构建计算转换矩阵的非线性方程组。

(3)通过改进的非线性共轭梯度法对非线性方程组进行迭代求解,得到转换矩阵。

(4)根据式(10)(11)对给定的偏斜度和峰度进行转换,通过Johnson转换系统将高斯序列转换为具有设定偏斜度和峰度的非高斯序列。

(5)通过转换矩阵对非高斯序列进行线性转换,得到具有设定自相关函数特性的非高斯粗糙表面。

(6)计算得到的粗糙表面峰度、偏斜度与设定值的误差,如果超过最大允许误差,则重复步骤(3)~(5)。

粗糙表面形貌具有多种自相关函数类型,在粗糙表面模拟过程中,常采用指数型自相关函数^{[ 6, 8]}:

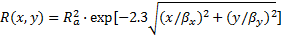
式中: 是粗糙表面的标准差; β_x、 β_y分别是x、y方向上的自相关长度。

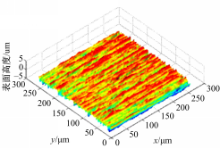
通过共聚焦显微镜对研磨加工的试件表面形貌进行测量,如图2所示,计算得到该表面的自相关长度 β _x=80 μm、 β _y=3 μm、偏斜度SK=-0.43、峰度KU=3.2。根据实测表面的相关参数,采用指数型自相关函数,运用本文方法模拟生成一个类似的粗糙表面,如图3所示。由图2、图3对比可以看出,本文方法模拟的粗糙表面与实测的试件表面形貌具有较高的相似性。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 实测研磨试件表面形貌Fig.2 Measured grinding part surface

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 本文方法模拟的粗糙表面Fig.3 Simulated rough surface by proposed method

运用本文方法模拟了一组采样间隔1 μm,偏斜度SK=0.2,峰度值KU=4的256×256非高斯粗糙表面,对模拟的粗糙表面的偏斜度、峰度进行统计,结果如表1所示。统计结果表明,本文方法模拟的非高斯粗糙表面偏斜度、峰度与设定值的误差不超过3%,能够较准确地对非高斯粗糙表面进行模拟。

表1

Table 1

表1(Table 1)

表1 模拟粗糙表面峰度、偏斜度值对比 Table 1 Skewness and kurtosis contrast of simulated rough surfaces 序号 偏斜度0.2 峰度5 模拟值 偏差/% 模拟值 偏差/% 1 0.1953 -2.33 4.9520 -0.96 2 0.1994 -0.31 4.8902 -2.19 3 0.1973 -1.37 4.9141 -1.72 4 0.2060 2.99 4.9749 -0.50 5 0.1995 -0.23 4.8749 -2.50 6 0.2006 0.29 4.9695 -0.61

表1 模拟粗糙表面峰度、偏斜度值对比 Table 1 Skewness and kurtosis contrast of simulated rough surfaces

此外,本文还结合FIR滤波法和环形自相关函数模拟了不同相关长度下的粗糙表面,并与本文方法模拟的粗糙表面自相关函数进行了对比,如图4所示。由图4可看出,FIR滤波法模拟的粗糙表面相对本文方法,自相关函数存在较大偏差,特别是在自相关长度较大时,自相关函数与理论值存在较大偏差。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 不同方法模拟粗糙表面自相关函数对比Fig.4 Autocorrelation function curves contrast of simulated rough surfaces by different methods

为满足表面工程、结合面特性等研究领域对粗糙表面数据的大量需求,本文根据线性转换矩阵法,采用改进的非线性共轭梯度法,结合Johnson转换系统,提出了一种新的三维非高斯粗糙表面数字化模拟方法。仿真结果表明,本文方法模拟的粗糙表面偏斜度、峰度误差小于3%,自相关函数模拟值与理论值拟合较好,能够根据设定的高度参数和自相关函数实现粗糙表面较准确的模拟。通过本文方法模拟的粗糙表面形貌可应用于统计性、确定性结合面解析接触模型以及有限元分析模型的构建,根据构建的接触模型可进行接触面积、接触压力分布等结合面接触特性分析,为接触刚度、接触热阻、配合精度与密封等结合面接触性能的预测提供依据。实际工件受加工因素及工作条件的影响,其表面形貌可能存在划痕、裂纹、凹坑等多种奇异特征,本文在粗糙表面形貌模拟中并未考虑,还有待于进一步深入研究。