曾文潇(1974),男,副研究员,博士.研究方向:无线传感网络,现代通信技术.E-mail:zwx@ms.xjb.ac.cn
提出分布式无线传感器网络的多分段区域检查机制,区别于传统的以零为分界的两区再加上中间区段的方法,实现以分成任意区段来判断,并且依据每区段的可信赖度调整传输给数据处理中心的信号强度的策略;在数据处理中心端采用最大后验概率(MAP) 和等增益合并(EGC)的方式来做最后判断,以期达到降低传送能量和降低错误率的目标。仿真研究结果表明:本文方法具有较好的适应性,与传统方法相比,多分段区域检查机制能较明显地降低传送错误率和网络能耗。
A multi-staging area check method for distributed wireless sensor networks is proposed. The method is different from the zero boundaries and the added middle section method. With this method, the strategy with arbitrary segments for check and adjusting the transmission according to the reliability parameter from the signal strength is achieved. To reduce the transmission energy and reduce the error rate, the methods of the maximum a posteriori (MAP) and equal gain combining (EGC) are applied in the data fusion center for final check. Simulation results show that the proposed method has better adaptability. Compared with traditional method, multi-staging area check method can significantly reduce transmission error rate and reduce the energy consumption of the network.
无线传感器网络(Wireless sensor network,WSN)主要功能为在网络中使用多个传感器可以独立去监测同一环境,并且将监测的结果分别传送至数据处理中心(Fusion center,FC),经由数据处理中心将结果进行处理分析,并做最后的判断。这已经在诸多工程中得到应用[ 1, 2, 3, 4, 5]。多数无线传感器的电力来源是电池,而电池的能源有限,因而电力消耗的控制是设计无线传感器网络的重点。针对三类最主要的电力消耗(观测过程消耗、CPU计算及控制消耗和数据传输过程消耗),已有不少的研究人员开展此方面的研究;如文献[6]仅考虑能耗与路由时间,根据RS-SI将网络划成不同区域,区域中的节点向其父节点发送数据直到sink,以此减低能耗;张瑞华等[ 7]为平衡网络能耗提出一种基于非均匀分簇的能量有效的无线传感网络路由算法(UCRA),包括非均匀分簇算法和最小能耗路由算法;Khajehnejad等[ 8]提出了基于单节点的重构算法,以提高网络传输的精度。文献[9]中指出由于数据转发的随机性将导致网络中各个节点的能耗并不均匀,寿命较短。单立群等[ 10]提出了一种将功率控制和数据聚合路由相结合的非凸优化模型以均衡各个节点的能量消耗;吴大鹏等[ 11]发展一种适用于无线传感器网络的协作压缩感知策略;王义君等[ 12]针对节点数目增多的实际情况提出一种能量有效的参考广播同步算法,结果显示也具有较低能耗。黄河等[ 13]提出了一种基于自适应加权的室内能量均衡路由算法,用于对系统过程的动态决策和判断;Ok等[ 14]提出的DEBR算法基于节点间能耗与剩余能量比值寻找一条从源节点到基站能量既充足又高效的路径,以追求网络能量平衡。另外,还有不少的能量较低的自适应方法已被用于无线传感器网络[ 15, 16]。已有的研究多数涉及控制传感器的开关,通过对每个传感器给予不同的排程,让传感器轮流关闭,以达到低消耗的目的。然而WSN系统判断的正确率与收到的观测值数量成正比,关机将导致观测值减少、系统实时性下降。此外每次重新打开传感器,都需要重新设定传感器,将增加额外的能耗浪费。近年来,一类新的只有当观测值可信赖时才传送信息给数据处理中心的传感器设计机制被提出来[ 16],这不仅能够节省能源,还能降低判断的错误率。本文提出了一种分布式WSN的多分段区域检查机制,并进行了仿真验证。
本文提出一个实时多分段区域检查机制的策略。其主要思路是将分布式无线网络按区段的信赖度,动态地分成多个分段区域,在不影响总体功能的基础上,通过对信赖度较低的区段降级运行达到系统节能的目的。信赖度评价的指标取决于各个区段发送到FC的能量强度,以及该区段信号的信噪比。为了节约能耗,对信赖度较低的区段主动降低传送给FC的能量强度,可以降低系统的总体能耗水平。在区域持续工作的过程中,信赖度可能是一个随机过程,动态的分段的组合不会影响系统的正常运行。
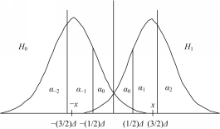
基于二元假设检验,当传感器端的观测值所给定事件H0 、H1 的条件机率很接近时,表示较容易判断错误,其中Zi 为第i个传感器所观测收到的信号值,而传感器端的准确率又限制了FC端的最终判断正确率。为此在本文提出的多分段区域检查机制中,将其分割为数个区段,并且每一个区段都会根据其信赖度被赋予不同大小的可能值α,以其提高其侦错能力。
α提出的想法在于认为当一信号落入到某个区段时,其必定会有在 H0下的机率以及在 H1下的机率,一般情况下,如果前半段决定为 H0时,则传送;若前半段决定为 H1时,则不传送;本文的作法则是根据信号落入区段的α值来调整送给FC的能量强度。
α值的确定如式(1)所示,其中x1 和x2为每一区段所分的边界:
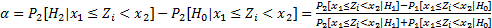 | (1) |
由此可见, 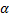
当x1 趋近于x2 时(Δ→0,Zj=x1),式(1)可简化为
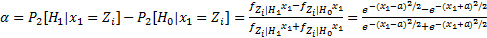 | (2) |
式中:α表示当事件发生时,环境最初送给每个传感器的信号。
对于图1所示的五个分段区域的第i个传感器端,判断后传送的值 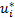
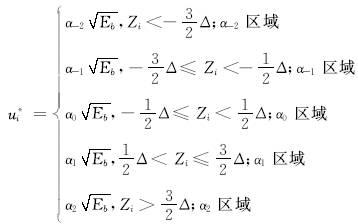 | (3) |
当x1 趋近于x2 时(Δ→0,Zj=x2),则传感器端对 
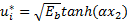 | (4) |
第i个传感器会把观测到的值Zi判断为 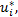
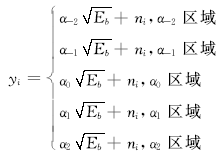 | (5) |
式中: 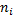
当事件发生时,经由传感器端第一次判断完后将其结果传送至FC端,但在无线通讯的环境中都存在噪声,噪声的存在可能会将其信息扭曲,以导致系统的效能变差,进而使得错误率提升。因此当传感器端加入了多分段区域检查机制后,FC端也必须有对应措施来防止其因噪声而产生的错误率提升。
当传感器端加入多分段区域检查机制后,传感器端传送的信息有可能为 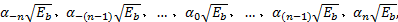
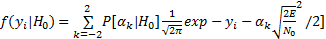 | (6) |
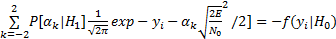 | (7) |
在传感器端本文采用最大后验概率(MAP规则)进行判断,具体表述为
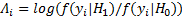 | (8) |
数据处理中心FC端使用最优控制(似然估计),此时的 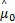
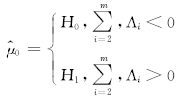 | (9) |
最优估计必须要有所有的P[αkH1]信息,在无法取得这些信息的时候,本文将选择改用次优化(Sub-optimal)的方式。以下是从最优算法推导到次优算法的近似值过程:
 | (10) |
式(10)第一次逼近使用到泰勒展开式的结果可取前两项为近似值 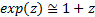
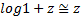
 | (11) |
最后,FC端使用次优化的等增益合并(EGC)方式进行判断, 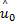
 | (12) |
WSN的信息传输过程可以描述为:首先,传感器判定事件信息所在的分段区域;然后,根据可信赖程度调整传送给FC的能量大小;接着FC使用次优化方法EGC的判断方式,将从传感器收到的信息yi直接全部加起来做最后的判断。但如果是在数据处理端FC使用最优方法进行判断时,则需要采用似然估计方式,根据传感器收到的信息yi计算出每个传感器的值,再将其全部加起来以做最后的判断。
依据图1所示的五分段区域结构可推导出每个传感器传送给FC端时,FC可能收到的实际信号yi的机率表示为
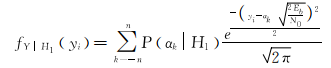 | (13) |
最后FC将所有传感器传送过来的信息全部相加,所得到的结果即是式(13)经过迭积的计算结果,其中W是FC从传感器所收到的值作相加的结果。m个传感器构成的WSN网络的情况如下:
 | (14) |
定义错误率 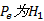
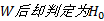
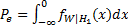 | (15) |
本文在实际模拟仿真过程中,采用数值分析的方法,其中EGC的处理方法是将传感器从-30到30这个区间分成6000个区段,依照式(13)分别算出落在每个小区段内的机率,再依照传感器的数目迭积起来,最后计算小于零的那些区段内的机率总和,即可得到最终的错误率。
同样地,采用MAP方法时也以类似的方法取得最终的错误率,也就是用式(13)算出来的机率并非落在 
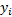
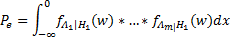 | (16) |
最后平均SNR的部分,传统为
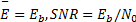 | (17) |
本文中采用的各种分区方式为
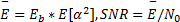 | (18) |
其中分区为3、4、5区最低错误率的分布方式情况下的可信程度值如表1所示。
| 表1 不同分区下的可信度值 Table 1 Confidence values in different partitions |
本节仿真过程的模拟环境使用16个传感器,分别对3、5、7区以及代表极大数目分区的50区方式,在次优控制算法与最优控制算法下对每个SNR值进行调整,取得此情况下的最低错误率。Y轴为最低错误率,X轴为平均SNR。
(1) x=1时,各种方法与传统方法的比较
图2给出了 x=1时,各种方法与传统方法的比较结果。由图2可看出, x=1时,分区越多错误率越低,最优控制方法的错误率明显小于次优方法,而且两类方法皆比传统方法好,与传统方法相比,只分三段的次优方法也有超过6.5 dB的增益,而最好的50段最优方法更有将近8.5 dB的增益;就错误率方面来看12 dB左右传统方式错误率已达到极限0.0009,而本文方法可达到0.0001以下。至于每条线在高SNR后都趋近于平坦的原因,是因为在高SNR时数据处理中心FC几乎不会出错了,但是传感器端依旧存在着错误。
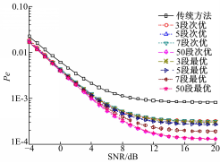 | 图2 x=1时不同分区方法与传统方法的比较Fig.2 Comparison among traditional methods and different partition methods where x=1 |
(2) x=1.8时,所发现的分区数目与错误率成正比状况
图3和图4分别给出了次优和最优判断方法下的不同分段的错误率。从图3和图4并结合其他数据可看出,分奇数区的错误率比分多区的偶数区的错误率更低,而此情况在最优方法下更加明显。这正是由于当初检查机制存在的原因,当收到的信号落在中间不明确的区域时,送出的任何信息都很可能会造成错误,而且在SNR越高时错误率越高,反之若在此情况什么都不送( α0=0),反而能抑制错误率升高,所以分奇数区时错误率更低。
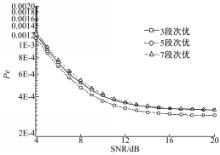 | 图3 x=1.8时次优方法三段至七段的错误率Fig.3 Error rate from section three to section seven in suboptimal method where x=1.8 |
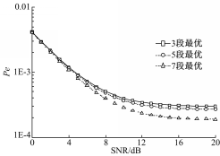 | 图4 x=1.8时最优方法三至七段的错误率Fig.4 Error rate from section three to section seven in optimal method where x=1.8 |
(3) x=5时,各种方法与传统作法的比较
图5为 x=5时各种方法与传统方法的比较结果。从图5可看出,在 x=5时表示前端已经非常明确了,每个传感器几乎不可能判断错误,此时很大机率传送的能量的是 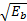
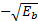
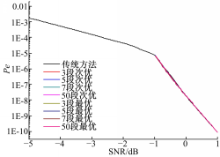 | 图5 x=5时不同分区方法与传统方法的比较Fig.5 Comparison among traditional methods and different partition methods where x=5 |
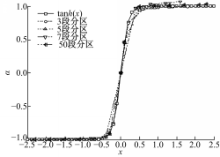
(4) x=1和5时,各种方法的 x值分布与tanh( x)的比较
图6和图7分别给出了不同方法下的 x值分布与tanh( x)的比较结果。从图6可以看到几乎所有的点都与tanh( x)线吻合,验证了式(2)。由图7可看到,当 x值是够大时奇数区只剩下三种值-1、0、1,而偶数区没有等于0的 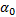
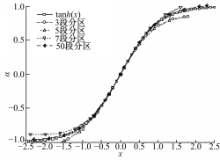 | 图6 x=1时不同分区方法的 α值分布与tanh( x)Fig.6 α value distribution in different partition methods and tanh( x)where x=1 |
(1)提出了多分段区域检查与软性决策系统,并将其应用于WSN系统;给出了在传感器端加入分任意区段的方式与给予可信赖度的方法,在FC端采用了软性决策的方式,实现了降低能量消耗与错误率的目标。
(2)在数据中心决策判断过程引入了基于最大后验概率的最优方法和基于等增益合并的次优方法,结果表明两种方法都有较高的仿真精度。
(3)分3、5、7段的分区通信仿真结果表明:多分区比以0为分界点分为两区方法更具有优势,但是分区过多也会造成效益的降低,采用5分段即可取得较好效果。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|