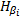崔金(1986),男,博士研究生.研究方向:无线通信,信号处理.E-mail:cuijintiger@163.com
提出了一种基于伪随机后缀的正交频分复用(Orthogonal frequency division multiplexing,OFDM)系统模型,并针对其在缓变信道下的信道估计需求,提出了一种基于一阶统计的信道估计方法和利用广义循环矩阵对角化性质的均衡方法。在高斯白噪声(Additive-white-Gaussian-noise,AWGN)信道、频率选择性衰落信道和多普勒信道下,对误码率性能进行了仿真分析。仿真结果表明:该方法适合缓变信道,其误码率性能优于传统插入导频的循环前缀(Cyclic prefix,CP)-OFDM;但对于多普勒信道其性能会变差。
A new model of orthogonal Frequency Division Multiplexing (OFDM) system based on pseudo-random-postfix was proposed. In view of the requirements of channel estimation under slow time-varying channel, a channel estimation method based on first-order statistics and a low-complexity equalization using the property of circular matrix diagonalization were proposed. The performance of Bit-Error-Rate (BER) was simulated and analyzed under the Additive-White-Gaussian-Noise (AWGN) channel, frequency selective fading channel and Doppler channel. The simulation results show that the proposed method can be applied to the slowly time-varying channels, such as the slow-moving case, and can achieve better BER performance than the traditional Cyclic Prefix (CP)-OFDM. However, the performance may get worse for the Doppler scenarios.
正交频分复用(Orthogonal frequency division multiplexing,OFDM)技术可以很好地对抗频率选择性衰落或窄带干扰,能消除信号多径传播所造成的符号间干扰(Inter symbol interference,ISI)[ 1, 2, 3, 4]。目前现有的OFDM主要是采取循环前缀Cyclic prefix,CP-OFDM方式。CP-OFDM虽然具有解调上的便利,但是降低了数据传输效率[ 5, 6, 7, 8, 9, 10, 11, 12, 13];并且由于信道估计的需求,需要在数据块中插入导频或训练序列以实时跟踪和估计信道,这进一步降低了系统的传输效率[ 11, 12, 13, 14]。
本文提出了一种新的OFDM模型,即伪随机后缀OFDM模型,无需插入导频和循环前缀,可实现低复杂度信道估计和迫零(zero forcing,ZF)均衡,可有效提高传输效率,可应用于缓变信道场景,且性能优于传统的CP-OFDM。
针对CP-OFDM的一些局限和不足,本文研究了一种基于伪随机后缀的OFDM模型。该模型以伪随机序列作为后缀,并利用后缀进行信道估计,可实现低复杂度信道估计和均衡。该模型利用接收向量的一阶统计量对信道进行半盲估计和跟踪,相比传统的OFDM无需单独发送导频,可显著提高传输效率;利用广义循环矩阵的性质[ 15]可进行低复杂度均衡。该方法对信道的估计具有一定的实时性,可以适应缓变信道。
下面给出伪随机后缀OFDM模型并介绍其原理。图1为N个子载波的 OFDM模型,第i个N×1的输入向量 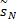
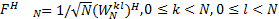 | (1) |
伪随机后缀 OFDM模型如图1所示。
后缀向量 c D =(c0,c1,…,cD-1)T与伪随机数α(i)相乘之后,作为后缀。并行宽度为P=N+D。
对应的P×1发送向量为
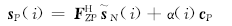 | (2) |
矩阵 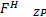
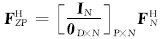 | (3) |
多径信道可等效为 L阶 FIR滤波器,冲激响应长度 L≤ D。它的传递函数表示为
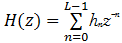 | (4) |
由循环矩阵定义[ 15],设 c0, c1,…, c n-1∈ C,有
 | (5) |
C称为数组 c0, c1,…, c n-1的循环矩阵。信道输入输出关系可用矩阵运算表达,接收向量等于发送向量与循环矩阵相乘。
根据信道对 OFDM符号的影响,可将信道矩阵拆分成 HISI( P)和 HIBI( P): HISI( P)是其下三角阵(包含对角线元素,第一列是[h0,h1,…,hL-1, 0,…,0]T),反映了 OFDM符号块间干扰; HIBI( P)是其上三角阵(不包含对角线,第一行是[0,…,0, h L-1,…, h1]),反映了符号块内干扰。
信号与信道卷积为
r p( i) = HISI( P) s P( i) + HIBI( P) s P( i-1) + n p( i) (6)
上式可以化为:
r p( i) =( HISI( P) +β i HIBI( P)) s P( i) + n p( i) (7)
式中: β i =α( i-1) /α( i)。
可令
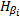
由广义循环矩阵的定义[ 15]有:
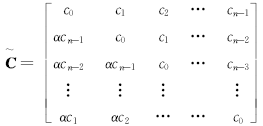 | (9) |
由以上定义, 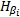
将式(2)带入式(7)可得第i个接收向量 r p( i)为
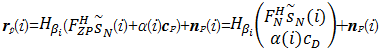 | (10) |
本文研究了一种基于一阶统计量的信道估计方法,该方法利用接收向量特定分量的一阶期望可完成信道估计。
这种算法的前提是信道是缓变的。因为算法本身利用了接收向量的一阶统计量,需要对一定时间间隔内的数据取期望,求期望的样本越多,效果越好。
设 HCIRC( D)是 D×D的广义循环矩阵,其第一行分量为[ h0,0,…,0, h L-1,…, h1]。
定义信号 s N( i)=[s0 (i),…,sN-1(i)]T,它的前 D个分量 s N,0( i)=[s0 (i),…,sD-1(i)]T;后 D个分量 s N,1( i)=[sN-D(i),…,sN-1(i)]T,根据物理意义,可将 HCIRC( D)分解为
HCIRC( D) = HISI( D) + HIBI( D) (11)
将式(6)展开,可得接收向量各分量为
r P( i) =
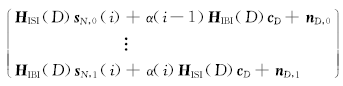 | (12) |
向量 r P( i)的前 D个分量和后 D个分量如式(12)所示。通常时域信号 s N( i)和高斯白噪声都是零均值的,对一定时间间隔内多个接收向量对应的分量求平均可使包含 s N,0( i)、 s N,1( i)和 n D,0、 n D,1的项趋近于零。故对接收向量的前 D个和后 D个分量取期望可得列向量 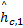
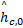
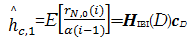 | (13) |
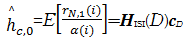 | (14) |
将两项相加后得到 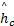
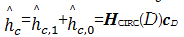 | (15) |
这样就把对接收向量特定分量求期望相加之后的新向量表示成循环矩阵和已知的后缀向量 c D相乘的结果。
由矩阵运算的性质,上式可化为式(16),其中 C D是第一行分量为[c0,cD-1,cD-2,…,c1]的循环矩阵, h D的元素是信道冲激响应函数 h n的前 D个响应值,即:
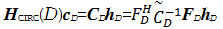 | (16) |
故信道冲激响应的估计量 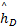
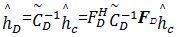 | (17) |
选取合适的后缀长度D,使其大于信道的冲激响应长度,即 L≤ D,这样就能保证对信道响应进行充分估计,从而利用接收向量的一阶统计完成半盲信道估计。
上面的方法适用于缓变信道,对于多普勒信道其性能会变差。
为消除多径效应带来的干扰,接收端需要对接收向量 r P( i)做均衡。均衡准则使用 ZF准则,其均衡器 GZF为
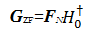 | (18) |
式中:(·) †为矩阵的Moore-Penrose伪逆矩阵[ 15]; H0为 P×N矩阵,它包含 HISI( P)的前 N列。
这里利用广义循环矩阵对角化的性质进行均衡。 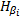
广义循环矩阵 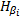
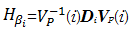 | (19) |
对角阵为
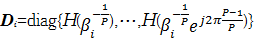 | (20) |
对角线元素 H( z)为
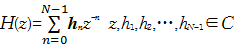 | (21) |
式中: h n =[ h1, h2,…, h N-1]中元素是信道时域冲激响应各点的值。
特征矩阵为
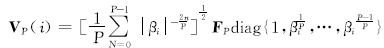 | (22) |
为使特征矩阵简化,将后缀中的 β i选为 β i = 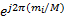
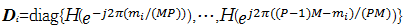 | (23) |
由 
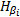
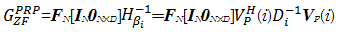 | (24) |
式(24)和 r P( i)相乘得:
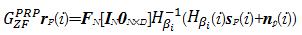 | (25) |
本文在美国MathWorks出品的Matlab R2011b软件环境下进行仿真。首先在AWGN信道下,对伪随机后缀OFDM系统误码率性能进行了仿真分析,重点比较该模型和插入导频的CP-OFDM的性能。
仿真中,OFDM系统参数设置如下:载波频率为2 .4 GHz;FFT点数为64;采样时间为200 ns;带宽为20 MHz;子载波调制为QPSK;子载波间隔为78 .125 kHz。
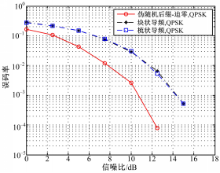
CP-OFDM的导频间隔取 N t =4和 N f =4。仿真结果如图3所示。从图3可看出,在AWGN信道下,模型的误码率性能好于CP-OFDM。
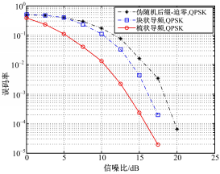
下面继续分析伪随机OFDM模型在频率选择性衰落信道下的误码率性能。仿真采用COST207 RA信道,仿真首先对数据做了信道编码,信道编码采用N =7的(133,171)卷积码,仿真性能如图4所示。
图4给出伪随机后缀OFDM系统和传统CP-OFDM算法的误码率比较。从图4中可看出,相比CP-OFDM,在10-4数量级下,伪随机后缀OFDM误码率性能大约有5 dB的提升。
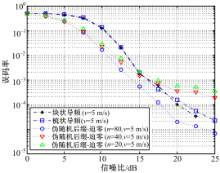
伪随机后缀OFDM模型的信道估计是通过取数个OFDM符号特定向量的期望,通过取期望消除偏差,估计出信道时域冲激响应,所以算法在多普勒信道下性能会变差,仿真分析算法在多普勒信道下的性能,结果如图5~图7所示。
从图5可知,在 v=5 m/s的情况下,由于多普勒频移较小,伪随机后缀OFDM信道估计算法在取符号数 n=80做信道估计时,误码率性能要好于CP-OFDM;而取 n=20和 n=40时, n=40的误码率性能略好。原因在于:此时运动速度较慢,多普勒频移较小,伪随机后缀OFDM信道估计算法中做一阶统计的符号数 n越多,越有利于消除偏差,性能越好,所以此时 n的取值越大,算法性能越好。
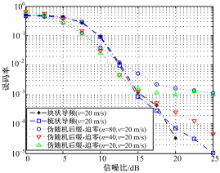
从图6可知,在 v=20 m/s的情况下,由于多普勒频移增加,信道的变化速度变快,伪随机后缀OFDM信道估计算法已逐渐不如CP-OFDM;其中, n=40的情况性能是最好的, n=20的情况性能略差, n=80时性能最差。原因在于:由于多普勒频移变大,信道的动态增加, n=80的信道估计算法不适应信道的快变,所以造成其误码率性能不理想;而 n=20的情况和 n=40的情况相比,其取期望值所用的符号数较少,相对信道跟踪能力会略强; n=40的情况,信道跟踪能力相比 n=20的情况会稍差,但是由于取期望值所用符号数更多,可以通过取期望消去更多偏差,所以此时性能会略好。
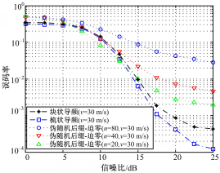
从图7可知,在 v=30 m/s的情况下,伪随机后缀OFDM性能已经明显不如CP-OFDM;其中, n=20的情况性能是最好的, n=40的情况性能略差, n=80的情况性能最差。原因在于:在 v=30 m/s的情况下,运动速度显著增加,信道估计算法的跟踪能力决定了系统的性能, n=20时其信道跟踪能力要强于 n=40和 n=80的情况,所以其性能在这几种情况中是最好的。
通过仿真分析,可知伪随机后缀OFDM模型在多普勒信道下,误码率性能变差,且在运动速度较快时,伪随机后缀OFDM模型信道估计取一阶期望的符号数越多,性能越差。
针对传统插入导频的CP-OFDM存在的问题,提出了一种基于伪随机后缀的OFDM系统模型,该模型相比CP-OFDM,无需插入导频,利用伪随机后缀作为保护间隔和进行信道估计,能达到有效提高传输效率的目的;但该方法的局限性在于:由于信道估计采用基于一阶统计的方法,虽然通过取期望可消除偏差,其在缓变信道下传输效率和性能相比传统CP-OFDM有所提高,但在多普勒信道性能有所下降,信道跟踪能力有限。本文仿真分析结果对OFDM信道估计方法在工程应用方面有参考意义。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|




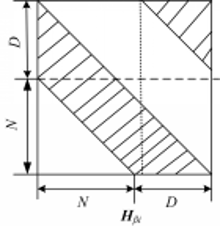
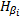 的形状
的形状