庄哲民,男,教授,博士.研究方向:智能信号处理,无线传感网络.E-mail:zmzhuang@stu.edu.cn
在研究已有的块稀疏信号贪婪算法的基础上,提出一种正则化的自适应恢复算法。该算法在块稀疏度未知的前提下,添加了正则化的思想进行块挑选,从而更正确地挑选出块信号的支撑块,实现信号的重建。该算法首先在确定块的稀疏度和选择步长后,利用相关最大化原则实现支撑块的初次挑选;然后,依据已挑选出的支撑块再进行正则化分组,实现二次挑选;最终通过循环迭代正确挑选出整个信号的支撑块。通过仿真实验证明,该算法不仅不需要信号的块稀疏度作为先验知识,且较现有的块信号贪婪算法的重构概率更高,也比现有的块稀疏自适应贪婪算法所需的迭代次数更少和迭代时间更短。
A regularized adaptive matching pursuit algorithm as proposed after research and summarize the existing greedy algorisms based on block-sparse signal. This algorithm mainly in the light of regularized method under a condition that a block-sparse degree is unknown, so that the signal support set can be determined more accurately by the algorithm, then we can reconstruct a signal precisely. First, the algorithm initializes a sparsity degree and step size of a block signal; by maximizing the correlation between residual and measurement matrix, it realizes the selection of subset of the signal support. Then the algorithm updates the selected subset in the second time. Finally, the exact support set is acquired through iteration. The experimental results prove that the proposed algorithm can get better reconstruction performance than other existing greedy algorithms based on block signal, and it has less iteration number and iteration time than the other adaptive algorithm based on block signal.
重构算法是压缩感知[ 1]的重要组成部分,其主要体现为一个范数最小模型的求解过程,贪婪追踪法是一种得到广泛应用的求解该过程的算法之一,它的核心思想是选取与残差信号最相似的原子,其典型的代表是匹配追踪(MP)[ 2]和正交匹配追踪算法(OMP)[ 3],Needell为了能够让算法更精确地挑选信号的支撑集,提出了正则化匹配追踪算法(ROMP)[ 4],但是,在信号重构的过程中,信号的稀疏度往往是未知的。Do等[ 5]提出了自适应匹配追踪算法(SAMP),但是,针对特殊的模型,例如块稀疏信号(Block-sparse signal),用传统的匹配追踪算法不但效率低,而且其重构效果也较差。因此,国内外很多学者都在这些传统算法的基础上探求进一步的应用,文献[6]提出了基于块信号的匹配追踪算法(BMP)和基于块信号的正交匹配追踪算法(BOMP),但其支撑块的挑选过程缓慢,至少需要 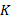
本文提出了基于块稀疏信号的正则化自适应压缩感知算法,该算法在块稀疏度未知的前提下,增加了正则化的挑选方法,重新定义了支撑块的挑选过程,最终在满足迭代收敛条件的情况下,精确地恢复原信号。仿真实验也表明,本文算法在保证迭代次数和恢复时间的前提下,提高了信号的重构概率。
在压缩感知理论的重构问题中,由于观测数M远小于信号长度N,因此需要求解欠定方程Y=ACS X,其本质上就是要找到一个最稀疏向量作为方程最后的解,即解决下式的优化问题:
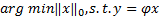 | (1) |
式中: 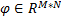
以上论述的是压缩感知的一般模型,其中原信号 x仅有的 k个非零值是离散分布的,但实际中原信号具有块稀疏结构的信号(Block-sparse signal)非常多,例如DNA阵列、多频带信号、雷达脉冲等。因此,针对这种特殊的信号模型结构,研究特殊的理论算法具有实际的意义。把式(1)中 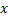
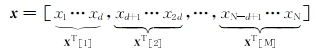 | (2) |
由式(2)可知把信号分为M个块信号,例如x[t]被称为第t个块信号,每个块信号的长度为d,N=M*d,显然,当d=1时,块稀疏信号就会变成正常结构的信号;文中定义块稀疏度为k,即x[t]最多有k个不为0的欧几里德范数,表示为
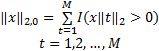 | (3) |
式中: 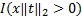
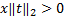
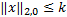
测量矩阵 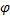
 | (4) |
本文的算法主要分为块初始化、支撑块初次挑选、正则化挑选、支撑块更新和残差更新这五个步骤。在块初始化中,衡量测量矩阵分块有效性的两个重要性质分别是块相关性和块的RIP特性;其中块相关性是分块测量矩阵最重要的基本量,块相关系数的计算公式 μB如下所示[ 9]:
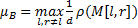 | (5) |
μB越小,测量矩阵中的相关性就越小,这里的 ρ(•)为谱半径,且
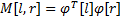 | (6) |
式中:M[l,r]是大小为d*d的块信号,从文献[9]可知块相关系数的两个定理:
定理1 块相关系数应满足0≤μ_B≤μ,μ∈[0,1]。
定理2 如果 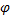
另外,初始化时构建的测量矩阵满足RIP性质是块稀疏重构中的必要条件,当φ∈RM*N,Ω={φ1,φ2,…,φM}时,根据文献[ 10]可得块的RIP条件如下:
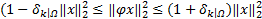 | (7) |
显然 δk|Ω表示块信号的RIP常量,当一个信号的稀疏度为m,而它的块稀疏度为k,则有 δk|Ω≤δm,文献[ 10]指出如果 φ满足 δ2k|Ω<1,则式(1)中的重构信号 x有唯一解。
本文在块初始化过程中,选择高斯随机分布矩阵作为测量矩阵,并将其分块[ 11];高斯随机分布矩阵是一个独立性非常强的矩阵,矩阵中每个元素都是独立分布的[ 12],因此列分块后的每个块元素都是不相关的;且文献[ 10]通过理论证明高斯随机分布矩阵满足RIP性质,而当分块大小为d(d≥1)时,块稀疏度为k的向量只是普通意义下的k_d 稀疏向量,因此,高斯随机分块测量矩阵满足信号稀疏度为kd的RIP特性。
文中支撑块的挑选分为两个步骤:分别利用相关最大化和正则化原则进行挑选;本文算法较其他块稀疏信号恢复算法最新颖的一步是添加正则化方法对支撑块实行挑选,其方法是利用式(8)将块索引集 J所对应的块原子的相关系数分成若干组:
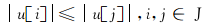 | (8) |
它的关键就是挑选出能量最大的一组相关系数所对应的块原子索引值,并将其存入更新的支撑块集合 J0中,从而实现对块原子的二次筛选;添加正则化方法使本文最多经过 K次迭代便可得到一个块原子数小于2 K的块支撑集,此支撑集用于精确重构信号,对于没有选入块支撑集的块原子,此正则化过程则能保证它们的能量一定远小于被选入的块原子的能量,从而提高信号重构的可靠性。
本文算法的主要思想是在块稀疏度未知的前提下,设定迭代步长,将正则化思想引用到支撑块的挑选中,算法的具体步骤如下:
(1)块初始化:高斯随机分布测量矩阵 φ∈RM×N,原信号x,观测信号y,初始信号的块稀疏度k,块长度d,设定算法迭代误差 δ,并分别将分块测量信号和分块原信号记为 φ[t]和x[t],信号残差r0=y,步长step=1,阶段长 S=1。
(2)支撑块初次挑选:利用相关最大化的挑选原理,在每次迭代中选出与残差rl-1相关最大的s个块信号的下标,其挑选公式为
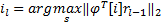 | (9) |
(3)每一次挑选块的个数由步长step控制,并将挑选出的原子il 存储在J中,以备下一步再次挑选。
(4)正则化筛选:其根本的思想是先通过式(8)将步骤(2)中得到的支撑块分组,然后选择能量最大的一组对应的块索引值存入J0中。
(5)更新支撑块:令T=T⋃J0 。
(6)更新残差:利用式(10)计算残差
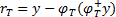 | (10) |
若 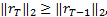
(7)输出重构向量:当迭代数大于块的分组数或者残差小于迭代误差 δ时,迭代结束,输出重构向量
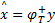 | (11) |
本文算法采用转换阶段的方式逐步增加支撑块数量,将同一个迭代过程分成多个阶段,通过可变步长逐步调整块的挑选个数,不仅解决了BMP和BOMP[ 6]每次只挑选一个支撑块而引起的效率低下问题,也解决了文献[6-7]中块稀疏度需要预估计的问题;同时,为了提高每一次挑选出的支撑块的准确性,加入了正则化挑选方法(步骤(3)),保证了挑选出来的块能量一定大于没被挑选的块能量,从而提高了支撑块的挑选效率,增加了信号的重构概率。
目前国内外基于贪婪追踪的块稀疏信号恢复算法主要有BMP、BOMP、BCoSamp和BSAMP,因此,本文算法主要与这些算法在重构概率上作出对比,并加以分析。实验的步骤如下:
(1)分块:先设定测量矩阵 φ∈RM×N(M=80,N=160)为高斯随机测量矩阵,原信号x为N阶的零矩阵;然后将两者分为k(k=20)块,每个块的长度d=8,块稀疏度k=1,2,…,12;最后根据块稀疏度随机挑取原分块信号中的k个非零块,赋予其高斯随机分布值。
(2)步长设定:为了增加重构信号的精确度,对于BSamp[ 8]和本文算法,均设定初始步长step=1,阶段长 S=1。
(3)重构标准:分别取块稀疏度k=1,2,…,12,对在每个块稀疏度下的重构算法都运行500次,设定 δ=10-5,对于重构的块信号 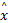
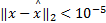
实验结果如图1所示。由图1可见,本文算法在块稀疏度为6的情况下仍然保持100%的恢复效率,但其他几种算法的重构概率已经大大降低,而BMP已经完全不能实现块稀疏信号的重构;在块稀疏度为7时,本文算法重构概率比BOMP提高了8.5%,比BCoSamp提高了132.57%;在块稀疏度为8时,本文算法仍然略高于BOMP和BCoSamp;相对于另一种块稀疏自适应迭代算法(BSAMP),在块稀疏度为6时,BSAMP已经下降至18.4%,而本文算法仍能100%重构,比BSAMP提高了4.43倍;当BSAMP在块稀疏度为7时,重构概率下降为0,而本文算法仍有81.4%的重构概率。综上所述,作者提出的基于块稀疏信号的正则化自适应算法的重构概率不仅远大于另一种基于块稀疏的自适应算法,并且相对于其他的3种算法也有明显的提高。
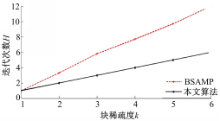
目前,基于块信号的自适应贪婪算法只有BSAMP[ 8],下面将本文算法和BSAMP算法的复杂度加以对比;信号和测量矩阵的分块、步长和重构标准的设置如上所述,算法在每个块稀疏度正确重构200次的基础上,分别从算法的平均迭代次数和平均运行时间上比较分析两种算法的复杂度,实验结果如图2和表1所示。
| 表1 重构时间对比 Table 1 Comparison of reconstruction time |
由图2可见,本文算法的迭代次数随着块稀疏度k的变化满足O(k),而BSAMP则基本满足O(2k),也就是迭代次数为本文算法的两倍。由于两种算法的初始化过程都是一样的,因此,表1是除去块信号初始化的时间统计。由表1可以看出,两种算法在 k=1时的重构时间基本相等,到 k=6时BSAMP约为本文算法重构时间的12.6倍,可知,随着块稀疏度的增加,本文算法的重构时间只是略微增加,而BSAMP的重构时间是成倍增加。综上所述,无论从迭代次数还是迭时间,本文算法都比BSAMP的复杂度更低。
由以上实验分析可知,本文添加了正则化的挑选方法,让支撑块在每次迭代都经过两轮挑选,使支撑块的挑选过程更为严格,相比于目前基于块稀疏的贪婪算法,本文算法在提高支撑块挑选准确性的同时,不仅提高了算法的重构概率,也降低了算法的迭代次数和迭代时间。
针对块稀疏结构信号,在块稀疏度未知的前提下,提出一种新的基于块稀疏信号的正则化自适应压缩感知算法,用于块稀疏信号的重构,同时将算法与另一种块稀疏自适应贪婪算法(BSAMP)作对比。实验结果表明,在满足信号重构误差的前提下,本文算法的迭代次数比BSAMP算法要少,迭代时间比BSAMP算法要短,其中迭代次数比BSAMP算法少一倍。随着块稀疏度的增加,BSAMP算法的重构时间不断递增,而本文算法的重构时间则基本稳定,远低于BSAMP算法,运算具有较好的鲁棒性。因此,本文算法中支撑块的挑选过程比文中的其他几种方法更有效,能较好地运用在块稀疏信号的重构上。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|