引用本文
刘玉春, 王俊, 张各各. 改进的基于MSR二维谱的OMEGA-K双基SAR成像算法. 2014, 44(1): 264-269
LIU Yu-chun, WANG Jun, ZHANG Ge-ge. Modified OMEGA-K imaging algorithm for bistatic SAR based on MSR 2D spectrum. 吉林大学学报(工学版), 2014, 44(1): 264-269  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
改进的基于MSR二维谱的OMEGA-K双基SAR成像算法
刘玉春1,2, 王俊1, 张各各1
1.西安电子科技大学 雷达信号处理国家重点实验室,西安 710071
2.周口师范学院 物理与电子工程系,河南 周口 466001

刘玉春(1979),男,博士研究生.研究方向:双基SAR成像和无源雷达成像.E-mail:lycdgp@163.com

基金:国家部委预研基金项目(9140C010507100C01); “863”国家高技术研究发展计划项目(2010AAJ144);
摘要

提出了一种改进的基于级数反演(MSR)二维谱的双基合成孔径雷达(SAR)OMEGA-K成像算法。在双基SAR OMEGA-K算法的基础上,通过在距离频域方位时域内的斜距历程高阶项对消处理,使回波信号二维谱和基于低阶泰勒展开的MSR二维谱相匹配,进而采用OMEGA-K成像算法实现聚焦成像。仿真实验中,在斜距历程同为二阶展开的情况下,改进的OMEGA-K算法的聚焦效果要优于常规OMEGA-K算法,而与三阶泰勒展开时的常规OMEGA-K算法聚焦效果非常接近,表明该算法在斜距历程低阶泰勒展开的情况下可以取得较好的聚焦效果,能够降低算法的复杂度。

关键词: 通信技术; 双基合成孔径雷达; 成像算法; OMEGA-K
中图分类号:TN957.52 文献标志码:A 文章编号:1671-5497(2014)01-0264-06
Modified OMEGA-K imaging algorithm for bistatic SAR based on MSR 2D spectrum
LIU Yu-chun1,2, WANG Jun1, ZHANG Ge-ge1
1.National Key Laboratory of Radar Siganl Processing, Xidian University, Xi'an 710071, China
2.Department of Physics and Electronic Engineering,Zhoukou Normal University,Zhoukou 466001,China
Fund:
Abstract

A modified OMEGA-K imaging algorithm is proposed to reduce the computational complexity of the Method of Series Reversion (MSR) 2D point target spectrum for the bistatic Synthetic Aperture Radar (SAR). By performing the cancellation of the high order term of range history in range-frequency azimuth-time domain, 2D point target spectrum can be matched with low order Taylor expansion of echo signal, so that the focused imaging can be achieved by the OMEGA-K algorithm. The simulation results indicate that the modified OMEGA-K for range history approximated by second order Taylor expansion can achieve better focused performance than that of conventional algorithm for range history approximated by second order Taylor expansion, and approach the performance of the conventional algorithm for range history approximated by three order expansion. This demonstrates that the proposed algorithm has a good focusing performance by low order Taylor expansion, thus lowers the computational complexity.

Keyword: communication; bistatic synthetic aperture radar; imaging algorithm; OMEGA-K
0 引言

二维谱求解是双基合成孔径雷达(SAR)成像的基础和难点问题。LBF算法[ 1]在同构双基SAR情况下具有较好的成像效果,但由于对收发相位历程采取平均截断处理,导致其在异构平台构型下存在较大误差。文献[ 2]对LBF算法进行了改进,利用瞬时多普勒贡献率对相位历程进行加权处理,提高了二维谱的精确性。文献[ 3]应用LBF算法的思想,在处理过程中应用二维驻相原理,得到了具有较高精度的二维谱,可以方便地应用在距离多普勒(RD)和线频调变标(CS)成像算法中。级数反演(MSR)二维谱算法[ 4]采用级数反演技巧,精度可以通过泰勒展开级数的阶数控制,聚焦性能优良。在二维谱求解算法的基础上,成像算法也相继出现。文献[ 5]提出基于LBF二维谱的逆尺度傅里叶变换(ISFT)双基SAR成像算法。文献[ 6]提出基于ELBF二维谱的平行等速构型双基CS算法。文献[ 7, 8]分别提出基于MSR二维谱的方位不变构型双基RD和双基OMEGA-K成像算法。在这几种较为典型的成像算法中,由于MSR二维谱相比其他频谱(LBF、ELBF)更精确,并且OMEGA-K成像算法与其他算法(RD、CS、NLCS)相比精度较高,故而文献[8]提出的算法具有较好的聚焦效果。但文献[ 8]采用了MSR二维谱,为了取得较高精度,需要把斜距历程高阶泰勒展开,而其二维谱也要保留至高阶,增加了算法的复杂度。

综上,现在的双基成像算法存在分辨率不高[ 5, 6]和算法复杂[ 7, 8]等问题。基于此,本文在文献[ 8]的基础上提出一种改进的基于MSR二维谱的双基OMEGA-K成像算法。为了提高成像分辨率,本文采用较为精确的MSR二维谱和具有较高成像精度的OMEGA-K成像算法。为了降低算法复杂度,要尽量降低求解二维谱时斜距历程的泰勒展开阶数,因此算法在距离频域方位时域内对回波信号进行了高阶项对消处理,使回波信号的二维谱与MSR二维谱在斜距历程低阶展开时相匹配,以达到在低阶泰勒展开情况下取得较好聚焦效果的目的。

1 基于MSR二维谱的双基OMEGA-K成像算法

假设发射机信号为chirp信号,参考点回波信号解调后可以表达为

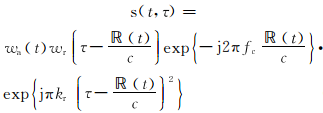(1)

式中:w r(τ)为脉冲包络;w a(t)为收发天线的方向图函数;k r为脉冲调频率;c为光速;t、τ分别代表慢时间和快时间;fc为载频; 为斜距历程。

根据文献[ 4],参考点目标的MSR二维谱为

(2)

式中:W r(fr)表示距离时间频率谱包络;W az_ ref(fa)表示多普勒谱包络;f r和f a分别为距离频谱和多普勒频率。

二维参考频谱的相位为

(3)

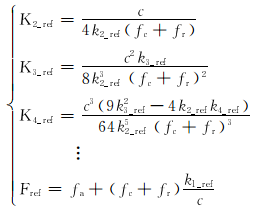(4)

式中:R cen_ref为零方位时刻的双程斜距;kn _ref为零方位时刻斜距历程的第n阶距离导数,其表达式为

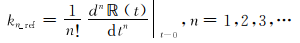(5)

根据文献[ 8],双基OMEGA-K成像算法的关键步骤之一是构造距离映射函数。应用角度不变假设(即假设在某成像区域内,系统的几何结构变化很小,可以忽略,此区域被称为不变区域),认为在不变区域内收发平台的斜视角不变。

同理,假设在不变区域内有一散射点A,则其回波信号的二维谱为

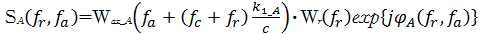(6)

(7)

OMEGA-K算法的第一步为参考函数相乘(RFM),即

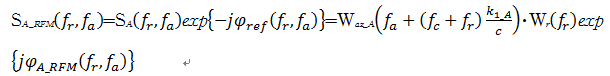(8)

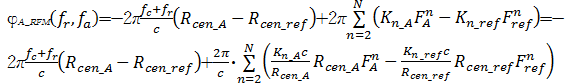(9)

式(9)中

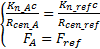(10)

式(10)证明见附录A。

式(9)也可以写为

(11)

在式(11)中,令括号内各项等于f c+f' r,即得到了距离频率映射函数

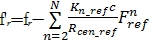(12)

式中:f'r表示经过频率映射后的距离频率。

根据式(12),利用Stolt插值进行距离频率映射后,式(11)变为

(13)

然后经过二维逆傅里叶变换就得到散射点A的像。

2 改进的双基OMEGA-K成像算法

由上述分析知,如果斜距历程泰勒展开的级数较高,算法复杂度会提高。反之,如果仅作低阶展开,所得二维谱又不够精确,聚焦效果不佳。为了平衡此矛盾,提出一种改进的OMEGA-K双基SAR成像算法。

首先对式(1)作距离向傅里叶变换,可得

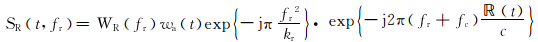(14)

假设在式(14)中,斜距历程被N阶泰勒展开,即

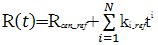(15)

其中N取大于等于2的整数。又有

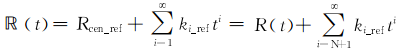(16)

从式(16)可以看出,N阶泰勒展开的斜距历程忽略了真实斜距历程的高阶项,这给聚焦成像带来误差。为了消除此误差,令高阶项对消相位为

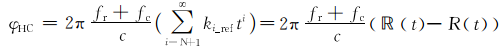(17)

高阶项对消操作为

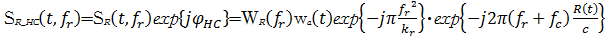(18)

从式(18)可以看出,参考点的回波信号通过高阶项对消操作,消除了斜距历程高阶项的影响,使其二维谱和MSR二维更加匹配。需要指出的是,对于非参考点的散射点,在高阶项对消操作中是以参考点的高阶项作为其高阶项进行了近似处理。这种处理是合理的,因为高阶项是时间的慢变函数,可以忽略其在不变区域内的变化,所以用参考点的高阶项来代替其他散射点的高阶项进行对消。

对式(18)做慢时间维的傅里叶变换,即可得到经过高阶项对消操作后回波信号的二维谱:

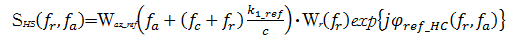(19)

(20)

虽然式(19)(20)与式(2)(3)形式上一致,但是二者的物理意义并不相同,因为经过高阶项对消操作,斜距历程高阶项对二维谱的影响减少了,式(19)(20)与斜距历程N阶泰勒展开的MSR二维谱更为匹配。在此基础上,可以采用基于N阶泰勒展开MSR二维谱的OMEGA-K算法对散射点进行成像。

从上面的分析可以看出,经过斜距历程高阶项对消处理,MSR二维谱与回波信号的频谱更为匹配,因此改进的OMEGA-K成像算法可以在低阶斜距历程、低阶泰勒展开的基础上取得较好的聚焦效果。

3 两种算法之间的关系

两种算法的流程图如图1所示。

图1 两种算法的流程图Fig.1 Flow chart of two algorithms

相同点:两种算法在聚焦过程中都采用了OMEGA-K成像算法,通过RFM完成一致聚焦,通过Stolt插值来完成残余方位压缩、残余距离徙动校正、残余耦合项补偿等操作。

不同点:①处理流程不同。相比OMEGA-K算法,改进的OMEGA-K在二维傅里叶变换中增加了高阶项对消操作;②处理思想不同。基于MSR二维谱的OMEGA-K算法通过控制泰勒展开式的阶数来保证二维谱的精确性,而改进的OMEGA-K算法除了采用MSR二维谱外,还通过高阶项对消操作使回波信号与MSR二维谱更加匹配。简言之,OMEGA-K算法中MSR二维谱与回波信号“单向”匹配,而改进的OMEGA-K算法中二维谱与经过高阶项对消的回波信号“双向”匹配。

从图1可以看出,改进的OMEGA-K算法与OMEGA-K算法相比,处理流程稍稍复杂。其中改进的OMEGA-K算法的第一步(距离向傅里叶变换)和第三步(方位向傅里叶变换)仅仅是相当于把OMEGA-K算法中的第一步(二维傅里叶变换)分开来,复杂度并没有增加。也就是说,在距离历程同阶泰勒展开的情况下,改进的OMEGA-K算法仅仅比OMEGA-K算法多了高阶项对消一步。从式(18)可以看出,这一步是相位相乘操作,增加的运算量很小。

通过高阶项对消处理,以增加很小运算量的代价,使回波信号和二维谱更加匹配,达到在低阶泰勒展开情况下取得较好的聚焦效果的目的,降低整个算法的复杂度。

4 仿真和分析

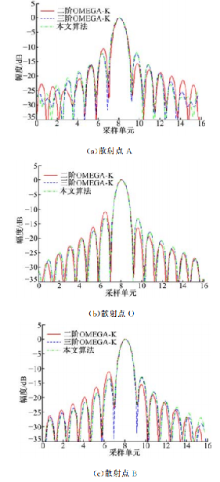
利用改进的OMEGA-K算法对星载双基SAR进行仿真,仿真参数如表1所示。对O、A、B三个散射点进行聚焦成像,其中O点为参考点,坐标为(0,0,0);A点坐标为(-600,-600,0),B点坐标为(600,600,0);坐标单位为米。仿真使用了3种成像算法,分别是斜距历程泰勒展开为2、3阶时的OMEGA-K成像算法;2阶泰勒展开时改进的OMEGA-K算法。仿真结果分别如图2和表2所示。

表1 仿真参数 Table 1 Simulation parameters

从图2可以看出,应用泰勒二阶展开的OMEGA-K成像算法,由于二维谱与回波信号的失配,导致聚焦性能恶化,左右副瓣出现了严重失衡。而采用基于二阶泰勒展开的改进的OMEGA-K算法,有效改善了上述性能恶化,其剖面图曲线基本上与基于三阶泰勒展开的OMEGA-K算法重合。因为基于二阶泰勒展开OMEGA-K算法左右副瓣的失衡,所以表2给出了左右两侧的峰值旁瓣比(PSLR)。从表2中可以看出,基于二阶泰勒展开的OMEGA-K成像算法的左右PSLR相差为4~6 dB。通过高阶项对消操作,在同为二阶泰勒展开的情况下,改进的OMEGA-K算法左右两侧的PSLR相差仅在0.3 dB之内,与基于三阶泰勒展开的OMEGA-K算法基本一致。而改进的OMEGA-K算法的冲激响应宽度(IRW)也与基于三阶展开的OMEGA-K一致。实验表明改进的OMEGA-K算法有效提升了聚焦性能。

表2 三种算法成像效果 Table 2 Imaging quality of three algorithms

图2 三种算法成像结果(方位向剖面)Fig.2 Imaging results of three algorithms (azimuth profile)

5 结束语

改进的基于MSR二维谱的OMEGA-K双基算法通过高阶项对消处理,使回波信号的二维谱与MSR二维谱更加匹配,从而提高了算法的聚焦性能。应用改进的OMEGA-K成像算法,可以在斜距历程在低阶泰勒展开的情况下取得较好的聚焦效果,实现降低算法复杂度的目的。本文算法主要应用于小场景成像中。在大场景情况下,利用参考点的回波信号进行高阶项对消操作会给场景边缘目标带来较大误差,所以需要进行分块处理。

The authors have declared that no competing interests exist.

参考文献
[1] Loffeld O, Nies H, Peters V, et al. Models and useful relations for bistatic SAR processing[J]. IEEE Trans Geosci Remote Sens, 2004, 42(10): 2031-2038. [本文引用:1]
[2] Wang R, Loffeld O, Ui-Ann Q, et al. A bistatic point target reference spectrum for general bistatic SAR processing[J]. IEEE Geosci Remote Sens Lett, 2008, 5(3): 517-521. [本文引用:1]
[3] Wang R, Deng Y, Loffeld O, et al. Processing the azimuth-variant bistatic SAR data by using monostatic imaging algorithm based on two-dimensional priciple of stationary phase[J]. IEEE Trans Geosci Remote Sens, 2011, 49(10): 3504-3520. [本文引用:1]
[4] Neo Y, Wong F, Cumming I. A two-dimensional spectrum for bistatic SAR processing using series reversion[J]. IEEE Geosci Remote Sens Lett, 2007, 4(1): 93-96. [本文引用:2]
[5] Natroshvili K, Loffeld O, Nies H, et al. Focusing of general bistatic SAR configuration data with 2-D inversescaled FFT[J]. IEEE Trans Geosci Remote Sens, 2006, 44(10): 2718-2727. [本文引用:2]
[6] Wang R, Loffeld O, Nies H, et al. Chirp scaling algorithm for the bistatic SAR data in the constant-offset configuration[J]. IEEE Trans Geosci Remote Sens, 2009, 47(3): 952-964. [本文引用:2]
[7] Neo Y, Wong F, Cumming I. Processing of azimuth-invariant bistatic SAR data using the range Doppler algorithm[J]. IEEE Trans Geosci Remote Sens, 2008, 46(1): 14-21. [本文引用:2]
[8] Liu Bao-chang, Wang Tong, Wu Qi-song, et al. Bistatic SAR data focusing using an OMEGA-K algorithm based on method of series reversion[J]. IEEE Trans Geosci Remote Sens, 2009, 47(8): 2899-2912. [本文引用:5]