根据文献^{[ 8]}可知,基于单环掺铒光纤激光器在附加一个延迟项的同时可以产生混沌。系统的状态方程可以表示成如下形式:

(1)

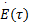
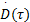
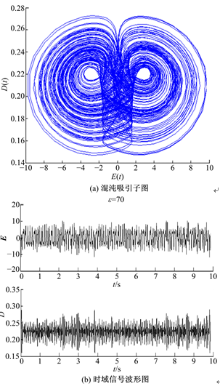
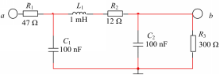
式中:E表示输出激光场强; 表示E对 τ的微分;D表示反转粒子数; 表示D对 τ的微分;k表示损耗系数;g表示增益系数;I_p表示泵浦光强; 表示延迟反馈光路的延迟率; τ₀表示延迟的归一化时间,文献^{[ 8]}给出系统初值为: k=1000, g=4700, I _p=4, τ₀=0.01,并且给出证明,在 ε<92区间内,系统工作在混沌状态。

按照式(1)中的运算关系和文献^{[ 8]}给出的初值,在Matlab中解微分方程,选取 ε=70,如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 仿真结果图Fig.1 Simulation results

按照系统状态方程设计电路,整个电路包含两部分,一部分是基本电路设计,包括加法电路、乘法电路和积分电路,取 ε=70,设计电路如图2所示;另一部分是延迟线设计,采用LC电路实现延迟,如图3所示。通过对图中模拟电路的计算,可以得到如下计算公式:

(2)

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 单环掺铒光纤激光器混沌的模拟实验主电路图Fig.2 Circuit of single-ring erbium-doped fiber laser chaotic systems

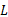
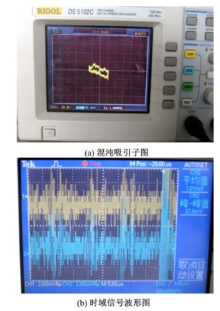
应用文献^{[ 9]}中的方法设计延迟电路如图3所示。因延迟时间非常短,只采用一级的LC电路,LC的值如图3中标示,其中 具有12 Ω的直流电阻。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 延迟电路图Fig.3 Delay circuit diagram

混沌吸引子如图4(a)所示, 和 的时域波形如图4(b)所示。由以上两组实验可知,仿真结果与实验结果基本一致,所以可用模拟电路替代单环掺铒光纤激光器。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 实验电路结果Fig.4 Experimental circuit results

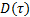
在模拟电路中得到的时域信号波形需要进行一系列的后续处理,产生真随机序列,若要应用在图像加密方面,还要对真随机序列进行检测,看其统计特性是否具备随机性。采用NIST随机性测试软件包进行测试,此软件包共有16项测试,在检验中,选取1000组长度为10⁵bit的生成序列进行试验,结果通过了全部16项测试,但因篇幅限制,仅列出最重要的5项测试数据,如表1所示。

表1

Table 1

表1(Table 1)

表1 真随机数测试结果 Table 1 True random number test results 测试名称 P-value 通过率/% 判定结果 频率检验 0.963656 99.83 随机序列 块内频数检验 0.504327 98.45 随机序列 游程检验 0.768545 98.91 随机序列 离散傅里叶变换检验 0.809763 99.97 随机序列 近似熵检验 0.339480 99.01 随机序列

表1 真随机数测试结果 Table 1 True random number test results

图像加密过程是基于Matlab7.1平台进行的,选取256×256像素的Lena图像作为加密对象,如图5(a)所示,混沌序列由模拟电路产生,加密步骤分为置乱和扩散两部分,具体步骤如下:

(1)混沌电路产生的连续信号经采样得到序列D(i)和E(i),利用式(3)对D(i)和E(i)进行预处理:

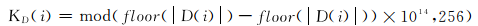(3)

式中:M为图像行数;N为图像列数,i=1,2,…,L,K_D (i)∈[0,255],L=M×N。

(2)用Arnold映射对原图像进行置乱操作,得到置乱后序列P(i),i=1,2,…,L。

(3)对置乱后序列 进行加密,采用如下加密公式:

(4)

(4)变换C(i)序列为加密图像,加密结果如图5(b)所示。

解密过程是加密过程的逆过程,不再赘述。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 图像加密效果Fig.5 Image encryption effect

2.3.1 密钥空间分析

本文所用的混沌系统是一个二维的方程组,产生两个序列,这两个序列分别有两个初始条件,即E(0)和D(0),当计算精度为10^-16时,产生的密钥空间为10³²,如果再加上控制参数等其他条件,那么密钥空间就至少大于10³²,在这样大的空间里,足以抵御穷举攻击。

2.3.2 统计分析

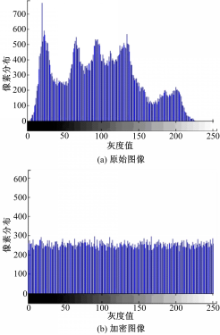
统计分析分为直方图分析和相邻像素相关性分析。从图6(b)可以看到,加密图像的直方图呈均匀分布,很好地掩盖了原始图像的统计结构,使攻击者无法从统计直方图下手分析图像。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 图像统计直方图Fig.6 Histogram image

至于相关性分析,采用式(5)计算水平、垂直、对角三个方向的相关系数,计算结果如表2所示。

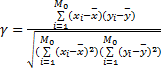(5)

式中:x_i和y_i分别表示图像中第i对邻居像素的两个像素值; 分别为所有x_i、所有y_i的平均值;M₀ 为选取的相邻像素对组数;γ为相邻像素的相关系数。

表2

Table 2

表2(Table 2)

表2 相关系数 Table 2 Correlation coefficient 方向 原图像 加密图像 水平 0.924 0.00095 垂直 0.961 -0.00088 对角 0.937 -0.00136

表2 相关系数 Table 2 Correlation coefficient

从表2可知,原图像在三个方向上高度相关,而加密图像相关系数接近于0。

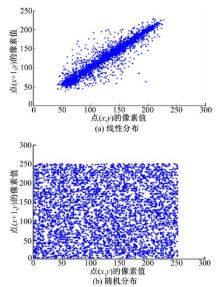
图7为垂直方向相邻像素相关性,图7(a)像素间相关性呈线性分布,而图7(b)像素间相关性呈随机分布,使得攻击者无法从相关性上破译图像。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 相邻像素的相关性Fig.7 Correlation between adjacent pixels

2.3.3 密钥敏感性分析

设定初始条件为E(0)=0.2和D(0)=0.2,图8是密钥为E(0)=0.20000000000001、D(0)=0.2时的解密图像,由图8可见,即便是微小的差别,都不能够正确解密,可知本文算法对密钥敏感。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 错误密钥解密图像Fig.8 Decryption image using incorrect keys

2.3.4 抗扰性分析

本文对原始图像添加了高斯噪声(均值为0,方差为0.02)、椒盐噪声(强度为0.02)和剪切攻击(像素从60~180范围的正方形),以验证算法的可靠性,如图9(a)(d)(g)所示。可以看到,图9(b)(e)(h)为加密图像,图9(c)(f)(i)为解密图像,从解密图像分析得知,图像有很好的抗噪能力,并且对剪切攻击有较好的抵御能力。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 抗扰性分析Fig.9 Anti-disturbance analysis