孟梦(1988),女,博士研究生.研究方向:交通规划与管理.E-mail:10114221@bjtu.edu.cn
首先运用超级网络理论构造适用于组合出行模式的交通超级网络。其次,在弹性需求的基础上,认为出行者出行模式及路径选择均具有随机性,给出广义费用下的路段费用函数表达式。运用交通平衡与变分不等式理论,分析弹性需求下组合出行模式的交通平衡条件,提出与平衡条件等价的变分不等式模型,并证明最优解的存在性与唯一性。最后,设计模型的求解算法,通过算例说明模型和算法的有效性,并分析参数变化对OD需求及模式划分的影响。算例结果表明:模型能够更真实地反映出行者的组合出行行为,具有一定的普适性。
A multi-modal traffic equilibrium model with combined modes is proposed. First, the super-network theory is applied to describe the traffic network with combined modes. Second, the mode and route choices are considered to be stochastic under elastic demand based on the generalized cost function. Using the network equilibrium theory, an equivalent variational inequality model is proposed after analyzing the network equilibrium conditions. Next, the existence and uniqueness of an optimal solution are given. Finally, a solution algorithm for solving the model is developed and validated by a numerical example. The influences of different parameters on Origin-Destination (OD) demand and modal split are analyzed. These results show that this model can reflect the combined travel behavior more practically and has certain generality.
近年来,一些专家学者注意到了组合出行模式下的交通流分配问题,提出了相关的模型与算法。Fernandez等[ 1]建立了固定需求均衡分配等价的数学规划模型。Wu和Lam[ 2]分析了步行和公交之间出行的换乘情况,利用变分不等式方法研究了弹性需求下的混合交通平衡分配问题。Lo等[ 3, 4]假定交通系统中存在私家车、公交车和地铁三种交通方式,基于Logit模型构建了组合出行模式下交通流分配模型,并进一步讨论了公交、地铁票价对交通流分布情况的影响。García和Marín[ 5]考虑了私家车和公交车混行时相互影响的不对称性,分别给出两种车的阻抗函数,并利用变分不等式建立了交通平衡模型。黄海军[ 6]和李志纯[ 7]针对小汽车和小汽车换地铁两种交通模式进行研究,分别给出了固定出行需求及弹性出行需求下组合出行模式的混合网络均衡条件,并提出了与平衡分配条件等价的变分不等式模型。吕能超等[ 8]考虑了停车换乘出行方式情况下出行者出行成本影响因素,分析了停车选择和路径选择的均衡条件,建立了等价的数学规划模型,算例结果说明合理的票价能够可控地、定量地转移流量。
上述研究存在如下不足:①对组合出行模式的交通网络结构特征分析不够全面,不能反映多种交通方式之间既相对独立又互相关联的特点;②大多假设出行者能够准确地掌握路网的交通阻抗,始终选择最短的出行路径,没有考虑出行者出行模式和路径选择的随机性。
针对上述问题,假定多方式交通网络中含有小汽车、自行车、公交和地铁四种交通方式,考虑组合出行模式下的随机交通平衡问题。组合出行模式下,出行者既要选择交通方式,还要同时选择出行路径。因此,本文是在弹性OD需求的前提下,研究有多少出行者选择单一出行模式和组合出行模式出行,以及交通量在路网上如何分布,建立满足随机平衡条件的变分不等式模型,给出模型求解算法,并通过算例说明模型和算法的有效性。
传统的交通网络是由许多节点和连接两个节点之间的边组成,节点代表道路交叉口、公交站点等,连接的边代表路段、公交线路等,这些边具有通行时间、通行费用和通行能力等多种属性。随着交通网络规模的不断扩大和结构的日益复杂,传统的单模式交通网络难以充分地描述组合出行模式下的交通网络特征,例如不同交通方式有各自独立的拓扑结构,各种交通方式子网络之间通过换乘行为相互关联,换乘时会存在换成费用、换乘时间及等待时间等多种属性。对此,可以引入“超级网络”[ 9]的概念,考虑组合出行模式的交通网络可以由一个包含多种交通方式子网的超级网络来表示。该超级网络具有网络嵌套网络,多层次、多级别、多属性的特征,子网络之间彼此独立又相互联系和影响,路段间的流量互不干扰。
考虑交通网络 G=( N, L), N为节点集, L为路段集。 O为起始节点集, O⊂ N, D为终讫节点集, D⊂ N; r为起始节点, r∈ O, s为终讫节点, s∈ D; M为出行模式集合, m为一种出行模式; I为交通方式集合, i为一种交通方式, i=1、2、3、4分别代表小汽车、自行车、公交和地铁; W为网络中OD对的集合, w为 W中的一个元素, w∈ W; P w为OD对 w之间的路径集合, p为其中的一条路径, 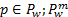
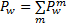
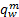
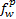
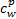
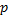
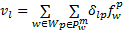
基于超级网络和扩展理论,将图1所示的普通路网转化为图2所示的超级交通网络。图2中实线表示行驶路段,点划线表示换乘路段,点线表示上下网路段。路段上的权值可以代表行驶时间、出行费用、舒适度等多种属性。
以往研究中,大多假设采用小汽车出行的用户遵循Wradrop第一平衡原理,选择费用最小的路径出行。但实际出行中,即使是配有ATIS装置,出行者也并不能完全了解路网全部信息,且路网中也会存在一些难以量化的因素,因此本文将路径阻抗视为一个随机变量,Wradrop第一平衡原理下出行者选择估计的最短路径出行,这就是随机平衡配流问题(Stochastic user equilibrium,SUE)。
在弹性需求下SUE建模中,任意OD对之间的出行需求量可表示为期望最小理解出行成本的单调下降函数[ 10],即
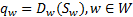 | (1) |
式中: S w为OD对 w间的最小期望出行费用,有
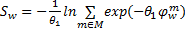 | (2) |
式中: θ1 为模型的校正参数,反映出行者对出行模式 m的费用感知误差程度; 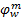
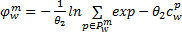 | (3) |
式中: θ2 为模型的校正参数,反映出行者对出行路径 p的费用感知误差程度。根据“树型”结构行为选择理论的要求[ 11], θ2≥ θ1>0。
假定路段费用相互独立,超级网络条件下路网中的路径费用可表示为各路段费用之和,即
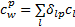 | (4) |
考虑组合出行的多方式交通网络路段包括行驶路段、换乘路段和上下网路段。为便于研究,本文将乘坐公交、地铁的票价和租赁自行车的费用转到上网路段或换乘路段上。假定路段的费用主要由出行时间、货币费用和舒适度三种因素构成,其中出行时间包括步行时间、行驶时间和等待时间。路段费用计算如式(5)所示:
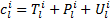 | (5) |
式中: 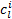
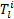
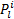
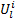
(1)小汽车
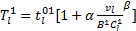 | (6) |
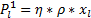 | (7) |
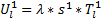 | (8) |
(2)自行车
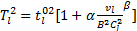 | (9) |
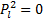 | (10) |
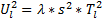 | (11) |
(3)公交车
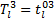 | (12) |
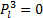 | (13) |
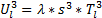 | (14) |
(4)地铁
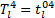 | (15) |
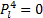 | (16) |
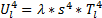 | (17) |
式中: 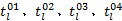
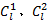
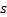
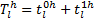 | (18) |
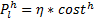 | (19) |
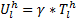 | (20) |
式中: 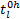
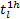
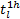
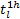
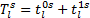 | (21) |
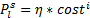 | (22) |
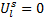 | (23) |
式中: 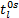
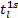
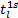
下网路段费用只包括路段上的步行时间: 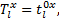
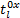
本文利用Logit模型来描述出行者对不同出行模式及路径选择的偏好。多方式交通网络达到随机平衡状态时,没有出行者能够通过单方面改变出行路径来减少最小期望出行费用,且出行模式与出行路径的选择均满足Logit型随机平衡,即式(24)(25):
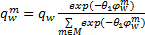 | (24) |
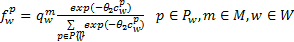 | (25) |
式(24)(25)分别反映出行者出行模式选择和路径选择偏好。网络OD需求量、路径流量满足如下约束条件:
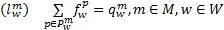 | (26) |
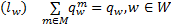 | (27) |
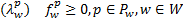 | (28) |
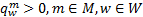 | (29) |
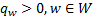 | (30) |
等式左侧括号中的字母表示的变量为对应的对偶变量。
构造变分不等式模型
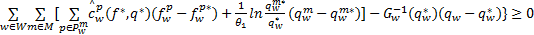 | (31) |
式中: 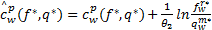
定理1 变分不等式模型式(31)等价于组合出行模式下多方式交通网络均衡条件式(24)(25),且满足需求条件式(1)。
证明 由变分不等式模型式(31)的KKT条件可得到:
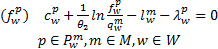 | (32) |
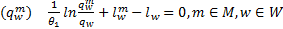 | (33) |
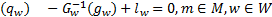 | (34) |
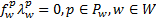 | (35) |
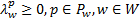 | (36) |
由式(32)有 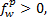
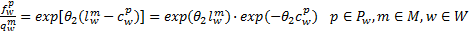 | (37) |
对 p求和,并结合守恒条件式(26),得:
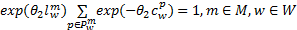 | (38) |
因此推出的 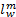
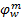
同理,可由式(27)和式(33)推出表示模式选择的Logit模型式(24),其中 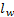
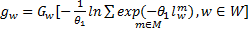 | (39) |
综上可以证明,变分不等式模型式(31)等价于组合出行模式下多方式交通网络均衡条件式(24)(25),且满足需求条件式(1)。证毕。
定理2 变分不等式模型式(31)至少存在一个解。
证明 由于变分不等式模型式(31)的可行域Ω={(26)-(30)}是一个由一系列的线性约束构成的集合,因此该可行域是紧的。同时,函数 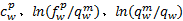
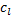
本文利用连续权重平均法(Method of successive weight average,MSWA)[ 12]求解模型。该方法与传统的迭代加权法(Method of successive average,MSA)的不同之处在于迭代步长不是一个固定值,而是随着迭代点接近最优解,将更多的权重分配给后迭代点,求解的收敛速度可以得到明显的提升。具体步骤表示如下:
Step1 初始化。置迭代次数n=0,令各路段流量 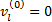
Step2 根据费用计算公式得到各个路段的费用 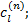
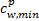
Step3 根据有效路径的判定条件,从遍历得到的路径中搜索出有效路径。判定条件为:换乘弧小于等于2条;路径费用 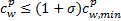
Step4 计算出行模式 m的最小期望费用 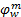
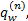
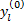
Step5 用MSWA法计算各路段当前交通量 
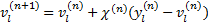 | (40) |
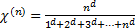 | (41) |
Step6 收敛检验。设 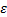
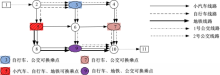
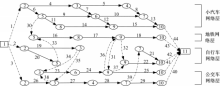
测试路网如图1所示,有一个OD对(1,11),四种交通方式(小汽车、自行车、地铁、公交),1条地铁线和2条公交线。OD对间存在六种出行模式, m= a、 b、 c、 d、 e、 f分别表示小汽车出行、公交车出行、小汽车换乘地铁出行、公交车换乘地铁出行、自行车换乘地铁出行、自行车换乘公交出行。构建得到的超级网络结构图如图2所示。模式 a和 b为单一出行模式,模式 c、 d、 e、 f为组合出行模式。
图2中,1、11分别表示起点和终点。弧段1-3为上网弧;弧段4-15为小汽车行驶弧;弧段16-18为地铁行驶弧;弧段19-22为自行车行驶弧;弧段23-29为公交行驶弧,其中23-25为公交1号线行驶弧,26-29为公交2号线行驶弧;弧段30-39为换乘弧;弧段40-44为下网弧。
OD需求函数采用负指数形式, 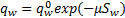
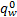
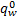
假定地铁各路段的行驶时间为3 min,发车间隔为4 min/辆;公交运行信息如表1所示,小汽车和自行车的出行信息如表2所示。
| 表1 公交运行信息 Table 1 Buses operative information |
| 表2 小汽车和自行车出行信息 Table 2 Bicycles and cares travel information |
计算结果表明:MSWA算法在44次迭代后,所求解达到了收敛要求。而同样精度,MSA算法需要迭代58次。比较两种算法可知,MSA算法在开始时收敛幅度较大,在接近解时收敛速度急剧下降,而MSWA算法的收敛速度明显提高。因此,在求解此类SUE模型时,MSWA算法较MSA算法收敛速度更快,且在一定迭代步数之后,计算精度更高。
表3列出了 θ2固定在0.5而 θ1变化时实现的OD需求比例及模式划分结果。表4列出了 θ1 固定在0.1而 θ2变化时实现的OD需求比例及模式划分结果。数据结果表明:①随着 θ1或 θ2的增大,OD对间的需求均减少。这是由于 θ1 或 θ2越大,表明出行者对路网信息的感知越准确,网络的不确定性越弱,因此出行者明智地做出是否出行的决策;②传统的Logit随机均衡分配模型为本文模型当 θ1= θ2 时的特殊情况。对比结果显示, θ1 比 θ2 对出行模式比例的影响程度更大,因此本文模型更能接近真实交通状态。此外,由于模型较传统模型增加了多个校正参数(如 θ1 、 θ2等),因此更适合多方式交通网络的出行费用敏感度分析。
| 表3 θ1变化时实现的OD需求比例及模式划分的结果 Table 3 Resultant OD demand and modal split for different θ1 % |
| 表4 θ2变化时实现的OD需求比例及模式划分的结果 Table 4 Resultant OD demand and modal split for different θ2 % |
表5列出了需求函数参数 μ的变化对OD需求分布及流量分布的影响结果。当 μ=1时,由于OD对间的出行阻力过大,导致OD对间的出行需求无法实现,有部分出行模式没有出行者出行。随着 μ的减少,出行者对出行费用的感知越小,越来越多的出行得到满足。当 μ =0时,OD对间实现的需求就是其潜在最大需求,表明此时OD对间的需求不受路网服务水平的影响。
| 表5 μ变化时的OD需求及流量分布结果 Table 5 OD demand and flow distribution under different μ |
(1)提出了多方式交通网络中的广义费用表达式,建立了考虑组合出行模式的SUE模型,所建模型更能贴近真实情况。
(2)利用MSWA算法求解模型,通过算例说明了模型和算法的有效性。验证了在求解此类问题时,MSWA算法的收敛速度明显优于MSA算法。
(3)算例结果表明:随着出行者对路网信息感知准确性的提高,网络的不确定性越弱,出行者越能明智地进行出行决策。随着出行者对出行费用的灵敏度的减小,出行者对出行费用的感知越小,越来越多的出行得到满足。当出行最大需求得到满足时,OD对间的需求不受路网服务水平的影响。
(4)本文的理论分析结果对于组合出行模式下的交通分配问题的建模,分析出行者的组合出行行为是非常有意义的,有望为最优公交线路的分布、公共交通票价的制定及换乘站点的布局与收费等问题提供一些思路。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|