靳文舟(1960),男,教授,博士生导师.研究方向:交通运输规划与管理.E-mail:ctwzhjin@scut.edu.cn
针对单条公交线路双向及单向客流分布的不均衡性,考虑我国大城市公交企业普遍依靠政府补贴,在实际运营中存在预算限制的情况,以社会总体效益最优为目标,建立了对区间车和双向全程车的发车频率及区间车折返位置同时进行优化的组合调度模型,探讨了预算限制对优化调度的影响,证明了预算限制相当于减少了乘客的时间价值,分析了预算限制下组合调度最优发车频率、折返点位置和系统成本的关系,并与单一调度进行对比。结果表明:在客流分布不均衡和预算限制的情况下,相比单一调度,组合调度能有效减少系统成本和乘客平均出行时间,节省运力,降低车辆拥挤,提高服务水平。在预算限制下,可以通过组合策略的实施,使出行乘客和运营企业都获益。
In order to solve the problem due to the unbalanced passenger demand, a single line transit mixed scheduling model for zonal vehicles is proposed. This model takes the factor into consideration that the bus companies generally rely on government subsidies and there exist financial constraints in big cities in China. With the target of maximizing the total social benefit, the model simultaneously optimizes the frequencies of zonal and full-length vehicles as well as turn-back point. The impact of financial constraints on transit optimization is explored, proving that financial constraints are equivalent to diminishing the value of passenger's time. Furthermore, a numerical example is present, and the relations among frequency, turn-back point, and cost under financial constraints are analyzed. Compared with the optimized single-line scheduling, the results indicate that mixed scheduling can save vehicles, the passenger travel time and the cost under unbalanced demand situation and financial constraints. The benefits for both operators and passengers can be obtained by reasonable allocation of vehicle operation form under financial constraints.
目前,对完全采用全程车的公交调度形式的研究相对成熟[ 1],而采用全程车、区间车和大站快车等多种调度形式的组合调度是当前公交优化的研究热点和难点。Vijayaraghavan[ 2, 3]探讨了基于大站快车和区间车调度策略下的车辆分配、组织和调度问题;Ceder[ 4]对采用大站快车或区间车策略下的公交调度模型进行了研究;根据线路双向客流的不均衡性,Furth[ 5]构建了考虑空车发出及中途载客等放车调度策略下的区间车调度优化模型;Eberlein[ 6]研究了公交运营控制中的越站问题。蒋光震[ 7]首次构建路线效率指标确定区间车的停靠站点,再根据线路乘客分布情况计算区间车和大站快车的均衡发车间隔;杨兆升[ 8]引入路段和客流集散量不均匀系数,从而给出确定区间车和大站快车途经站点的计算方法;徐大伟等[ 9]根据公交OD矩阵筛选大站快车站点,将原线路客流量分为大站快车和全程车两部分,再分别计算它们的均衡发车间隔;陈明明[ 10]探讨了不均衡发车间隔的全程车和区间车(大站快车)两种调度形式组合的公交组合调度问题;孙传娇等[ 11]考虑全程车、区间车和大站快车三种不同调度形式,建立了均衡发车间隔的公交组合调度优化模型,设计求解该问题的遗传算法,确定每辆车发车时刻和发车类型。然而,上述文献对于公交组合调度问题的研究大多数仅仅局限于对区间车折返点位置的合理选择[ 12, 13, 14, 15, 16],而且没有全面考虑线路上下行及单向客流分布的不均衡性,更未见探讨实际运营中预算限制对组合调度策略的影响。
针对单条公交线路单向及双向客流分布的不均衡性,考虑我国大城市公交企业普遍依靠政府补贴,在实际运营中存在预算限制,因此,结合我国国情,作者研究了预算限制下的公交车辆组合调度问题,以期为提高公交服务水平提供理论依据。
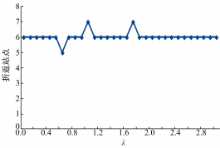
不失一般性,本文假设是一条双车场的双向公交线路,公交OD固定,客流出行分布主要集中在上行前半段和下行后半段,断面客流呈现如图1所示的类偏态分布,其中A表示全程车,车辆从线路起点站到终点站,必须在沿线各固定的车站依次停靠,并驶满全程的一种基本调度形式;B表示区间车,车辆仅行驶在从线路某一方向起点到折返点区段的一种辅助调度形式。公交线路在一个方向包含 N个站点( N-1个区间),如图2所示,运行方向(从1到 N)代表方向1(上行),相反方向(从 N到1)代表方向2(下行),区间车从起点1行驶到 s1并折返。 
本文提出了以下几个基本假设和定义:
(1)上车和下车过程同时进行,而且上车速率小于下车速率,故站点总停留时间主要取决于乘客上车总时间。
(2)车辆到达服从泊松分布或均匀分布。
(3)乘客均匀到达,并乘坐第一辆到达的车辆,因此,乘客平均等待时间在车辆到达服从均匀分布的情况下等于发车间隔的一半,在车辆到达服从泊松分布的情况下等于发车间隔[ 1]。
定义 乘客从 k站上车,在[ l1, l2]下车的人数(人/h): 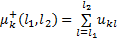
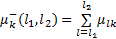
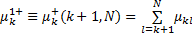

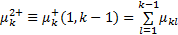
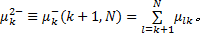
假设公交系统内采用一票制,企业的收入在OD已知情况下是固定的,经济效益好体现在运营成本的降低。公交系统成本包括乘客出行时间成本和公交公司运营成本。两者都会受到组合调度策略的影响,前者是因为乘客的等车时间和在车时间与发车频率和站点停靠站时间密切相关;后者是因为运力配置和线路满载率会随着组合调度策略的实施而变化。其中乘客出行时间成本包括等车时间成本和在车时间成本,而在车时间包括站点间运行时间及停靠站时间。
1.2.1 等车时间成本
组合调度下乘客等车时间成本取决于上(下)行方向区间车范围内和范围外的等车乘客需求 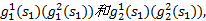
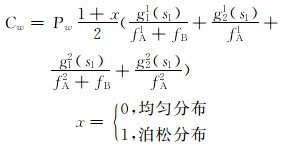 | (1) |
式中: 

1.2.2 在车时间成本
组合调度乘客在车时间成本主要取决于乘客在车行驶时间 g4以及上(下)行方向区间车范围内和范围外的乘客上车需求 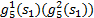
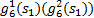
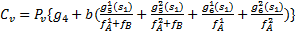 | (2) |
式中: P v表示在车时间价值; 
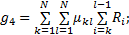
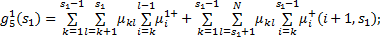
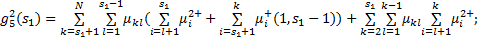
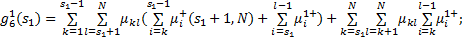
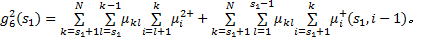
1.2.3 运营成本
根据文献[ 16],运营成本可分为时间成本和空间成本。前者包括司乘人员工资,而后者包含车辆运行成本,如燃油费、润滑油、轮胎磨损、维护费用等。单位时间运营成本可以表达为
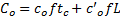 | (3) |
式中: c o表示每车小时费用(元/(veh·h)); c' o 
对于组合调度,运营费用包括全程车A的成本 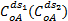
 | (4) |
式中:

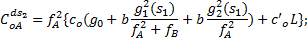
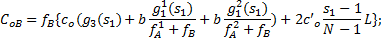


为了满足乘客乘坐第一辆到达的车辆的假设条件,车载容量必须能够容纳线路最高客流断面的所有乘客,基于固定公交OD分布,可以计算断面客流,进而根据发车频率可以求出车辆最高满载率,用来评价线路的拥挤程度和服务水平。最高满载率可表示为
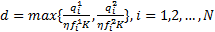 | (5) |
式中: 
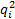


1.4.1 求解预算限制下组合调度问题的算法
由式(1)(2)(4)相加可得到组合调度模式下的系统总成本 
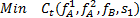 | (6) |
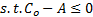 | (7) |
式(6)表示最小化公交系统总成本;式(7)表示组合调度的运营成本。 Co不超过预算限制 A 。
设 λ为不等式约束的乘数(本文称其为预算限制水平),根据拉格朗日乘子法则将其转化为如下无约束优化问题:
 | (8) |
根据一阶条件 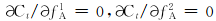
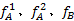
为了得到近似最优解,引入Furth提出的调度模式的概念[ 12],令 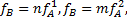

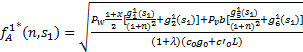 | (9) |
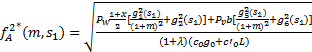 | (10) |
将式(9)(10)代入表示式 

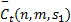
由于 Ct ( n, m, s1)中年 n、 m、 s1均为离散值,问题属于组合优化问题,对于给定的预算限制水平 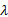
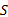
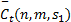

1.4.2 预算限制下单一调度的优化变量
当 f B =0即 m= n=0时,组合调度变为单一调度模型,于是可由式(9)(10)得到单一调度的优化变量为
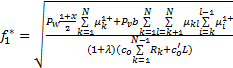 | (11) |
 | (12) |
1.4.3 关于预算限制的数理基础
在进行组合调度策略之前,给出如下定理。
定理1 预算限制水平 λ随着预算 A的减少而增大。
证明 假设有如下凸规划问题:
 | (13) |
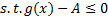 | (14) |
如果 λ是约束条件的乘数,根据拉格朗日乘子法则,问题转化为
 | (15) |
即
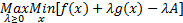 | (16) |
因为 λ A与 x无关,于是可以得到最优的 x * ( λ )满足
 | (17) |
最后,问题可以转化为
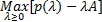 | (18) |
令 λ i为 λ预算限制 A i的约束因子,则
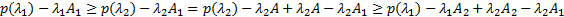 | (19) |
由式(17)可以得到
 | (20) |
因此,乘数 λ随着预算 A的减少而增大。证毕。
定理2 预算限制在优化调度中相当于减少乘客的时间价值。
证明 从最优发车频率式(9)可得:
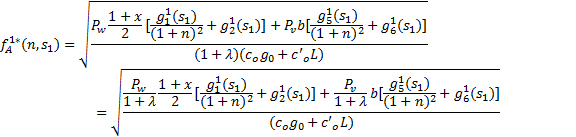
从上式可以看出:预算限制将乘客等车时间价值 P w和时间价值 P v分别减少为 P w/(1+ λ)和 P v/(1+ λ)而且预算限制水平 λ越大,乘客时间价值越小。
与式(9)类似,从式(10)(11)(12)也可以得到上述结论。因此,预算限制在优化调度中相当于减少乘客的时间价值。证毕。
假设某条公交线路有10个站点,OD分布矩阵和断面客流如表1和图1所示,断面客流呈现明显的偏态分布,客流出行主要集中在上行方向的前半段(1→5)。参数假定如下: L=8 km, P w=30 元/h, P v=20 元/h, c o=20 元/(veh·h), c' o=10 元/(veh·km), b=5 s/人, K=60 人/veh, K=60 人/veh, η=0.9。
| 表1 公交OD矩阵 Table 1 OD matrix of bus |
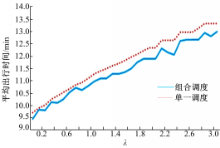
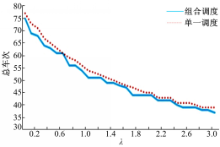
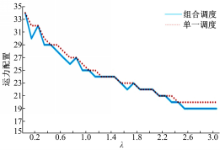
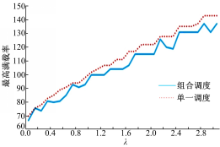
由图3、图4可以看出:随着预算限制水平 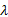
在图3(c)中,运营成本与预算限制水平 λ一一对应,运营成本随着 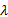
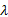
从表2可以看出:在相同的预算限制水平 λ时,组合调度比单一调度的运营成本有所减少,但相差不大,乘客等车时间成本、在车时间成本和系统总成本分别减少2.2%、1.26%和1.32%,运力配置从28台减少到27台,车辆最高满载率从91%减少到85%,因此,在减少企业成本的同时也提高了服务水平,与上述结论一致。
| 表2 当预算限制 λ=0 .6时的优化变量 Table 2 Optimal values for financial constraints λ=0.6 |
图8和图9分别给出了在不同预算限制水平下组合调度与单一调度的最优发车频率以及组合调度最佳折返站点。从图8可以看出: 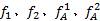
(1)预算限制会导致乘客出行时间及其成本和系统总成本增加,同时减少公交资源供给,导致最高满载率的增加和服务水平的下降。
(2)在客流分布不均衡和预算限制的情况下,相比单一调度,组合调度能有效减少乘客出行时间及其成本和系统总成本,同时可以节省运力,降低车辆拥挤程度,提高服务水平。
(3)预算限制会影响组合调度最优折返站点的选取。
(4)本文方法是基于固定需求和单条公交线路,后续的研究工作可考虑弹性需求下的情形,并且将单条公交线路进一步扩展到公交网络。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|