詹伟(1983),男,博士研究生.研究方向:交通流与交通安全分析.E-mail:zhanwei@zju.edu.cn
在典型高速公路隧道群路段交通事故调查的原始数据基础上,建立事故灰色预测模型,并利用残差模型对其修正,分析隧道群路段交通事故发展变化趋势。通过引入马尔可夫模型进行优化,提高预测精度。与目前常规交通事故预测方法相比,本文方法在一定时段内具有更好的预测精度和实用性,可为高速公路隧道群路段交通事故预测分析及交通安全预警提供参考。
Based on the original data of traffic accidents in a typical highway tunnel group region, a grey forecasting model, which is modified by residual error model, is proposed to analyze the development trend of traffic accidents in highway tunnel group region. The forecasting accuracy is improved by introducing Markov optimization. Compared with commonly used forecasting method, the proposed method in this paper has a better forecasting accuracy and practicality in a period. It can be used for the forecasting analysis of traffic accidents and for security early warning in highway tunnel group region.
受环境条件限制,山区高速公路往往线路复杂,高边坡、长下坡、高架桥、隧道群等特殊路段集中,对交通安全不利。特别是隧道群路段交通环境复杂,行车条件差,通行能力下降,在大交通流量下,产生的交通安全问题十分突出。
影响隧道群路段行车安全的因素众多且作用机制复杂。隧道群路段的交通事故,一方面与道路条件、交通设施完善程度、视距及照明条件等确定性因素有关,另一方面又受交通量大小、驾驶员心理状态、气候变化等不确定性因素影响。目前,上述因素对交通事故发生的作用机制尚不明确。张生瑞等[ 1]结合隧道出入口处和隧道内的通风、照明和道路特征对交通的影响进行了交通事故多发段的成因分析;张玉春等[ 2]将隧道群交通事故风险划分为不同阶段,认为不同阶段的风险值随人的因素、车辆因素、隧道群环境因素和防灾救援力大小而改变。
本文在甬台温高速公路猫狸岭隧道群路段交通事故调查分析的基础上,运用灰色理论建立隧道群交通事故预测模型,在此基础上引入马尔可夫模型进行优化,提高预测精度。本文的方法可用于分析不同交通条件下隧道群路段的交通事故变化趋势,为高速公路相关路段交通安全预警及制定相应事故预防对策提供依据。
山区高速公路隧道群由于其呈隐蔽带状的分布特点,给交通行车环境带来了一系列的变化,交通安全问题十分严重。特别是大交通流量路段的长大隧道群区域,往往成为高速公路交通事故高发区。
本文分析了浙江省甬台温高速(宁波-台州-温州)、金丽温高速(金华-丽水-温州)、甬金高速(宁波-金华)、上三高速(上虞-三门)、杭金衢高速(杭州-金华-衢州)五条高速公路隧道及隧道群区域的交通事故资料。如图1所示,五条高速公路隧道路段总长81.69 km,占公路总长的6.7%,而隧道区域事故比例超过五条公路事故总数的10%。由对比(图1)可见,五条公路中,除甬金高速因交通流量小,隧道路段事故率略低于一般路段,其余四条高速公路隧道路段的事故率均高于一般路段事故率,其比值为1.20~1.95,其中,甬台温高速隧道区的事故率接近一般路段的2倍。
 | 图1 山区高速公路隧道路段与一般路段事故率对比Fig.1 Accident rate comparison of tunnel group region and general section in mountainous highway |
以典型的事故高发路段甬台温高速猫狸岭隧道群为例。该隧道群位于上三高速和甬台温高速交汇处,由四座长短不一的隧道组成,隧道总长超过5.2 km,分布于8.2 km长的路段上,隧道路段占该路段总长的64%。该路段按双向四车道设计,目前单向日交通量超过1.8万辆,高峰时段车流已经接近饱和状态。由于交通流量大,交通环境复杂,该路段时常因事故而发生交通拥堵,给交通安全和畅通运营造成了严重影响。
图2对比分析了该路段车流量与事故数量的关系,由图可见,当年车流量增长1倍(即从2002年的532万辆增加到2007年的1037万辆),年事故数同比增长了近3倍,年百万车辆事故率由11起增加到23起,事故率明显高于一般路段的平均水平。
 | 图2 猫狸岭隧道群车流量及事故数对比Fig.2 Comparison of vehicle flow and number of accidents in Maoliling tunnel group |
与一般路段相比,隧道群区域的事故对高速公路交通安全的危害和影响更大。高速公路隧道群区域的封闭设计和平行公路网的缺失,使得高速公路隧道群区域的事故具有影响范围广、易造成大范围交通堵塞、救援和疏散困难、对周边环境具有“连锁反应”和“灾害辐射放大效应”等特点。这些区域一旦发生重大的事故,后果非常严重,处理不当或不及时将造成高速公路交通运输网的区域性瘫痪,并可能给人员和公共财产带来损失,造成广泛的社会影响。在目前难以从根本上解决隧道群区安全事故多发问题前,从安全管理入手进行事故预测分析,提高管理水平,做好应对隧道群路段交通事故的预案就显得十分重要。
由于交通事故数据具有不完备性,信息具有模糊性,因此事故资料既不是规律明显的白系列数据,也不是毫无规律的黑系列数据,而是一个灰色系列数据,用灰色预测模型进行分析可较好地反映数据的实际特点[ 3, 4]。
在使用灰色系统理论建立交通事故预测模型时,先采用累加生成的方法对时间数据列进行处理,弱化数据的随机性,将其转化为较有规律的数据。通过累加可以得出数据积累过程的发展趋势,显现出离散数据中隐含的积分特性或规律性[ 5]。如给定数据列:
[x(0)(ti)]=[x(0)(t1),x(0)(t2),…,x(0)(tn)] (1)
式中:x(0)为原始数据序列;t为时间因子。
显然式(1)中的数据列通常都是规律不明显的时间序列,需要作数据累加生成处理,令
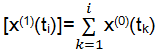 | (2) |
得到新的数据列:
[x(1)(ti)]=[x(1)(t1),x(1)(t2),…,x(1)(tn)] (3)
经过累加处理后得到的新数据列随机性被弱化,呈现明显的规律性增长趋势,可根据需要进行n次累加处理,直至满足要求。这里建立灰色动态模型GM(1,1),其微分方程为
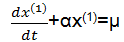 | (4) |
式中:x(1)为原始数据x(0)(ti)经过累加生成处理得到的新数据列;α、μ分别为建模过程中待辨识的参数和内部变量,可由最小二乘法计算求得:
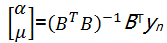 | (5) |
 | (6) |
 | (7) |
求解微分方程(4),可以得到相应的时间函数:
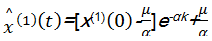 | (8) |
从而得到数据还原模型:
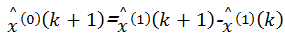 | (9) |
由式(9)得到的预测结果 x(0) 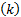
 | (10) |
式中: x(1)( k)为实际原始数据累加值; 
对残差数据列进行累加生成处理:
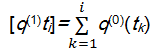 | (11) |
[ q(1)( t i)] =[ q(1)( t1), q(1)( t2),…] (12)
一般进行两次累加生成处理就可获得满意的结果。继续灰色预测模型中的参数识别过程,将 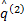
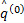
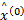
采用后验差检验上述数据残差模型修正得到的预测值精度是否满足要求。设原始数列 X与残差数列 E的平均值分别为 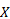

 | (13) |
 | (14) |
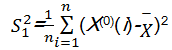 | (15) |
 | (16) |
定义后验差比值 C及小误差频率 M分别为
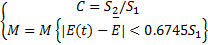 | (17) |
外推性好的预测, C值必须小,一般要求 C<0 .35,最大不超过0 .65;而 M值必须大,一般要求 M>0 .95,不得小于0 .7。
按 M与 C的大小,可以将预测精度分为4个等级,如表1所示。
| 表1 M、 C值预测精度表 Table 1 Forecasting accuracy class of M, C |
利用上述灰色预测模型对高速公路隧道群路段交通事故进行预测,虽然可以较好地反映出隧道群路段交通事故在未来一段时间内的发展趋势,但是该模型是通过累加处理得到的,使得原始数据的随机性弱化,不适合长期随机性和波动性大的数据序列预测,而且隧道群路段不同于一般路段,事故的发生是系统中多种因素综合作用的结果,包括确定因素和不确定因素的影响。这些因素对交通事故发生的作用机理本身就非常复杂,导致交通事故成为具有很强的偶然性、不确定性和模糊性的随机事件。因此灰色模型对于这类随机波动性较大的事故数据序列的预测精度较低。
马尔可夫随机过程理论可弥补灰色模型的局限性,它通过确定状态的转移规律来反映事件的随机波动性影响[ 6, 7],二者结合可以使预测模型得到优化,灰色模型得到的数据序列满足了马尔可夫随机过程理论的前提条件,即无后效性和平稳等均值的特点,引入马尔可夫模型可以确定状态的转移规律,从而提高预测精度[ 8, 9, 10]。
(1)状态划分
建立马尔可夫模型的关键是要了解状态的转移规律。为了构造状态转移概率矩阵,首先要将原始数据序列划分成若干子序列,根据数据序列的特点,可以把用上述灰色模型得到的预测值与实际值的差值划分为若干状态,分别记为R1,R2,…,Rn。状态划分的数量与样本数以及拟合数据的误差范围有关,一般可划分为3~5个状态。
(2)状态转移概率矩阵计算
状态转移概率可以由式(18)得到:
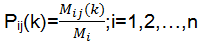 | (18) |
式中:Mij(k)为由状态Ri经过k步转移到状态Rj的原始交通事故数据样本数;Mi为处于状态Ri的原始交通事故数据样本数;Pij(k)为由状态Ri经过k步转移到状态Rj的概率。
得到状态转移概率矩阵:
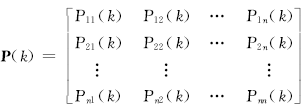 | (19) |
状态转移概率矩阵反映了系统各状态转移的统计规律,一般只要考察一步转移概率矩阵 P(1)。通常可以采用比较法预测下一步状态,即以最大概率所处状态作为未来的发展状态,该状态所对应区间的中间值作为最终预测结果。
本节根据猫狸岭隧道群路段2002年至2007年的交通事故资料,利用交通事故灰色预测模型对该路段未来几年交通事故次数进行预测。原始交通事故数据见表2。
| 表2 猫狸岭隧道群2002~2007年交通事故总次数 Table 2 Number of traffic accidents of tunnel group region in 2002~2007 |
首先根据原始数据建立灰色预测模型,相关参数见表3。
| 表3 事故数据列累加生成处理结果 Table 3 Accumulated generating result of data column |
y n =[0 .85,1 .65,1 .42,1 .81,2 .26]T (20)
 | (21) |
利用式(5),可以计算得到 α=-0 .1856, μ=0 .8622。
令 x(1)(0)= x(0)(0)=0 .60, k=0,将 α、 μ代入式(8),可得时间响应函数: 
| 表4 残差数据列 Table 4 Residual data column |
将第二次累加值q(2)(k)代入式(5),可以计算出α=0.1362,μ=-0.1688。从而得到时间响应函数:
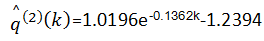 | (23) |
对时间响应函数进行残差检验和后验差检验,其结果为方差比C=0.189<0.35,小误差概率M=1>0.95。说明所构建的交通事故灰色预测模型精度良好,可以较好地反映出隧道群路段交通事故的发展变化趋势。从而可以得到该隧道群路段2003~2007年的预测值和差值,见表5。
| 表5 灰色预测值和差值序列 Table 5 Grey predictive value and differential value column |
从表5中可以看出,灰色预测值与实际值的差值序列的变化范围为[-22,36],由于样本数据有限,可以将数据划分为3个状态,分别为R1:[-22,-15],R2:[-15,-1],R3:[-1,36]。从而可以得到隧道群交通事故一步状态转移概率矩阵:
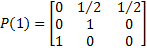 | (24) |
2007年交通事故数处于状态 R2,根据状态转移矩阵,采用比较法,可以预测2008年事故数量状态处于 R2,即2008年事故数量预测差值变化落在 R2:[ -15, -1]中,取其区间中位数 -7作为2008年事故数量灰色预测值与实际值的差值,可以在灰色预测的基础上确定2008年的预测值。
同理预测2009年的事故数量状态,可以采用滑动转移概率,去掉状态序列的第一个值,即2003年的状态值,加入2008年的预测状态值,得到新的状态转移概率矩阵,预测结果见表6,可以看出,经过马尔可夫随机过程优化后的预测结果精度得到了提高。
| 表6 隧道群路段2008~2009年事故预测结果 Table 6 Accidents forecasting in 2008~2009 in tunnel group region |
(1)高速公路隧道群路段事故率明显高于一般路段,这与隧道群特殊环境、交通设施等确定性因素有关,同时又受一些不确定因素如交通流量变化、驾驶员心理状态、天气及气候异常等的影响。
(2)在调查分析典型高速公路隧道群路段交通事故原始数据的基础上,运用灰色理论建立预测模型,并利用残差模型进行修正,分析隧道群路段交通事故发展变化趋势,在此基础上引入马尔可夫优化,使得预测精度得到提高。
(3)通过建立隧道群事故灰色预测模型并进行马尔可夫优化,使得高速公路隧道群交通事故预测在一定时段内具有较好的精度和实用性,可为高速公路隧道群路段交通事故预警和安全控制提供有效的决策支持。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|


