钟春玲(1973),女,教授,博士.研究方向:结构工程.E-mail:zhongchunling11@sina.com
为了准确计算连续配筋混凝土路面在温度作用下整个路段任意点的位移和应力,基于钢筋混凝土间粘结滑移效应,考虑地基摩阻力的影响,采用接触有限元理论形成了连续配筋混凝土路面的刚度方程,建立了考虑各个裂缝间隔段和锚固地梁之间联合作用的整个路段各部分应力和位移的理论分析模型。基于理论模型,探讨了连续配筋混凝土路面在温度应力作用下的钢筋与混凝土各部分的位移和应变的分布规律。对整个路段的数值模拟分析结果表明了方法的有效性和可行性。
In order to accurately calculate the displacement and the stress of any point on the Continuously Reinforced Concrete Pavement (CRCP) under thermal stress, the stiffness equation of the CRCP is established using the contact element theory. This equation is based on the bond-slip relation between reinforced steel bar and concrete, and the subgrade friction effect is taken into consideration. The finite element solution of the stress and displacement along the whole pavement is obtained by considering the combined action of crack interval and beams-on-foundation. Based on the theoretical model, the distribution rule of the stress and displacement of the steel and concrete in the CRCP under thermal stress is analyzed. The numerical simulation results of the whole pavement validate the feasibility of the proposed method.
连续配筋混凝土路面(CRCP)是在路面纵向配置连续的钢筋,中间不设横向胀缩缝,与普通混凝土路面相比,其耐久性和整体性以及行车舒适性都较好,而且CRCP的养护维修费用小,在欧洲和美国被广泛采用[ 1, 2]。在CRCP的设计计算过程中,冬夏温差产生的路面变形受到地基及连续钢筋的约束,所以CRCP的温度应力是造成路面破坏的主要因素[ 3, 4],它往往超过荷载应力成为路面设计的主要控制指标。
国内外学者对CRCP的温度效应进行了研究,形成了设计规范,并给出了该类路面的设计指标[ 5, 6]。设计规范存在一定的局限性,例如我国的设计规范不能考虑裂缝宽度等因素的影响,而AASHTO设计方法则是基于观测数据得出的经验公式。
对CRCP开裂情况的研究,国外学者主要采用现场观测和加速加载试验的方法[ 7, 8],缺乏深入的理论分析。同样我国学者也对CRCP的裂缝发展情况进行了现场观测[ 9]。在理论分析方面,国内学者典型的研究成果为以两条相邻裂缝之间的路段为研究对象,假定裂缝处钢筋的位移为零,推导了CRCP在季节性温差作用下受力性能[ 10, 11]。然而在实际工程中,裂缝处钢筋的位移并不为零,使得各裂缝间隔段存在耦合,从而导致现有的理论求解模型在端部区域存在较大误差。
为了解决上述问题,基于有限元方法的基本理论,建立了连续配筋混凝土路面力学行为的温度效应分析模型。该理论模型最大的特点是能够考虑裂缝处钢筋的实际位移当作约束条件,从而考虑各裂缝间隔段的耦合效应。此特点决定了用本文的理论分析模型可以精确计算出温度作用下连续配筋混凝土路面整个路段各区段的静力响应。
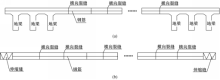
如图1所示,CRCP通常在端部设置锚固地梁来约束由于混凝土干缩和温度变化引起的路面位移(见图1(a))。也可以通过计算在端部设置桥梁用伸缩缝的方式满足端部位移(见图1(b))。因为在连续配筋混凝土路面中,钢筋是等间距布置的,根据弹性力学基本原理可取出任意含一根钢筋、宽度为一个钢筋间距的板条进行分析。基本假定如下:①钢筋和混凝土之间的粘结应力与两者之间的位移差成正比;②地基摩阻应力与混凝土路面板的位移成正比;③假设混凝土路面板与地基始终不脱离[ 5]。
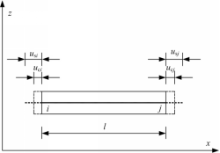
单元模型如图2所示,路面在温度应力作用下的位移包括混凝土路面板的轴向位移u c(x),钢筋的轴向位移u s(x)。混凝土路面板与连续钢筋的粘结应力系数为k s,地基摩阻力系数为k c。
1.2.1 单元的位移模式
在连续配筋混凝土路面中,钢筋位于路面的中性层位置,先给出钢筋的位移模式对结构分析的影响,令钢筋的纵向位移为
u s( x) =a1+a2x+a3x2+a4x3 (1)
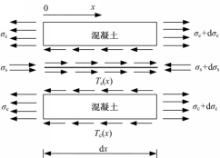
如图3所示,根据微元体的受力平衡关系可得:
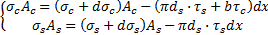 | (2) |
式中:A s为钢筋的横断面面积;A c为混凝土板的截面积;d s为钢筋直径;b为混凝土路面板的宽度;σ s为钢筋应力;σ c为混凝土应力;τ s为钢筋与混凝土之间的粘结应力;τ c为混凝土路面板与地基之间的摩阻应力。
由式(2)可知:
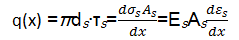 | (3) |
式中:ε s为钢筋的应变;E s为钢筋的弹性模量;E c为混凝土的弹性模量。
由材料力学可知:
ε s=u' s (4)
所以
q(x) =E sA su″ s(x) (5)
由基本假定可知:
τ s=k s·Δu(x) (6)
式中:
Δu(x) =u s(x) -u c(x) (7)
根据式(1)(3)(5)(6)可得:
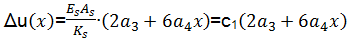 | (8) |
式中:c1=(E sA s)/K s,K s=k s·∑ πd s。
由式(1)(7)(8)可得:
u c(x) =a1-2c1a3+(a2-6c1a4) x+a3x2+a4x3(9)
将一个单元划分为两个节点(i,j),每个节点对包括混凝土位移和钢筋位移两个自由度,所以每个单元包括4个自由度,即u si、u ci、u sj、u cj。因此单元内各部分的位移在节点位置处可以写成如下形式:
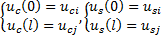 | (10) |
将式(10)代入式(1)和式(9)可得
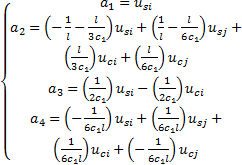 | (11) |
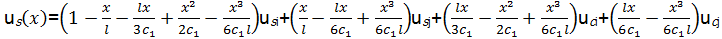 | (12) |
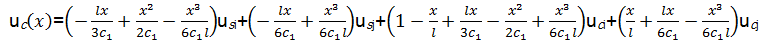 | (13) |
写成矩阵形式为
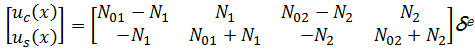 | (14) |
式中:
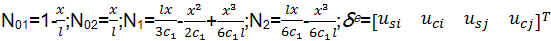
1 .2 .2 单元的几何方程
令混凝土路面板和连续钢筋的应变分别为 εc 
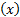
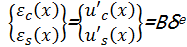 | (15) |
式中: B为应变矩阵:

根据式(7)(8)可知连续钢筋与混凝土路面板之间的滑移量为
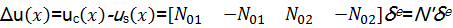 | (16) |
1.2.3 单元的物理方程
(1)应力与应变的关系
根据弹性力学的基本原理,路面单元的节点力列阵可表示为
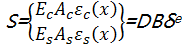 | (17) |
式中: D = 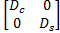
(2)钢筋与混凝土之间的粘结力与滑移量之间的关系
τs(ξ)= ks Δu (ξ) = N ' δ e (18)
(3)混凝土的位移与地基摩阻力之间的关系
假定在一个单元内地基摩阻力与混凝土路面的位移之间的关系为线性,则地基应力为
τc(x) =kc uc(x) =kc N ″ δ e (19)
式中:
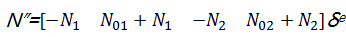
1 .2 .4 单元的刚度方程
设单元结点力列阵为
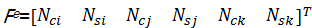 | (20) |
则单元的总势能为
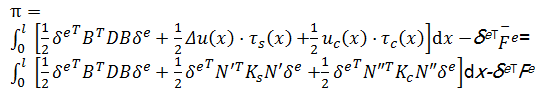
式中:Kc =kc b。
根据最小势能原理,对系统的势能函数 π取一阶变分,并令 π的一阶变分为零:
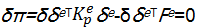 | (22) |
由式(22)可得到路面部分的单元刚度方程为
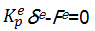 | (23) |
式中: 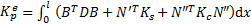
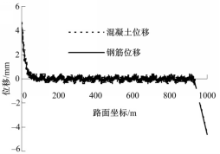
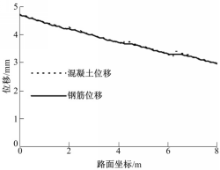
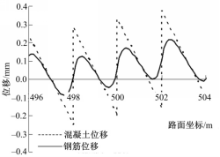
利用上述公式,分析了降温30 ℃时(假设施工温度为10 ℃,统计资料表明长春地区月平均最低气温为 -20 ℃),图4为一条1000 m长的 CRCP的位移和应力状态,其中板厚为25 cm,钢筋间距为10 cm,d s =14 mm,钢筋和混凝土的线膨胀系数α =1 .0 ×10 -5,k c =4 kPa/mm,E c =3 .25 ×107 kPa,E s =2 .1 ×108 kPa,k s =50 ×103 kPa/mm。 CRCP中钢筋和混凝土的位移计算结果如图5 ~图7所示。
图5给出的是全路段钢筋和混凝土路面板的位移状态,图6给出的是路段坐标0~8 m范围内的钢筋和混凝土路面板的位移状态,图7给出的是路段坐标496~504 m范围内的钢筋和混凝土路面板的位移状态。根据图4给出的裂缝分布情况,可知路段在坐标为2 m、4.25 m、6.25 m处均存在裂缝,从图6中可以看出,裂缝处的钢筋位移不等于零,图7中混凝土位移有突变的位置即为裂缝存在的位置。从图6和图7中可以,看出在降温作用下CRCP的钢筋位移不等于零,但是在路面的中段区域裂缝处的钢筋位移较小。因此当端部设置的桥梁用伸缩缝时,应采用全路段联合分析CRCP的位移和应力状态。
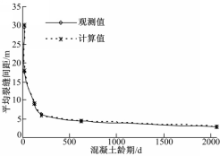
为了说明上述计算理论的合理性,利用本文推导的计算理论结合裂缝发展规律得到的裂缝平均间距和文献[9]中的观测结果进行了对比分析,如图8所示,
可以看出二者吻合得较好,说明利用本文的分析方法能够较为精确地计算连续配筋混凝土路面在温度作用下的位移状态。
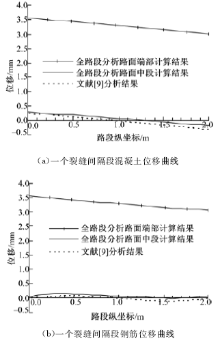
目前对CRCP位移的计算大多采用文献[ 11]给出的计算理论,该理论是取一个裂缝间隔段单独分析,以裂缝处的钢筋位移为零作为前提进行计算,由于忽略了各个裂缝间隔段的相互作用,会给计算结果带来一定的误差,本文计算理论考虑了路面全长内所有裂缝间隔段的联合作用,更符合实际受力情况。二者的计算结果如图9所示,可以看出:以某路段端部计算出的钢筋和混凝土位移,均与以该路段中部计算出的相应位移存在一定差异,混凝土的位移最大相差20%左右, 在道路的端部区域差别较大,说明本文给出的计算结果有较高的应用价值。
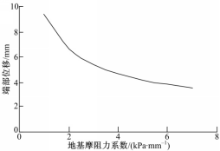
对于两端设置伸缩缝的CRCP,其端部位移的计算是控制伸缩缝设置类型的关键,因此本文给出了不同地基摩阻力系数对端部位移的影响,如图10所示。从图10可以看出,地基摩阻力系数越大,端部位移越小,说明地基对路面板的约束越强,从控制端部位移的角度分析,地基摩阻力系数越大对结构越有利。
基于有限元方法,建立了连续配筋混凝土路面力学行为的温度效应分析模型。该模型最大的特点是能够考虑裂缝处钢筋位移的实际状态,从而考虑各裂缝间隔段的耦合效应。采用数值模拟方法计算了温度作用下连续配筋混凝土路面整个路段各区段的静力响应,并与现有的计算理论进行了对比分析。结果表明本文给出的计算理论有较高的推广应用价值。最后给出了设置伸缩缝的连续配筋混凝土路面端部位移与地基摩阻力系数的对应关系,为设置伸缩缝的允许宽度提供了理论依据。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|