引用本文
王聪, 郭乃胜, 赵颖华, 谭忆秋. 不同成型方法和级配的沥青混合料内部空隙特征. 2014, 44(1): 74-80
WANG Cong, GUO Nai-sheng, ZHAO Ying-hua, TAN Yi-qiu. Air voids distribution of asphalt mixtures in different compaction methods and aggregate gradations. 吉林大学学报(工学版), 2014, 44(1): 74-80  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
不同成型方法和级配的沥青混合料内部空隙特征
王聪1,2, 郭乃胜1,2, 赵颖华1,2, 谭忆秋3
1.大连海事大学 道路与桥梁工程研究所,辽宁 大连116026
2.辽宁省公路工程重点实验室,辽宁 大连 116026
3.哈尔滨工业大学 交通科学与工程学院,哈尔滨 150090

王聪(1987),男,博士研究生.研究方向:道路工程.E-mail:lnwangcong@163.com

基金:“十一五”国家科技支撑计划项目(2008BAG10B02); 高等学校博士学科点专项科研基金项目(20092125120005); 中央高校基本科研业务费专项项目(2011QN136,2012TD015);
摘要

采用X-ray CT技术和数字图像处理技术研究两种成型条件下三种级配沥青混合料试件的内部空隙特征,并通过统计分析提出数学模型对其进行表征。结果表明,沥青混合料的空隙空间分布规律受试件成型方法及级配类型的影响较大。不同级配条件下,马歇尔试件内部空隙率分布沿着高度方向总体呈现对称形状,而静压试件内部空隙率分布则为“一端大,一端小”的形状,马歇尔试件的平均空隙率与目标空隙率差异较小,而静压试件的平均空隙率是目标空隙率的1.4倍以上;相同级配条件下,与马歇尔试件相比,静压试件的空隙空间分布离散性、平均空隙率和平均空隙数量均较大,但平均空隙等效直径相差较小;采用两参数数学模型能够较好地表征成型方法和集料级配对沥青混合料内部空隙空间分布规律的影响。

关键词: 道路工程; 沥青混合料; 空隙; X-ray CT; 成型方法
中图分类号:U414.103 文献标志码:A 文章编号:1671-5497(2014)01-0074-07
Air voids distribution of asphalt mixtures in different compaction methods and aggregate gradations
WANG Cong1,2, GUO Nai-sheng1,2, ZHAO Ying-hua1,2, TAN Yi-qiu3
1.Institute of Road and Bridge Engineering, Dalian Maritime University, Dalian 116026, China
2.Key Laboratory of Highway Engineering of Liaoning Province, Dalian 116026, China
3.School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150090, China
Fund:
Abstract

The air voids distribution of three gradations of aggregate is characterized using X-ray computed technology and digital image processing technology. Furthermore, a mathematic model is proposed to describe the air void distribution inside the asphalt mixtures by means of statistical analysis. The results show that both the gradations of aggregate and compaction methods have considerable influence on the air voids distribution within the specimens. Results also show that the voids distribution is symmetric along the depth of the Marshall specimens, whereby, the air voids distribution in the statically compacted specimens in nonsymmetrical along the depth that the number of air voids on the top part of the specimen is bigger than that at the bottom part. There is little difference between the target void fraction and the mean void fraction of the Marshall specimens; while the mean void fraction of the static compaction specimens is over 1.4 times of the target void fraction. In comparison with the Marshall specimens in uniform gradation of aggregate, in the statically compacted specimens, the number of air voids is bigger and the fluctuation along the depth is more remarkable, but the void size is almost consistent. Sstatistical analysis validates the applicability of the two parameter mathematical model to characterize air void distribution in asphalt mixture, and to quantify the effects of compaction methods and gradation of aggregate on air voids.

Keyword: road engineering; asphalt mixture; air voids; X-ray CT; compaction method
0 引言

从20世纪90年代开始,应用数字图像处理技术,特别是计算机层析识别技术(X-ray CT技术,简称CT技术)分析沥青混合料内部结构的研究相继开展。利用CT技术进行沥青混合料的细观研究主要集中于沥青混合料的内部结构特征识别、基于CT技术的沥青混合料数值模型重构及力学行为分析。Masad等[ 1, 2]采用CT技术分析SGC成型试件与现场压实取芯试件的内部结构特征,利用Weibull分布描述不同压实功的SGC试件内部空隙率和等效直径分布规律。Wang等[ 3]利用CT技术对Westrack试验路取芯试件的空隙分布进行分析,并提出沥青混合料三维重构的方法。You[ 4]基于CT技术获取沥青混合料的内部结构特征,采用离散元方法建立沥青混合料数值模型,据此实现劲度模量的黏弹性数值模拟。Arambula等[ 5]采用CT技术对不同压实度的SGC试件的空隙分布和连通性进行分析,评价了沥青混合料的空隙分布和水稳性的关系。裴建中等[ 6]和李芬等[ 7]均采用分形理论和CT技术相结合的方法对沥青混合料内部结构复杂程度进行了量化研究,并分析了沥青混合料内部的集料、沥青和空隙分布特征及其对沥青混合料路用性能的影响。汪海年等[ 8]阐述了利用CT技术研究沥青混合料的细观特征,以及CT技术对动态加载的同步识别和数值试验的重要意义。李晓军[ 9]利用CT技术对SGC试件的内部损伤行为进行了识别和仿真研究,并取得了较为满意的效果。但对沥青混合料的内部空隙特征研究,主要基于国外规范建议的成型方法或级配类型,因此研究成果具有一定的局限性,特别是在我国现行规程下,不同级配沥青混合料的空隙空间分布规律以及试件成型方法对其的影响情况尚待进一步研究。

本文根据我国现行的两种试件成型方法,以三种级配类型的沥青混合料试件作为研究载体,基于CT技术与图像处理技术对沥青混合料内部的空隙率、空隙等效直径、空隙数量等进行研究,并应用统计分析给出空隙等效直径的数学模型表征。

1 试验

根据马歇尔试验确定三种级配(SAC-16、AC-16、AC-13)沥青混合料的最佳沥青用量分别为3.91%、4.29%、4.37%,采用击实法和静压法(见JTG E20-2011)两种成型方法制作的不同级配类型的试件见表1,为提高数据的可靠性,每种类型试件制作3个,以下提及的空隙特征值均为3个同种类型试件的平均值。其中,沥青采用辽河AH-90#,其技术指标如下:针入度为86×0.1 mm(25 ℃);延度>100(15 ℃);软化度为45.5 ℃;密度为1.008 g·cm-3(25 ℃)。

表1 试件类型 Table 1 Specimen types

混合料的级配见表2。三种级配沥青混合料试件的目标空隙率均为4%。采用Siemens Somatom Sensation 16层螺旋X-ray CT扫描仪

表2 沥青混合料级配组成 Table 2 Gradation composition of asphalt mixtures %

进行沥青混合料内部空隙特征识别,X-ray CT扫描仪参数如下:扫描电流为120~340 mA;扫描电压为120 kV;准直器宽度为0.75 mm;探测器宽度为16 mm×16 mm;矩阵为512×512;图像分辨率为0.5 mm;床速为13.5 mm/r;扫描类型为断层扫描。沿试件水平方向,以厚度1 mm无间隔扫描。由扫描得到的图片发现,每组试件的上、下端部各5张图片黑白亮度异常,不具备研究条件,因此予以舍弃。这种现象主要是CT数异常引起的。CT数值表征了材料的密度分布,CT数愈大材料密度愈大,图像亮度越高。CT扫描仪发出的射线从空气到沥青混合料试件内部的过程中,途径介质的密度变化较大,使得局部CT数值突变,进而导致边缘亮度异常。

2 图像处理

为获取沥青混合料内部的空隙特征,需对CT图像进行图像处理。灰度宽度值 W与灰度中值 L是CT图像重要的灰度转化参数。通过反复的检验得出: W值的范围为700 ±150, L值的范围为1900±50。利用CT数实时反馈功能对沥青混合料图像中的集料、沥青胶浆及空隙各组分进行深入识别。根据文献[ 10]与本次CT试验的数据,确定CT数大于1950的图像代表粗集料;CT数介于1200~1950的图像代表沥青胶浆;CT数小于1200的图像代表空隙。根据Image Tool图像识别功能,并应用相应的转化函数将CT图像的色度与饱和度降低,

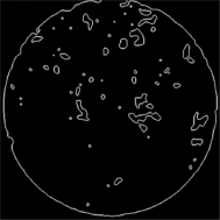
保留图像的亮度信息,最后将其转换为灰度图像(见图1)。目前,图像阈值选取方法较多,如灰度平均值法、基于最大方差理论的大律法、导数法等。通过比较分析,本研究采用双峰法与CT数相结合的方法,即用双峰法选定阈值的大概范围,再利用CT数反复调整,确定最优的图像阈值。利用该方法将空隙与粗集料提取出来,试件内剩余部分即为砂浆。由于6种沥青混合料扫描温度、光线强度和操作水平等因素不尽相同,因此不同成型方法和级配的试件内部材料阈值亦不相同,具体如表3所示。最后应用MATLAB软件提供的函数将灰度图像转换成二值图像(见图2)。基于已处理完成的二值图像,利用边界识别函数与探测器算子选取图像中的集料与空隙边界轮廓,如图3所示。识别图像边缘轮廓不但可以获取沥青混合料试件内部的集料与空隙的特征信息,而且为基于CT扫描图像建立细观数值模型奠定基础。

图1 空隙灰度图Fig.1 Gray graph of air voids

图2 空隙二值图Fig.2 Binary graph of air voids

图3 空隙轮廓图Fig.3 Contours boundary graph of air voids

表3 不同试件的材料阀值 Table 3 Materials threshold value of different specimens
3 空隙特征分析
3.1 不同级配的沥青混合料空隙特征

本研究中提及的空隙率是指沿试件高度方向每个横截面内空隙所占的面积比例,空隙数量是指沿高度方向每个横截面内空隙个数,平均空隙率和平均空隙数量是指计算试件全部截面空隙率和空隙数量的平均值。等效直径是指运用等效圆法计算每个横截面全部空隙直径的平均值,如式(1)所示;平均等效直径是指计算试件全部截面空隙等效直径的平均值,如式(2)所示。

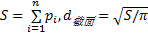(1)

(2)

式中: S为每一个截面空隙总面积; p为表征空隙面积的像素点面积; h为试件截面数量, d截面为每个截面的等效直径; d为试件的平均等效直径。

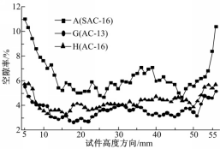
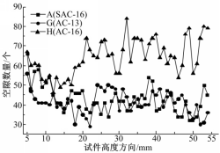
利用上述空隙特征指标不仅可以分析每个截面空隙的分布特征,而且可以研究空隙在整体试件中的分布规律。不同级配的马歇尔试件内部空隙率沿高度方向分布见图4。由该图可知,不同级配的马歇尔试件内部空隙率沿着高度方向总体呈对称分布, 即端部的空隙率较大,中部的空隙率较小。试件A的平均空隙率最大,且波动较大,尤其在两端部出现明显的突变现象,而试件G、H的空隙率波动较小,分别在3.31%和4.07%附近浮动。不同级配的马歇尔试件内部空隙数量沿高度方向分布见图5。由图5可见,试件H的平均空隙数量最大,沿高度方向的空隙数量波动亦最为显著。由此说明,马歇尔成型工艺下,断集配沥青混合料试件的粗集料可以相互嵌挤形成骨架,而细集料数量较少,并且混合料的内摩擦阻力较大,黏结力较小,因此虽然能够形成骨架,但残余空隙较大,从而SAC型试件的平均空隙率和平均空隙等效直径均较大。

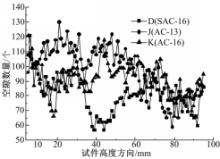
图4 马歇尔试件内部空隙率沿高度方向的分布Fig.4 Distribution of volume of air voids in Marshall specimens along depth

图5 马歇尔试件内部空隙数量沿高度方向的分布Fig.5 Distribution of number of air voids in Marshall specimens along depth

不同级配的静压试件内部空隙率和空隙数量沿高度方向的分布分别见图6和图7。从图6、图7可以看出,全部静压试件的空隙率和空隙数量沿高度方向波动均较大, 空隙数量变化均无明显规律;试件J与试件K的空隙率沿高度方向分布均呈逐渐增加的趋势。这是由于静压试件制作采用一个端部受力压实,作用力难以从试件一端均匀有效地传递到另一端,从而导致试件两端的空隙率分布呈现“一端大、一端小”的形状。在静压法成型工艺下,不同级配试件之间的平均空隙数量、平均空隙率及平均空隙等效直径的方差分别为5个、0.12%、0.28 mm,这说明静压试件中的空隙特征值相差较小和空隙分布较为接近。据此可以得出,静压成型法对不同种级配试件的内部空隙特征影响较小。

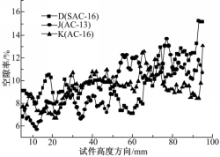图6 静压试件内部空隙率沿高度方向的分布Fig.6 Distribution of volume of air voids in static compacted specimen along depth

图7 静压试件内部空隙数量沿高度方向的分布Fig.7 Distribution of number of air voids in static compacted specimen along depth

3.2 不同成型方法的沥青混合料空隙特征

本研究针对两种不同成型方法的沥青混合料试件进行空隙特征分析。两种成型方法的沥青混合料内部空隙特征值如表4所示。由该表可知,马歇尔试件和静压试件的扫描计算空隙率均大于实测空隙率,且差异较小,其中相对误差最大值为0.98%,造成该误差的主要原因是由于图像处理中阈值选取精确度不足,而使空隙面积小于实测空隙面积,因此关于提高阈值选取精确度的研究是二维图像处理的重要方向之一。同时,由表4可得,SAC-16的马歇尔试件与静压试件的平均空隙率相差3.51%,平均等效直径相差0.05 mm;AC-13和AC-16的马歇尔试件与静压试件的平均空隙率分别相差6.07%、5.15%,平均等效直径分别相差0.6 mm、0.65 mm。由此说明,两种成型方法对SAC型试件的内部空隙特征影响较小,而对于AC型试件的影响较大。此外,由表4可知,在相同级配下,与马歇尔试件相比,静压试件的空隙空间分布离散性、平均空隙率和平均空隙数量均较大,其中三种级配试件(SAC-16、AC-13和AC-16)的平均空隙率分别增加了3.51%、6.07%、5.15%;平均空隙数量分别增加了43个、56个、28个;平均空隙等效直径增加较小,分别为0.05 mm、0.60 mm、0.65mm。另外,三种级配的马歇尔试件的平均空隙率与目标空隙率相差较小,分别为2.38%、-0.69%、0.07%,而静压试件的平均空隙率超出设计目标值1.4倍以上,这说明马歇尔试件的成型工艺较为符合设计要求。由于马歇尔试件为双面击实成型,且其试件高度比静压试件低,作用力可从试件的两端有效传递至内部,力的作用路径短,受力均匀,所以同级配下马歇尔试件的平均空隙率呈上下两端对称。此外,与同级配的静压试件相比,马歇尔试件内部空隙率沿高度方向的分布曲线的波动小,但采用两种成型方法的试件的空隙数量分布均无规律。

表4 试件空隙特征统计表 Table 4 Air voids characteristic

另外,与SGC成型试件内部空隙特征对比发现,马歇尔试件与SGC试件的空隙率分布规律相同,均为两端大,中间小,空隙数量变化均没有明显规律[ 11, 12]。由此表明,用马歇尔成型方法与SGC成型方法制作的沥青混合料的空隙率空间分布规律基本一致。SGC试件与静压试件的空隙分布规律相差较大。SGC成型方法具有较好的模拟性和数据采集的优越性,压实过程较接近路面的实际受荷载状态。马歇尔试件的内部空隙分布较为规律,平均空隙率与设计目标值相差较小,压实密度亦较为符合设计。因此马歇尔成型方法仍是我国今后一段时间所采用的主要混合料设计成型方法。

3.3 空隙等效直径的数学模型表征

目前利用数学模型表征沥青混合料内部结构各组分相的特征研究还处于初级阶段。Masad等[ 1]采用Weibull函数描述了试件内部空隙等效直径沿试件深度方向的分布状态。但由于Weibull函数中的尺寸参数与形状参数均为估算值,且该函数在描述空隙特征方面计算较为复杂,所以本研究尝试通过统计分析提出一个计算简单的两参数数学模型,进而对沥青混合料内部空隙等效直径在试件中的分布规律进行表征,具体数学模型为

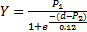(3)

式中: Y代表空隙等效直径累计百分率; P1、 P2为待定模型参数。

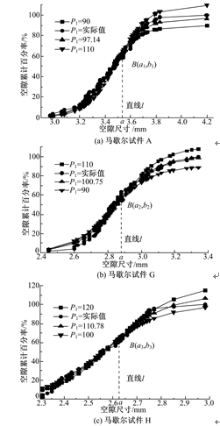
不同级配的马歇尔试件与静压试件的空隙等效直径数学模型拟合参数见表5。由表5可以看出,数据拟合参数的相关性较好,应用该模型可实现空隙特征的数学模型表征。为明确模型参数的物理意义,本研究针对两参数分别进行了参数敏感性分析,其中马歇尔试件的模型参数 P1的敏感性见图8。限于篇幅,本研究仅给出 P1的敏感性。

表5 拟合参数 Table 5 Fitting parameters

从图8可以看出,随着参数 P1值的变化,曲线总是围绕着某一个固定点 B转动,但三种级配对应的 B点坐标( a i, b i)( i=1,2,3)不同。以通过 B i点横坐标的铅垂线为轴,该直线右侧区域的面积变化较为明显,即当参数 P1值增大时,直线 l=a i右侧区域的面积随之增大,反之亦然。这说明参数 P1值的大小主要影响大于 a i值的空隙等效直径的数量。例如当某试件的空隙数量固定时,参数 P1值愈大,大于 a i值的空隙等效直径的数量愈大, 而小于ai值的空隙等效直径的数量愈少。通过分析大于ai值的空隙等效直径的层数所占试件全部层数的百分比,可以确定参数P1值的影响范围。通过计算得出,在不同级配条件下,马歇尔试件的模型参数P1的影响范围均为(38±1)%;静压试件的模型参数 P1的影响范围分别为36.7%、39.6%、41.25%。据此可以得出, P1反映了大于某一固定空隙尺寸的数量范围。此外,通过计算可得到参数 P2值与其相应的空隙等效直径的差值。

图8 马歇尔试件模型参数 P1的敏感性Fig.8 Sensitivity of model parameter P1for Marshall specimens

计算表明,不同级配的马歇尔试件的模型参数 P2与其相应的空隙等效直径的差值均为0.2±0.01;同理,静压试件的差值均为0.15±0.01。由此可以说明,利用差值可以判别试件的成型方法。但对不同成型方法的差值的精确值仍有待于深入研究。此外,本研究提出的数学模型的参数数量较少且计算简单,可以用来定量地分析不同成型方法和级配的沥青混合料空隙等效直径在其内部结构中的分布规律,据此为研究沥青混合料内部空隙特征的数学模型表征提供参考。

4 结论

(1)在不同级配条件下,SAC型马歇尔试件的空隙率沿高度方向分布的波动较大,AC型马歇尔试件的空隙率线形走势稳定,分别保持在3.31%、4.07%附近浮动,马歇尔试件的空隙数量波动无规律;SAC型与AC型的静压试件的平均空隙数量、平均空隙率及平均空隙等效直径均相差很小,表明静压成型法对不同种级配试件的空隙特征值影响较小。

(2)在同级配条件下,两种成型方法对SAC型马歇尔试件的内部空隙特征影响较小,而对于AC型试件的影响较大。静压试件的空隙空间分布离散性、平均空隙率和平均空隙数量比同级配的马歇尔试件的大;马歇尔试件内部空隙率沿高度方向的分布比静压试件的波动小,但采用两种成型方法的试件的空隙数量分布均无规律。

(3)通过统计分析提出的两参数数学模型可以较好地表征沥青混合料的内部空隙等效直径特征。其中,模型的两个参数 P1和 P2可分别表征沥青混合料内部空隙等效直径大小比例关系及其影响范围,以及成型方法。

The authors have declared that no competing interests exist.

参考文献
[1] Masad E, Jand hyala V K, Dasgupta N, et al. Characterization of air void distribution in asphalt mixes using X-ray computed tomography[J]. Journal of Materials in Civil Engineering, 2002, 14(2): 122-129. [本文引用:2] [JCR: 0.959]
[2] Masad E, Muhunthan B. Internal structure characterization of asphalt concrete using image analysis[J]. Journal of Computing in Civil Engineering, 1999, 13(2): 88-95. [本文引用:1] [JCR: 1.268]
[3] Wang L B, Frost J, Mohammad L, et al. Three-dimensional aggregate evaluation using X-ray tomography imaging[C]∥The 81st Annual Meeting of Transportation Research Board, Washington D C, 2002: 1-22. [本文引用:1]
[4] You Z P. Development of a micromechanical modeling approach to predict asphalt mixture stiffness using the discrete element method[D]. Urbana- Champaign: University of Illinois, 2003. [本文引用:1]
[5] Arambula E, Masad E, Martin A E. Influence of air void distribution on the moisture susceptibility of asphalt mixes[J]. Journal of Materials in Civil Engineering, 2007, 19(8): 655-664. [本文引用:1] [JCR: 0.959]
[6] 裴建中, 张嘉林. 矿料级配对多孔沥青混合料空隙分布特征的影响[J]. 中国公路学报, 2010, 23(1): 1-6.
Pei Jian-zhong, Zhang Jia-lin. Influence of mineral aggregate gradation on air void distribution characteristic of porous asphalt mixture[J]. China Journal of Highway and Transport, 2010, 23(1): 1-6. [本文引用:1] [CJCR: 2.996]
[7] 李芬, 沈成武. 基于CT图像的沥青混合料分形特征的研究[J]. 华中科技大学学报: 城市科学版, 2006, 23(2): 35-37.
Li Fen, Shen Cheng-wu. Study on fractal characteristics of asphalt mixture based on CT image[J]. Journal of Huazhong University of Science and Technology(Urban Science Edition), 2006, 23(2): 35-37. [本文引用:1]
[8] 汪海年, 郝培文. 沥青混合料微细观结构的研究进展[J]. 长安大学学报: 自然科学版, 2008, 28(3): 11-15.
Wang Hai-nian, Hao Pei-wen. Advances in microstructure study on asphalt mixture[J]. Journal of Chang'an University(Natural Science Edition), 2008, 28(3): 11-15. [本文引用:1]
[9] 李晓军. 沥青混合料破损识别与仿真[D]. 广州: 华南理工大学, 2004.
Li Xiao-jun. Damage identification and simulation of asphalt mixture[D]. Guangzhou: South China University of Technology, 2004. [本文引用:1]
[10] 李晓军, 张肖宁. CT技术在沥青胶结颗粒材料内部结构分析中的应用[J]. 公路交通科技, 2005, 22(2): 14-16.
Li Xiao-jun, Zhang Xiao-ning. Application of X-ray computerized tomography in analysis of inner structure of asphalt mix[J]. Journal of Highway and Transportation Research and Development, 2005, 22(2): 14-16. [本文引用:1] [CJCR: 0.844]
[11] Masad E, Tashman L, Somedavan N, et al. Micromechanics based analysis of stiffness anisotropy in asphalt mixtures[J]. Journal of Materials in Civil Engineering, 2002, 14(5): 374-383. [本文引用:1] [JCR: 0.959]
[12] Masad E, Button J W. Unified imaging approach for measuring aggregate angularity and texture[J]. Computer Aided Civil and Infrastructure Engineering, 2000, 15(4): 273-280. [本文引用:1] [JCR: 4.46]