张天霄(1986),男,博士研究生.研究方向:液压传动,可靠性设计.E-mail:zhangtx11@mails.jlu.edu.cn
The vibration theory is used to investigate the vibration situation of a hydraulic relief valve under hydrodynamic shock. The vibration model of the relief valve is proposed, the natural frequency and transient response of the relief valve are studied. Numerical simulation of the vibration of the relief valve is carried. Simulation results may provide the foundation for the working safety and reliability of the hydraulic relief valve.
振动与噪声是溢流阀存在的突出问题,尤其在高压大流量时,溢流阀的振动与噪声会更突出,甚至会出现系统的共振,使系统的振动超标,导致阀的损坏。目前有关液压阀研究主要集中在设计、试验、控制等方面,相关液压阀的振动分析文献却不多见[ 1, 2, 3, 4, 5, 6],但是液压阀的振动分析对提升液压阀的性能、减少液压阀的振动噪声、提高液压阀的工作效率等具有重要的意义。
本文提出了液压溢流阀的振动分析方法,应用振动理论[ 7, 8, 9, 10],充分考虑液压冲击的作用,导出了液压溢流阀的固有频率和瞬态响应的解析形式,从而分析了液压阀的振动状况,很好地解决了液压溢流阀的振动问题,通过计算机程序实现对液压溢流阀的动态数值分析,为液压阀的安全可靠工作提供了理论根据和技术保障。
在突然关闭和开启液压阀的液体管道中,液压振动冲击使管道和阀产生振动冲击,这种瞬变的冲击和压力将导致液压管道和阀的破坏。以图1所示的液压溢流阀为例,当液压溢流阀突然关闭液流时,液体立即停止流动,则液压振动冲击的压力升高值[ 11, 12, 13, 14]为
 | (1) |
式中:Δ p为液压振动冲击的压力升高值(Pa); ρ为液体密度(kg/m3); v为管道中液体流动的速度(m/s); v c为冲击波在管道中的传播速度(m/s);其中 v c为
 | (2) |
式中: K为液体体积弹性模量(Pa); d为管道内径(m); E为管道材料的弹性模量(Pa); δ为管道的壁厚(m)。
式(1)适用于液压阀关闭和开启为瞬时完成的情况,即液压阀关闭和开启管道中的液流时间小于压力波来回传递一次所需要的时间,即
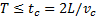 | (3) |
式中: T为液体阀关闭管道液流停止流动的时间(s); t c为临界关闭时间(s); L为从液压阀到系统中管道的长度(m)。
由于液压振动冲击是一种非常复杂的非定常流动的动态过程,虽然可以依据式(1)计算瞬时突然关闭和开启液压阀导致的液压振动冲击的压力升高值Δ p。但是在工程实际中,关闭和开启液压阀是需要一定时间的,可见很难精确地估计液压振动冲击的压力升高值Δ p,因此Δ p可以近似地表示为[ 12, 13]
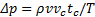 | (4) |
满足式(3),称为完全冲击,否则便是非完全冲击,非完全冲击引起的压力升高值比完全冲击时的低。
虽然影响液压溢流阀的振动与噪声的因素很多,如油液振动、空穴和液压冲击、阀的撞击和磨擦等。但是在振动模型的简化中,主要考虑了锥阀质量和弹簧元件的存在与油液的阻尼因素以及外加液压振动冲击等的激励作用,构成了简化的质量-阻尼-弹簧系统的振动模型(见图1),据此可以应用振动理论建立溢流阀的振动模型,研究推导溢流阀的固有频率和分析影响因素。设阀芯的当量质量为 m(kg)、弹簧刚度为 k(N/m),则溢流阀系统的固有频率为
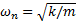 | (5) |
可见溢流阀的结构参数(锥阀质量和弹簧刚度)决定了溢流阀系统的固有频率,因此阀系统是否发生共振取决于在设计溢流阀相应的结构参数时要充分考虑溢流阀的工作环境,避免激振力频率 ω与系统固有频率 ω n相接近。
液压溢流阀在工作过程中,必然受到油液阻力影响。若已知阻尼系数 c(N·s/m),经过推导可以确定临界阻尼系数 cc(N·s/m)为
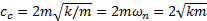 | (6) |
引进阻尼比 ζ (或称相对阻尼系数),有
 | (7) |
式中: ζ为一无量纲的量。可见阻尼比 ζ决定于溢流阀系统的锥阀质量和弹簧刚度以及油液的阻尼系数,因此设计溢流阀相应的结构参数时要充分考虑抑制系统振动的问题。
考虑小阻尼情况(即ζ<1, c< c c),则有阻尼自由振动的固有频率为
 | (8) |
当液压溢流阀在工作时,为了避免共振现象的发生和有效地抑制振动与噪声,必须清晰溢流阀的固有频率和相应的影响因素。
在计算液压振动冲击引起管道和阀的振动时,设液压阀的关闭和开启为瞬时完成,因此可以认为液压阀的关闭和开启将产生脉冲激励,并引起脉冲响应。以液压溢流阀系统为对象,并根据脉冲力 F( t)= ΔpAδ( t)确定系统的响应,系统振动微分方程为
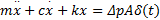 | (9) |
式中: A为液压阀与油液接触的当量面积(m2); δ( t)为系统的单位脉冲,其函数为无量纲函数。
若系统在脉冲力作用之前静止,脉冲力使速度产生瞬时变化,可以认为在 t=0时作用的脉冲力等效于初始位移 x(0)=0和初始速度 v0= ΔpA/ m的初始干扰作用,所以方程(9)等价于初始条件引起的自由振动,即
 | (10) |
其解为
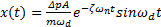 | (11) |
据此可以确定溢流阀系统在液压振动冲击输入作用下的响应输出量的变化过程。
在一液压管路系统中,某一液压溢流阀的当量阀芯质量 m=7.5×10-2 kg、弹簧刚度 k=1.3×104 N/m,阻尼系数 c=5 N·s/m,阀断面直径 dv=6 mm,管道内径 d=6 mm,管壁厚度 δ=1 mm,工作时油液的流速 v=1 m/s。若已知液压油的体积模量 K=1.226×103 MPa,管道的弹性模量 E=2.06×105 MPa,液压油的密度 ρ=900 kg/m3,若液体阀关闭,管道液流停止流动的时间 T=0.5 s,从液压阀到系统中管道的长度 L=1 m。如果液压换向阀突然关闭或开启,在管道产生液压振动冲击时,试分析液压溢流阀的振动状况。
根据已知的条件和给出的数据,计算可得冲击波在管道中的传播速度 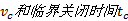
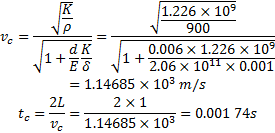
在液压阀开启和关闭时,管道和阀会受到液压振动冲击的影响。管内的压力升高Δ p为
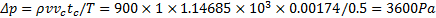
溢流阀与油液接触的当量面积 A为
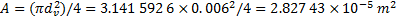
相对阻尼系数 ζ为
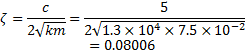
系统固有频率为
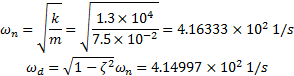
可见当相对阻尼系数 ζ较小(即 ζ≪1)时,有阻尼的固有频率 ω d 与无阻尼的固有频率 ω n 相差甚小,因此相对阻尼系数 ζ较小的情形可以忽略阻尼对系统频率的影响。
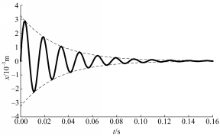
对此溢流阀系统进行求解,计算出等效质量 m的位移 x( m)随时间 t( s)的变化曲线(见图2)。
由图2可见,溢流阀系统的振幅被限制在曲线 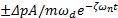
应用振动分析方法,充分考虑引起液压溢流阀振动和噪声的因素,可以正确地反映液压溢流阀的动态特性,建立了可供实际计算的在液压冲击状况下的溢流阀振动模型,估计或预测溢流阀在规定的工作条件下的振动状况,揭示了液压溢流阀产生振动和噪声的机理。应用本文方法对液压溢流阀进行振动分析,可以提高液压溢流阀的设计水平。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|