Bootstrap是对已知数据的再抽样^{[ 10, 11]}。设 T=( T₁, T₂,…, T _n)是总体 F( T)的独立同分布的样本数据, F _n ( T)是由样本数据 T得到的分布函数,参数估计为 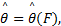则样本分布参数与总体参数的误差为

(1)

从样本总体 F _n ( T)中再次抽取子样本数据, 是由子样本数据 T^* 得到的分布函数,其参数估计为 则子样本分布参数与样本分布参数的误差为

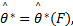
(2)

如果 Δ^*在可接受范围内,则可以用子样本的分布 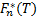近似代替样本的分布 F _n ( T)。

Bootstrap方法的误差来源于样本抽样和子样本再抽样过程。若要减小估计参数的误差,则必须减小抽样误差和再抽样误差。减小误差的方法有扩大样本容量和多次抽样两种方法。

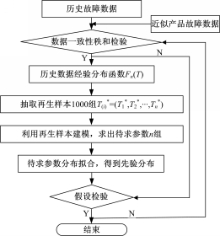
根据抽样方式的不同,Bootstrap方法分为参数与非参数抽样。参数抽样方法常用于抽样函数分布已知的情况,从中抽取再生样本的一种抽样方法,因此参数抽样方法比非参数抽样方法效率和精度更高^{[ 12]}。基于数控机床产品的特点,其故障数据一般服从威布尔分布^{[ 7]},因此对数控机床产品的数据进行抽样时一般用Bootstrap参数抽样方法,并在此基础上确定Bayes的先验分布,其流程如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 Bootstrap抽样方法流程图Fig.1 Flow chart of Bootstrap sampling

Bootstrap再抽样与一次抽样相比,减少了分布函数的抽样误差,因此本文在经验分布函数的基础上运用参数抽样方法进行再抽样,通过Gibbs抽样计算得到威布尔分布参数 α和 β的先验分布。

先验分布 π( θ)是以经验或者同类产品的故障数据为基础对总体分布参数做出的估计。在获取样本数据之后,对 π( θ)进行修正,可得到后验分布 π( θ| x),即总体分布^{[ 13]},为

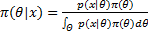(3)

式中: p( x| θ)为参数 θ的似然函数; π( θ)为参数 θ的先验分布。

相对于经典统计方法,Bayes方法的后验分布计算复杂,而蒙特卡罗抽样是处理复杂统计问题的重要方法,因此可利用其从 π( θ| x)中抽取样本 θ={ θ₁, θ₂,…, θ _n},则:

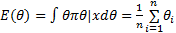(4)

Gibbs抽样是蒙特卡罗抽样方法的一个特例,可用于后验分布的计算^{[ 14]}。在对高维或复杂分布进行抽样时,通过 的条件分布族构造一个不可约正常返的马尔可夫链(Markov Chain,MC):

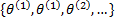(5)

当式(4)中 n的取值足够大时,式(5)则是以 π为不变分布,即该分布的值接近于 π。因此式(5)可以近似地作为分布 π的总体样本^{[ 15, 16]}。

在马尔可夫链蒙特卡罗抽样方法中,给定条件分布 π( X _T | X_-T),其中 X _T={ X _i,i∈T}, X-_T={ X _i,i∉ T},并且 T⊆ N={1,2,…, n},则如果π( X _T | X_{- T})条件分布中所有变量都出现的分布为满条件分布。后验分布 π( θ)通常是乘积式,因此满条件分布与抽样分布相差一个比例常数。如果不考虑此常数,则可以用满条件分布的样本近似代替抽样分布的样本。给定参数初值 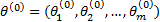,设t=(t₁, t₂,…, t _n)为一组观测样本, M次迭代后结束。

Gibbs抽样步骤如下^{[ 17, 18]}:

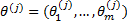
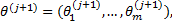
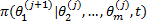
步骤1 根据下面的满条件分布,从 抽取 则

︙

︙

步骤2 重复迭代 M次,此时样本趋于收敛,即 可用,令

步骤3 重复步骤1,直到序列式(6)达到收敛。

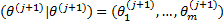(6)

序列式(6)达到收敛后得到参数的抽样值如下:

︙

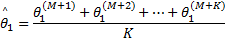
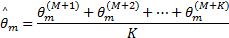
在获得 θ_i的抽样值后,则用MCMC方法计算Bayes的后验分布。

将表1的故障数据按大小排序,根据Bootstrap再抽样方法,利用Matlab对其进行循环计算,每次计算时去掉一个数据,对剩余的数据进行两参数威布尔分布函数的拟合,分别求得参数 α _i 和 β _i,则

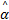
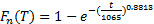将 和 代入经验分布函数 F _n ( T),则

(7)

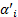
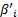
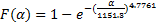利用Matlab对函数 F _n ( T)随机抽取1000组再生子样本,然后对该子样本分别进行分布拟合,求得1000组的 和 ,从而得到 α和 β的先验分布:

(8)

(9)

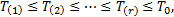
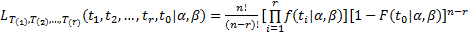假设该批加工中心主轴系统可靠性现场试验的截止时间为 t₀共有 n个样本和 r个故障,其顺序统计量为: T₍₁₎≤ T₍₂₎≤⋯≤ T_(r)≤ T₀, 相应的观测值为则其联合概率密度函数为

(10)

以 Z₅ 加工中心主轴为例进行后验分布的计算说明。将其故障数据代入式(10)(其中样本数 n=6,故障数 r=5,故障间隔时间服从两参数威布尔分布函数),则最大似然函数:

(11)

其中,式(11)的核为

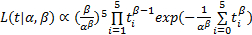(12)

根据Bayes公式,得到 α和 β的后验分布:

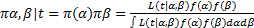(13)

将 Lt| α, β, fα和 fβ代入式(13),得到后验分布的核为

(14)

根据满条件定义, α和 β的满条件分布为

(15)

(16)

根据后验分布式(3),建立Dooble模型,如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 Gibbs抽样的Dooble模型Fig.2 Dooble model of Gibbs sampling

α、 β和 γ分别表示威布尔分布中的尺度参数、形状参数和尺度参数。在进行Gibbs抽样时,取初始值 α=1111, β=0.8528和 γ=0,迭代次数取10 000次,运用Gibbs的编程语言Winbugs对Dooble模型进行求解,结果如表3和表4所示。

表3

Table 3

表3(Table 3)

表3 后验分布中尺度参数 α的数字特征 Table 3 Characteristics of posterior distribution of α 均值 MC误差 2.50% 组中值 97.50% 开始点 样本数 1112.0 0.446 690.3 1115.0 1519.0 501 247500 1112.0 0.405 689.7 1114.0 1519.0 501 297500 1111.0 0.3755 690.3 1114.0 1519.0 501 347500 1111.0 0.3497 690.5 1114.0 1518.0 501 397500 1111.0 0.3306 690.5 1114.0 1518.0 501 447500

表3 后验分布中尺度参数 α的数字特征 Table 3 Characteristics of posterior distribution of α

表4

Table 4

表4(Table 4)

表4 后验分布中形状参数 β的数字特征 Table 4 Characteristics of posterior distribution of β 均值 MC误差 2.50% 组中值 97.50% 开始点 样本数 0.8528 2.605E-4 0.5925 0.8596 1.076 501 247500 0.8528 2.336E-4 0.5922 0.8596 1.076 501 297500 0.8528 2.155E-4 0.5919 0.8596 1.076 501 347500 0.8528 2.004E-4 0.592 0.8595 1.076 501 397500 0.8529 1.916E-4 0.5919 0.8597 1.076 501 447500

表4 后验分布中形状参数 β的数字特征 Table 4 Characteristics of posterior distribution of β

由表3和表4可知,随着迭代次数的增加,MC抽样误差逐渐减小,均值和标准差逐渐趋于稳定,即迭代过程中马尔可夫链达到稳定,迭代函数收敛。

可知 α=1111和 β=0.8528,因此 Z₅加工中心主轴系统的失效率函数和可靠度函数分别为

(17)

(18)

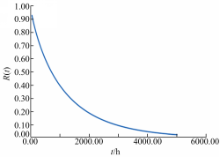
可靠度和概率密度函数曲线如图3和图4所示。根据平均故障间隔工作时间(Mean time between failures,MTBF)的定义, Z₅的MTBF=1206.2 h。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 加工中心主轴系统可靠度函数曲线Fig.3 Reliability function of machining center spindle

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 加工中心主轴系统失效率函数曲线Fig.4 Failure rate function of machining center spindle