陈吉清(1966),女,教授,博士生导师.研究方向:车身结构与安全.E-mail:chjq@scut.edu.cn
为预测和评判汽车碰撞事故中乘员胸部肋骨骨折引起的胸部损伤,对一位中国成年男性志愿者进行CT扫描,建立了具有人体解剖学结构的肋骨有限元模型。为提高模型的生物仿真度,通过动物组织反求试验获得肋骨材料参数。模型用Kindig所做的人体肋骨载荷试验进行验证,并与直接引用参考文献材料参数得到的仿真数据进行比较。结果表明:其位移-反作用力曲线与试验曲线吻合较好;采用反求方法获取的材料参数进行仿真计算时肋骨具有更好的生物仿真度。
In order to predict and evaluate the human thoracic injuries caused by rib fracture in car crashes, a finite element model of human ribs having the features of human anatomy structure is established and verified based on the CT scanning of a 50 percentile Chinese male volunteer. To improve the model's biological fidelity, the material parameters of ribs are gained by reverse experiment of animal tissue. The model is verified by the Kindig's load experiment of human body ribs and compared with the simulation data, which the material parameters were cited directly from the reference. The results show that the reaction force-displacement curve agrees well with the experimental curve and the model has a better biological fidelity when the material parameters were gained from the reverse engineering method.
Harm利用美国国家事故采样系统(NASS)中的数据统计整理的道路交通事故中人体各部位损伤比例分别是:头部35.3%,面部2.8%,颈部4.6%,胸部26.7%,腹部18.2%,上肢4.1%,下肢5.1%[ 1]。可见,在汽车碰撞事故中胸部损伤仅次于头部损伤,其中肋骨骨折是最常见的胸部损伤类型。因此,研究胸部肋骨的损伤机理对于改善与优化汽车的设计,采取安全的防护措施和降低伤害的发生率具有重要的意义。随着计算机技术的不断发展,有限元模型成为研究胸部肋骨损伤生物力学的重要工具[ 2]。近年来研究人员开始用有限元方法开发了各种胸部有限元模型并进行了验证,但是很少有文献对肋骨进行单独的仿真验证,而且模型的材料参数基本上是直接引用国外经典文献的材料参数。由于生物材料的复杂性及试验样本的差异,同一种生物组织的材料参数在不同的文献中通常具有较大的差异,甚至相差一个数量级。因此,直接采用国外经典文献的材料参数,对模型的生物逼真度有一定的影响。
本文利用CT扫描数据,建立了具有解剖学结构的人体胸部肋骨有限元模型。为提高所建模型材料参数的准确度,肋骨的材料参数通过以下两种途径获取:一是直接引用相关经典文献中的材料参数;二是进行动物组织试验,并结合有限元分析技术和优化算法对肋骨的材料参数进行反求。将两种途径获取的材料参数分别用于所建立的肋骨模型,并采用维吉尼亚大学Kindig等[ 3]于2009年所做的人体肋骨载荷试验数据对两组仿真进行验证,结果表明,其位移-反作用力曲线与试验曲线吻合较好,并且采用反求方法获取的材料参数进行仿真计算时具有更好的生物仿真度,该模型可以用于胸部肋骨损伤机理和安全防护研究,并为后续整个人体有限元模型的开发奠定了基础。
肋骨是典型的硬组织,具有弹塑性性能,因此采用三点弯曲试验进行材料参数反求。三点弯曲试验测试方法简单,样件易于制作,结果重复性好。由于受道德、宗教、实施复杂性、可重复性及试验成本等方面的限制,不能直接对人体肋骨进行试验,本文采用与人类骨骼理化性能和力学性能相近的猪肋骨[ 4]进行冲击模拟试验。
三点弯曲试验是指将肋骨两端支撑,在中部施加载荷。根据载荷速度的不同,三点弯曲试验可分为准静态试验和动态试验,本试验采用的是准静态试验。
从市场购置了冷冻4日的成年白猪肋骨若干,剔除软组织,刮除骨髓和骨膜,用锯骨机将肋骨切成等长的骨条试件,获得3根样本。在试验前用Atos光学扫描仪扫描得到各样本的图像数据,用于重建其三维几何模型。试验采用的是Sans大门式微机控制电子万能试验机。试验时控制为低速准静态加载,各样本加载速度均为50 mm/min,加载点为其中心点位置,图1为三点弯曲试验装置图:
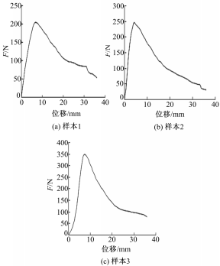
图1中钢制冲击块通过一销头固定到Sans的载荷锤头,冲击块圆柱及支架顶端两支撑圆柱直径均为12 mm,支架间距(即试件跨距)为100 mm。试验前控制冲击块刚好接触猪骨表面位置,加载开始后直至猪骨骨折试验即自动结束。利用微机数据采集系统获得到试验过程中各样本的位移-加载力曲线,如图2所示:
(1)肋骨有限元模型的建立
本文通过Atos光学扫描仪获得各试验样本的图像数据,其真实完整地描述了样本的三维体轮廓信息,由此建立了其三维几何模型,见图3:
利用专用的有限元网格划分软件对试验样本的三维几何模型进行网格划分,模型全部使用六面体实体单元建模。相比于四面体网格模型或四面体/六面体混合模型,全六面体网格模型计算精度更高,可获得更准确的模型响应。为了确保模型的精度和计算效率,在模型网格划分时对网格质量进行控制。对肋骨所有单元进行质量检查:最小长度为2.5 mm;最大长度为4 mm;长宽比率为1~4;翘曲为0~8;四边形角度为68°~111°;雅克比系数为0.65°~1°。通过模型简化、网格调整使所有单元都符合要求。
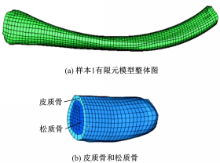
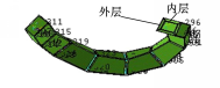
3个试验样本的有限元模型节点和单元数分别如下:样本1节点10 300个,单元8452个;样本2节点4402个,单元3500个;样本3节点7738个,单元6624个。图4(a)为样本1的有限元模型。骨骼结构分为皮质骨和松质骨,在划分有限元网格时,将模型分为内外两层,分别代表皮质骨和松质骨,如图4(b)所示:
三点弯曲试验结束后测量各个试验样本断截面的皮质骨实际厚度,其平均值为3.5 mm,以此为参考值设置皮质骨网格划分厚度。
(2)肋骨三点弯曲有限元仿真模型设置
在有限元仿真模拟中对动物骨骼组织多采用弹性材料、各向同性弹塑性材料、弹性横向各向同性材料等。其中皮质骨常采用弹性材料、各向同性弹塑性材料等,对松质骨常采用各向同性弹塑性材料和黏弹塑性材料[ 5, 6]。本文中皮质骨和松质骨均采用弹塑性材料。
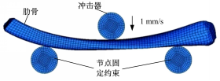
根据猪肋骨标本试验,肋骨准静态三点弯曲仿真设置如图5所示:
在仿真模型中,肋骨水平放置在两个刚性体支撑上,同时约束两个支撑,使其固定。冲击器用圆柱体模拟,并定义为刚体,只保留其在竖直方向的自由度。
仿真计算在LS-Dyna中进行,冲击器以恒定速度冲击肋骨中心位置,如图5所示。考虑到计算时间问题,冲击器的撞击速度适当增大至1 mm/s,这个速度比较低,仍属于准静态过程,并通过质量缩放对计算时间进一步控制。仿真中输出冲击器的接触力与其位移的关系曲线。
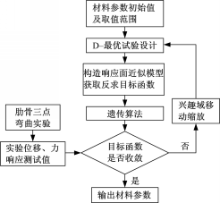
参数反求过程实质是将仿真计算和优化算法相结合,通过优化算法不断调整仿真模型的参数使仿真结果逼近试验结果。本文采用序列响应面方法,在各个设计子域中构建设计目标的近似模型,然后通过遗传算法寻优及兴趣域的移动和缩放来不断更新近似模型,直到优化过程收敛[ 7]。采用这种方法可以减少调用正问题的次数,从而提高材料反求的计算效率,整个流程如图6所示:
肋骨在碰撞中的生物力学响应主要取决于其皮质骨的力学性能。表1为皮质骨和松质骨的材料特性:
| 表1 皮质骨和松质骨的材料特性 Table 1 Material properties of the compact bone and spongy bone |
文献[8]研究了在分别改变肋骨的杨氏模量、屈服应力、切线模量和失效应变参数30%的情况下对肋骨断裂时的应力和位移的影响。结果显示,杨氏模量和屈服应力对仿真结果影响最大。本文主要对肋骨皮质骨的杨氏模量和屈服应力进行材料反求,其他参数参考文献[9]。反求参数范围参考文献[10],它总结了相关学者通过试验获取的肋骨材料参数,研究表明肋骨在三点弯曲试验下杨氏模量的取值范围为1.1~17.7 GPa,屈服应力的取值范围为30~100 MPa。
在优化过程中,主要对比仿真和试验中力-位移曲线,使仿真曲线与试验曲线尽可能吻合。当目标函数达到最优时,3个样本仿真模型的力-位移曲线与试验曲线的对比如图7所示:
表明肋骨材料参数优化后,与试验结果非常接近。优化后的肋骨皮质骨的弹性模量和屈服应力见表2:
| 表2 反求参数初始值、范围与收敛结果 Table 2 Reverse parameter initial value, the range and convergence results |
对一位男性志愿者进行CT断层扫描,扫描层厚为0.6 mm。首先从最初的CT数据进行医学影像的肋骨轮廓边界的分割提取;然后把分割提取出来的各断层医学图像进行影像配准;最后将正确配准叠加起来的各断层CT图像运用三维重构技术建立肋骨的几何模型。
本文利用专用的有限元网格划分软件对第六根和第十根肋骨的三维几何模型进行网格划分,模型全部使用六面体实体单元建模。建立肋骨有限元模型主要步骤如下:
(1)将处理好的肋骨曲面几何模型导入专用软件的网格划分模块中,旋转观察模型的几何特征,构思创建Block的方法,如图8所示:
(2)创建Block,并用Split Block工具对Block进行雕琢,得到Block拓扑结构,如图9所示:
(3)使用Associate工具将Block上的顶点关联到模型表面上,如图10所示:
(4)利用网格划分功能把Block分割成内外两层结构,如图11所示:
(5)点击模型树上的Pre-mesh选项,可以网格进行预划分操作,观察模型质量是否理想,并能借助Pre-mesh Quality工具查看模型质量分布值,如图12所示:
(6)对模型网格质量适当调整,检查合格后将预网格转化成非结构体网格完成网格划分,按照需要将划分的有限元模型以适当格式输出,输出后导入CAE软件,如图13所示:
为了确保模型的精度和计算效率,在模型网格划分时对网格质量进行控制。依据实体单元网格质量控制标准,如表1所示,对肋骨所有单元进行质量检查。通过模型简化、网格调整使所有单元都符合要求。
为提高人体模型的生物逼真度,进行单个组织的验证十分必要。因此,本文参考维吉尼亚大学Kindig等[ 3]于2009年所做的人体肋骨载荷试验对建立的肋骨模型进行验证。
试验验证第六、第十根肋骨,两根肋骨从男性尸体上与脊椎等分离开所得,与肋骨相连的所有肌肉、韧带等软组织全部被剔除。试验过程中肋骨的底端约束5个自由度,仅可绕 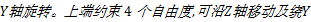

仿真模拟中分别采用通过反求获得的材料参数和直接从参考文献获得的材料参数。对每根肋骨的两端截取一部分定义为刚体,以模拟试验夹具对试验的影响。约束及加载条件如试验方法所述,在上端所有节点以恒定速度加载。
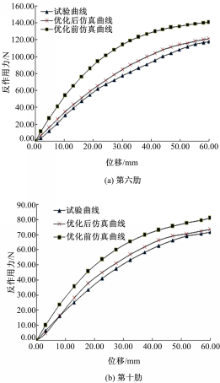
仿真输出了各肋骨底端反作用力与位移的对应关系,并与原试验作了比较,如图14所示:
图中参数优化前仿真曲线的材料参数直接引用参考文献;参数优化后仿真曲线的材料参数通过反求方法得到。
从图14可以看到,当直接引用参考文献的材料参数进行肋骨有限元模型的仿真验证时,虽然在趋势上跟试验一致,但是两者的反作用力值相差比较大。当采用反求方法获取的材料参数进行仿真验证时,仿真曲线不仅在整个历程的变化趋势上与试验曲线一致,而且其反作用力大小均与原试验大致相同。结果表明,通过动物组织的材料参数反求方法获取材料参数是可行的,而且可以有效提高模型的生物仿真度。
本文建立的肋骨有限元模型在仿真验证中的响应与人体肋骨载荷试验曲线的相应区间的响应能较好地吻合,表明所建立的模型具有较高的生物仿真度,可以用于胸部肋骨损伤机理和安全防护研究,并为后续整个人体有限元模型的开发奠定了基础。CT影像数据可以很好地体现骨骼等硬组织的细节,因此,对于建立骨骼组织的生物力学有限元模型,可以通过CT影像数据获得三维结构,然后利用网格划分软件生成六面体有限元网格。通过动物组织试验,进行材料参数反求,并将反求获取的参数用于仿真模型。通过对比发现,由反求方法获取的材料参数可以明显提高模型的生物仿真度。对于人体其他组织的材料参数也可以通过类似的方法进行反求来获得。本文重点剖析了人体第六、第十根肋骨的参数反求和建模,胸腹部的其他结构也可以类似地完成模型化工作,而且骨骼组织的其他参数,如泊松比、剪切模量、切线模量的反求问题也可做类似的研究。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|