李世武(1971),男,教授,博士生导师.研究方向:交通环境与安全技术.E-mail:shiwu@jlu.edu.cn
采用双自由度非独立悬架车辆1/2振动模型,以路面不平度为激励,运用随机振动理论建立了车辆振动微分方程,并使用Simulink对不同工况下车辆的悬架特性进行了仿真分析。基于对悬架特性的分析,设计了一种带过载保护装置的悬架载荷测量装置,提出了一种车辆载荷状态监测方法,以解放赛龙为试验车辆开发了车辆载荷状态监测平台,编写了传感器信号处理和载荷状态辨识程序,并对该系统进行了载荷状态检测试验和质心位置监测试验,结果表明测量误差小于5%,实现了车辆水平质心测定,为车辆在途危险状态的实时监测预警提供了技术支持。
A two-degree of freedom 1/2 vehicle vibration model of axle suspension was built. Using random vibration theory, the differential equation of vehicle vibration was derived with the road roughness model as the input excitation. The vehicle suspension characteristics under different working condition were simulated and analyzed using Simulink software. Based on the analysis of the suspension characteristics, a suspension load monitoring device with overload protection function was designed, and a method to monitor the vehicle load status was proposed. Furthermore, a vehicle load status monitoring platform for FSAW truck was developed. The program of sensor signal processing and vehicle load identification was written. The system was tested by load status detecting trial and centre-of-mass position monitoring trial. The results show that the relative measurement error is less than 5%, and the horizontal centre-of-mass of the vehicle was positioned accurately. This research provides technical support for the real-time monitoring and warning of vehicle in-transit risk status.
装载状态异常是导致营运车辆事故主要原因之一,我国每年由于此类原因引发的交通事故占营运车辆交通事故的60%以上,对车辆载荷状态的有效监控是避免此类事故的最佳方法[ 1, 2]。为了实现对车辆装载状态的实时监测,本文通过建立二自由度车辆1/2悬架振动模型,以路面不平度为激励输入,分析不同工况下悬架动态特性,并根据此特性开发了一种基于位移传感器的悬架载荷检测装置,提出了悬架载荷和水平质心位置的动态检测方法,以解放赛龙重型载货汽车为试验车辆,C9S12XEP100单片机为车载终端,在LabVIEW语言环境下编写程序实现了信息处理和显示[ 3, 4],开发了一种新的车辆载荷状态监测方法。
车辆悬架振动特性的分析过程参考汽车理论内容[ 5],通过建立非独立悬架车辆1/2振动模型,以路面不平随机高程作为模型输入,分析得到悬架振动位移与载荷状态的关系。
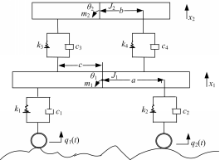
根据非独立悬架后桥结构建立基于路面不平度的1/2车辆振动模型,如图1所示:
由于载货汽车载荷大部分作用于后轮上,所以只考虑垂直振动和侧倾振动。图中,m1为非悬挂体系质量;m2为悬挂质量; a为车辆左右轮到车桥质心距离; b为悬架到悬挂质量质心距离;c为悬架到车桥质心距离;c1,c2为轮胎阻尼;c3,c4为悬架阻尼;k1,k2为轮胎刚度;k3,k3为悬架刚度;J1为车桥转动惯量;J2为车身转动惯量;θ1为车桥侧倾角;θ2为车身侧倾角。
根据牛顿第二定律建立振动微分方程:

式中:z1、z2为轮胎垂直变形量;z3、z4为悬架弹性元件垂直变形量,可用悬架体系垂直方向位移x1和车身垂直方向位移x2表示:
(1)
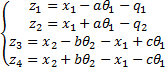 | (2) |
(3) 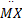
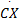
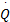
M = 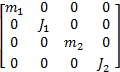
C q = 
K q = 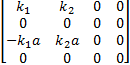
Q = 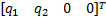
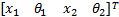
C = 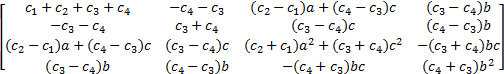
K = 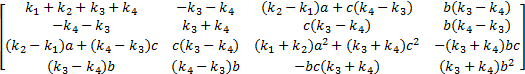
M为质量矩阵; C为阻尼矩阵; K为刚度矩阵; C q、 K q为路面不平度系数矩阵; q1、 q2为左右车轮路面不平整度值。
根据中国标准《 GB-7031》[ 6],路面不平度功率谱密度拟合公式为
G q 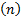
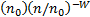
考虑到车辆行驶速度的影响,将路面不平度空间频率功率谱密度转换成时间功率谱密度:
G q 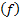

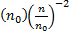
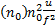
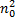
当 ω→ ¥时, G q( ω)→0,因此考虑下截止角频率 ω0之后,功率谱密度表示为
G q
 | (6) |
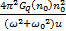
式(6)可看作白噪声激励的一阶线性系统响应。由振动理论知:G0 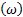
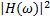
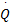
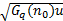
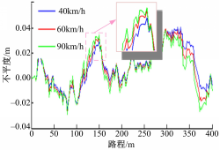
不同行车速度下路面不平度仿真波形如图2所示:
从图中可以看出,随着车速的增加,路面不平度曲线波动范围有所增加,车辆行驶在路面上的振动幅度也随之增大。
考虑到微分方程状态空间模块化方法在处理复杂系统多输入输出方面的优势[ 9],本文采用此方法进行振动特性仿真。
首先,将微分方程(3)变换为状态方程:
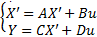 | (8) |
式中: X '= 
A = 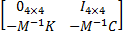
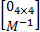
输出系数阵 C、 D根据所需的输出结果而定,解放赛龙载货汽车仿真参数如下:簧上质量 m整为4880 kg,簧下质量 m1为716 kg,悬架阻尼系数 c3、 c4为3031 N·s·m-1,轮胎阻尼系数 c1、 c2为10530 N·s·m-1,钢板弹簧刚度 k3、 k4为10760 N·m-1,轮胎刚度 k1、 k2为1106761 N·s·m-1,车辆左右轮到车桥质心距离 a为0.9 m,悬架到簧载质量质心、车桥质心距离 b=c=0.6 m,车身转动惯量 J2=2132 kg·m2,车桥转动惯量 J1=334 kg·m2。
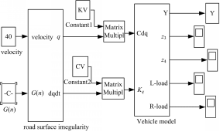
使用MATLAB软件的Simulink工具包进行仿真,其模块主要构架如图3所示,模型输入为车速、路面等级和装载质量。输出为悬架变形量和悬架动载。
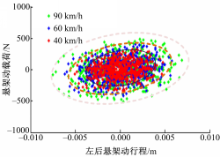
研究车速对悬架动态特性的影响:使车辆处于空载状态 m空=4880 kg,行驶在A级路面上, G q( n0)=1.6×10-5,车速为40、60、90 km/h时车辆后悬架动行程与动载荷相平面分析如图4所示:
当载荷一定时,悬架动行程和动载荷相点成准周期振荡稳定状态,并且随着车速的增加,悬架动行程和悬架动载荷的振动幅度都有明显的增大。车速为40、60、90 km/h时左侧悬架动载荷分别占悬架静载的1.45%、0.83%、0.67%,车辆行驶过程中悬架行程和悬架动载荷呈全局线性关系。
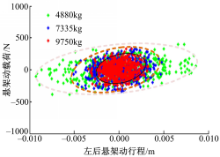
研究车载状况对悬架动态特性的影响:车身质量为4880、7335、9750 kg时,车辆以40 km/h速度行驶在A级路面, G q( n0)=1.6×10-5情况下分析悬架的动态特性,车辆后悬架动行程与动载荷相平面分析如图5所示:
由图5可以看出,当速度一定时,悬架动行程和动载荷相点呈准周期振荡稳定状态,并且随着车辆装载质量的增加,悬架动行程和悬架动载荷的振动幅度都有明显增大。车身质量为4880、7335、9750 kg时左侧悬架动载荷分别占悬架静载的0.71%、0.87%和1.07%。车辆行驶过程中悬架行程和悬架动载荷呈全局线性关系。
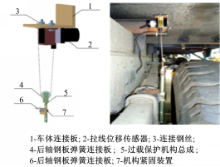
根据分析得到的悬架行程和悬架动载荷呈全局线性关系,本文研究开发了用来获取车辆载荷信息的悬架载荷测量装置,其结构主要包括车体连接板、拉线位移传感器、连接钢丝、过载保护机构总成、后轴钢板弹簧连接板、机构紧固装置。其总体结构及安装位置如图6所示,过载保护机构总成通过连接钢丝与拉线位移传感器连接,再由机构紧固装置安装在车体连接板和钢板弹簧之间。悬架特性检测装置车辆加载时,由于载荷作用车架与车桥产生相对位移,传感器拉线的伸缩量也随之发生改变,拉线位移传感器可将机械位移量转换成可计量的、成线性比例的电信号,利用拉线传感器的性质测量车辆不同装载量时输出的电压值,建立车辆各轮胎垂向载荷与拉线式位移传感器输出电压间的关系。
采用解放牌赛龙载货汽车作为试验车辆搭建车辆载荷状态监测预警系统,使用飞思卡尔16位单片机作为车载终端进行数据采集和预处理,使用C++语言编写数据采集预处理程序,数据通过车载终端计算机中基于LABVIEW编写的程序对载荷状态信息进行处理显示。系统的搭建及试验现场如图7所示:
车辆在行驶过程中,由于路面不平、发动机振动,轮胎驱动力等影响会给传感器施加若干频率和振幅的叠加作用力,影响装置对车辆装载状态的判断,使用EMD方法对载荷电压信号进行去噪处理可以有效剔除载荷电压信号中的动态成分。
EMD的原理是将信号分解成不同频率的表征信号IMF,分解后的原始信号x(t)可表示为
x(t)= 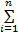
式中: 
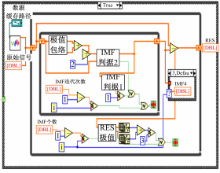
将信号中的动态量滤除,得到稳态载荷 r n( t)。 EMD分解的方法参照文献[10]。经过对大量载荷数据的分析处理,可找到最佳处理效果的 EMD分解参数并采用镜像拓延法抑制端点效应。基于 LabVIEW软件开发了 EMD处理程序,其程序主 IV图如图8所示:
包括极值包络, IMF判据1、2和筛分终止条件等子 IV模块,程序完成了对载荷数据的导入、去噪、分析,最终在计算机上显示处理结果。
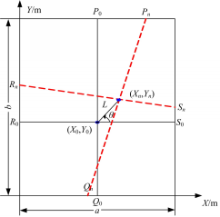
如图9所示的车辆坐标系中,将左后侧传感器固定位置定义为坐标系原点,当车辆加载均匀时质心为( X1, Y1)。
车辆在行驶过程中四个轮位安装的拉线式位移传感器所检测到的悬架载荷为F1,F2,F3,F4假定货车轴长为a,货车前后轴距为b,由力矩平衡定理得:F1xp=F2·(a-xp)(9)根据式(9)解得Pn点坐标为( 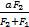
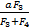
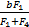
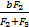
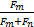
连接Pn、Qn建立直线方程,直线PnQn解析表达式为
y= 
同理得到直线RnSn的解析表达式为
y= 
联立直线PnQn和RnSn得到(Xn,Yn)的坐标为
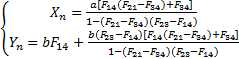 | (12) |
根据质心坐标(Xn,Yn)即可确定车辆质心位置。
质心偏移方向角为θ =arctan 
L= 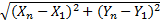
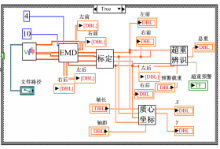
LabVIEW车辆装载状态监测程序结构如图10所示:
包括数据导入、EMD分解、载荷标定、超重辨识、质心坐标定位等子程序模块,完成载荷数据从读取、处理转换到最后结果显示的全过程。
根据悬架载荷检测装置的测量原理,需要用静态标定方法获得载荷与悬架行程即传感器测量值的关系。试验过程以0.5 t载重间隔向车上加载砝码,加载中使用CAS轴重仪测量4组轮胎的垂直载荷质量,并采集记录车载终端对应输出的4组传感器电压值,装载量为14 t时测量停止,记录28组数据,对传感器电压值与其对应的载荷数据进行二次拟合,获得标定公式如下:
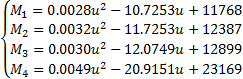 | (13) |
试验中传感器输出电压值经以上标定公式的非线性转换可得到相应的载荷值。
车辆载荷状态监测试验1以2.5 t间隔向车辆加载砝码,每一次加载使用CAS静态轴重仪测量整车质量,并且以40、60、90 km/h的速度在A级试验场路面匀速行驶,记录系统显示载荷状态数据。监测结果如图11所示:
车辆在不同车速、不同装载状态下的测量值误差均小于5%,符合系统测量要求。
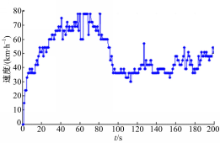
试验2的车速变化如图12所示:
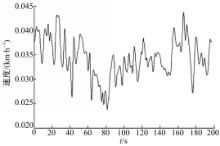
系统获得载荷数据同静态称重数据对比误差结果如图13所示:
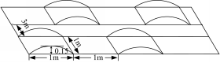
可见,与试验1相比,不同等级路面条件下车辆变速行驶的系统测量值误差范围为2%~4.5%,符合系统测量要求。车辆水平质心检测试验3在大众整车试验场稳定性测试路面(扭曲路面)上进行,装载量为5 t,扭曲路面状况如图14所示:
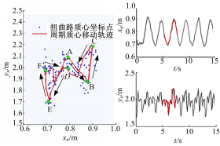
试验车驶入扭曲路段后,左右两侧车轮交替驶过以高度0.15 m,长度1 m为周期变化的扭曲路面。对车辆水平质心位置监测结果如图15所示:
选取试验过程中车辆经过扭曲路面的一个起伏周期(对应图15的A~F)的数据进行分析,试验中车辆左前轮遇扭曲路面坡度被抬起,质心向右后移A→B,左前轮下坡过程中质心向左后移C→D,随后右前轮遇扭曲路面坡度被抬起,质心向左后移D→E,右前轮下坡过程中心向右后移F→A,以此规律车辆低速行驶在扭曲路面,经历若干起伏周期,质心位置变化重复以上轨迹构成图15中左图所示散点区域。分析可知:
(1)车辆行驶在扭曲路面时,水平质心位置在载荷坐标系成蝶状散点分布。质心轨迹随着规则扭曲路面坡度变化呈周期循环往复。
(2)根据图15中右图所示的质心位置在横向和纵向坐标上的投影曲线图可以看出,质心位置随扭曲路面波形呈周期性规则变化,说明算法从定性方面上可行。
(1)建立了非独立悬架二自由度车辆1/2振动模型,以路面不平度作为激励输入MATLAB/Simulink环境下的仿真模型,通过不同工况下悬架特性的分析,得到了悬架动行程和悬架动载呈全局线性关系。
(2)基于悬架特性分析提出一种带过载保护装置的车辆悬架载荷动态检测装置,并使用EMD方法对传感器采集到的信号进行了去噪预处理。
(3)在解放赛龙载货汽车上建立车辆载荷状态监测系统平台,提出了一种车辆载荷状态监测算法,但还需对质心位置定位精度进行验证,对车辆装载状态安全阈值的确定还需进一步研究。
(4)经过道路试验验证了不同工况下系统测量误差小于5%,系统可以准确地监测车辆行驶在扭曲路面的质心位置变化,为车辆行驶过程中装载状态异常监测预警提供了新方法。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|