当前,前缘缝翼的设计依然沿用传统设计理念,且更加关注几何细节对缝翼增升作用^{[ 7, 8]}的影响及流动机理^{[ 9, 10]}。这使得不可避免地出现凹口结构,导致无法消除由此产生的声源。在自然界中,鸮类以静音飞行著称^{[ 11, 12]}。吉林大学的研究人员基于鸮类翅膀的特殊结构对NACA0015翼型进行了仿生学设计^{[ 13]},发现仿生结构可以增强翼型的气动性。

本文从仿生学的角度出发,重点构建基于长耳鸮小翼羽的没有凹口的仿生缝翼,研究仿生缝翼在增升方面的作用。

鸮翼是由羽毛、骨骼和肌肉组成。为适应飞行时变化的流场,翅膀的展向剖面之间会有一定的相对转角,意味着不同展向位置上的弦线不在同一个平面上,这与一般的人造机翼有些不同。因此,为能在实际设计中应用,人为地对鸮翼进行一定扭转来消除相对转角,并固定在平板上,然后利用三维激光扫描仪进行扫描,见图1:

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 小翼羽内收时的鸮翼的三维扫描模型Fig.1 3D Scanning model of the owl wing with retracting alula

初始的扫描结果有很多非光滑的表面,例如,由某些羽枝翘起产生的小面。对此,需要将扫描后的结果进行光顺化处理,以便消除这些奇异边界。翼尖附近的羽毛非常薄,甚至有些羽毛之间没有重叠,以致不能提取剖面,所以从翼尖到小翼羽这部分三维模型被去掉。这样,根据处理后的三维翼模型可以提取二维剖面,具体步骤如下:

(1)在小翼羽翼尖到鸮翼翼根的这段三维模型的展向等距提取20个剖面。

(2)提取各个剖面的弯度和最大厚度,而后对其进行平均化。

(3)构建基于小翼羽内收的仿生翼型。

本文使用Birnbaum-Glauert中弧线分布 z_{( c)}公式^{[ 14, 15]}:

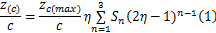
式中: η=x/c为弦线的相对坐标, x为弦线方向上的坐标; z _cmax为步骤(2)得到的平均化弯度; c为翼型的弦长:

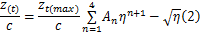
式中: z _tmax为第(2)步得到的平均化最大厚度,参数 S _n和 A _n是描绘翼型分布的多项式的系数,见表1:

表1

Table 1

表1(Table 1)

表1 中弧线和厚度分布公式中的系数 Table 1 Coefficients for the camber line distribution and the thickness distribution 系数 n=1 n=2 n=3 n=4 S n 1.503×10-1 -2.841×10-3 1.188×10-3 - A n -1.912 4.005 -3.451 1.091

表1 中弧线和厚度分布公式中的系数 Table 1 Coefficients for the camber line distribution and the thickness distribution

得到中弧线分布和厚度分布后,计算翼型剖面曲线式中: z_upper为翼型的上表面曲线的坐标; z_lower为翼型的下表面曲线的坐标。

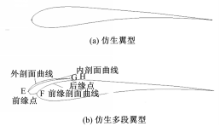
基于鸮翼的仿生翼型,即仿生缝翼内收时的仿生翼型,见图2(a):

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 仿生翼型和仿生多段翼型Fig.2 Bionic airfoil and bionic multi-element airfoil

以弦长为基准的翼型参数的相对值如下:弦长 c=100 mm,展长 l=150 mm,鸮翼模型的面积 A=15000 mm²,最大厚度 z _t(max)=14.77%,最大厚度的位置 x _zt(max)=15.00%,弯度 z _cmax=3.80%,弯度的位置 x _zcmax=50.40%。

(4)构建基于小翼羽外伸的仿生多段翼型。从工程实际出发,这里认为仿生缝翼的外剖面曲线是仿生多段翼型的一部分。进一步假定仿生缝翼与固定翼的前缘点,仿生缝翼内、外剖面曲线的起点E,固定翼前缘剖面曲线的起点F重合。随后,在三维小翼羽模型的展向中间位置上提取具有代表性的下表面曲线,然后对其进行二次曲线拟合,并作为仿生缝翼的内剖面曲线。接着,以此曲线沿着仿生翼型的前缘剖分仿生翼型,得到仿生缝翼内、外剖面曲线的终点G和固定翼前缘剖面曲线的终点H。可以发现点G既与点H重合,又是仿生缝翼的后缘点。这样就确定了仿生缝翼外伸时的仿生多段翼型,见图2(b)。可以看到仿生缝翼没有凹口,这样就有效地避免了由此产生的声源。

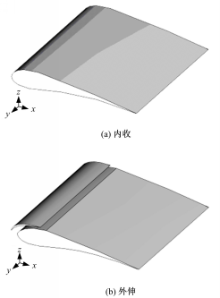
根据图2所示的二维翼型的几何参数制作准二维的仿生缝翼内收和外伸的试验模型。对于仿生翼型的准二维模型参数如前文所述,而对于仿生多段翼型,内收时的展长和弦长分别为150 mm和100 mm,但还需仿生缝翼的位形参数,以仿生多段翼的弦长为基准的相对参数值如下:弦长值为25%,前伸值为5%,偏角为0°,下垂值为1%,,缝道值为0.925%。这里采用快速成型系统制作准二维试验模型,见图3:

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 仿生缝翼内收和外伸时的准二维仿生模型Fig.3 Quasi-2D bionic models with retracting and stretching bionic slat

试验在低湍流度的LW-9117风洞中进行,试验段的界面为150 mm×150 mm。风洞测试会带来一定的尺度效应和虚假雷诺数效应,本文的二元试验采用洞壁干扰修正,即浮力修正,固体阻塞修正,尾流阻塞修正和流线弯曲修正。使用的修正公式如下:

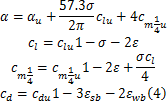
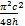
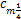
式中: ε为阻塞修正因子, ε=ε_sb +ε_wb, ε_sb为固体阻塞修正因子, ε_wb为尾流阻塞修正因子; σ= 为流线弯曲修正因子, c为模型弦长, h为风洞高度; α、 c_l、 、 c_d分别为攻角、升力系数、力矩系数和阻力系数,其中下标中有u的表示原始数据,没有u的表示修正后的数据。

根据使用的风洞的尺寸和翼型几何外形计算得出

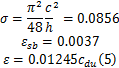
同时,用模型将翼型和三向测量单元之间的链接件覆盖,以便忽略链接件的气动力,这样就能得到风洞修正后的数据。本文还通过烟线显示绕翼流动,证实仿生缝翼内收和外伸时导致的不同气动升力提供相应的流场结构,以便揭示仿生缝翼对流场影响的机理。

自然界中鸮降落时的雷诺数 Re一般不超过6×10⁴,并且飞机降落时也处于低雷诺数状态,因此这里选择的试验速度为5.9、8.8 m/s,相应地,雷诺数分别大约为4×10⁴和6×10⁴。图4是不同雷诺数下仿生缝翼内收和外伸时的升力系数曲线。从图中可以看到,仿生缝翼处于不同的状态会对升力系数曲线的变化有以下较大的影响。

图4

Fig.4

	Figure Option ViewDownloadNew Window
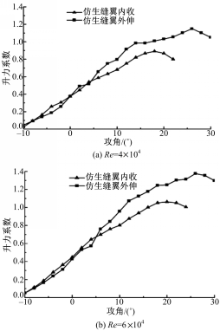	图4 在 Re=4×104和6×104情况下随攻角变化的升力系数分布Fig.4 Distribution of the lift coefficient over angles of attack for Re=4×104 and 6×10

⁴(1)在攻角小于5°时,仿生缝翼外伸会降低升力系数。此时,仿生缝翼的弦向与气流的流向之间的夹角较大,从而导致仿生缝翼的迎风面较大,像机翼上的扰流器一样工作,起到减小升力和增大阻力的作用。同样,鸮在小攻角飞行时小翼羽也是内收的。

(2)攻角大于5°时,仿生缝翼外伸有助于升力系数的提高,并且随着攻角的变大仿生缝翼的作用也变明显。此时仿生缝翼起到前缘缝翼的作用,可以在低雷诺数下提高翼型整体的升力。类似地,鸮只会在降落等大攻角情况下外伸小翼羽。

(3)仿生缝翼外伸可以提升仿生多段翼型的失速角和最大升力系数,见表2:

表2

Table 2

表2(Table 2)

表2 仿生缝翼内收和外伸的气动性能 Table 2 Aerodynamics with retracting and stretching bionic slat 性能指标 Re=4×104 Re=6×104 内收 外伸 内收 外伸 失速攻角/(°) 18 26 20 27 最大升力系数 0.9 1.19 1.09 1.39 斜率变化的攻角/(°) 5 14 5 18

表2 仿生缝翼内收和外伸的气动性能 Table 2 Aerodynamics with retracting and stretching bionic slat

从表中可以看到,在 Re=4 ×10⁴时,仿生缝翼内收的模型的最大升力系数只有0.9,而仿生缝翼外伸的模型的升力系数则达到了1.19,增幅达到32.2%。显然,这对翼型的整体升力有很大帮助。由于鸮类在捕食过程中滑行的角度非常陡,一般为24°,而仿生缝翼内收时的失速角为18°,所以需要仿生缝翼外伸,此时的失速角为26°。同样,在 Re=6 ×10⁴时也有类似的情况,而且随着流速的增加,相应的失速角和最大升力系数也有增长。

(4)图4中的升力曲线的斜率均有明显下降,这是由于翼型的前缘分离所致。从表2中可以看到,在 Re=4×10⁴时,仿生缝翼内收时的斜率变化的攻角为5°,而仿生缝翼外伸时则将斜率变化的攻角提高到14°。也就是说前缘附近的层流分离被延迟了9°,增加180%,加强了仿生多段翼型在相对宽的攻角下的飞行性能。同样,在 Re=6×10⁴时,仿生缝翼内收时的斜率变化的攻角为5°,而仿生缝翼外伸时斜率变化的攻角则提高到了18°,甚至比低雷诺数下的攻角还多4°。对于低速大攻角滑行的鸟类来说,这显然是非常有利的。由于在鸮类的飞行过程中小翼羽是连续变化的,而试验中的仿生缝翼是固定的,未能阻止前缘分离的发生,导致升力曲线的斜率下降。

为揭示仿生缝翼对流场结构的影响,结合仿生缝翼内收和外伸时的烟线变化情况分析其对绕翼流动的作用。图5(a)给出了仿生缝翼内收时的流场。从图中可看到,即便在较小的攻角下,由于层流边界层不能承受较大的逆压梯度而发生分离。在下游,分离气泡和自由流间的剪切层具有一定的速度梯度,造成流动的不稳定性,导致剪切层流动的转捩。卷起的湍流剪切层与壁面之间进行能量交换后,壁面附近的流体再次得到一定的速度,从而实现了再附着,这符合图4(a)中显示的气动特性。相反,图5(a)则显示仿生缝翼外伸时不会出现前缘层流分离。这可能是因为仿生缝翼与固定翼之间的缝道逐渐变小,从而产生了一个顺压梯度。同时在仿生缝翼后缘的尾流中有Kelvin-Helmholtz(K-H)不稳定性,促进下游边界层的转捩。这样边界层具有更高的流速,从而抵抗势流产生的逆压梯度和由固体表面产生的摩擦阻力。如果将仿生缝翼和固定翼看成一个整体,则仿生缝翼可被认为增加了仿生多段翼的弦长,使固定翼上表面的流速相对下降,这样产生一个相对小的压力峰和逆压梯度。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 在 α=6°和 Re=4×104情况下仿生缝翼内收和外伸时的流场Fig.5 Flow field around the wing with retracting and stretching bionic slat at α=6°and Re=4×104

(1)在小攻角的情况下,内收的仿生缝翼有碍于升力特性,起到扰流器的作用。

(2)在大攻角的情况下,外伸的仿生缝翼有利于升力系数的提高,起到前缘缝翼的作用。

(3)仿生缝翼可以提升翼型的失速角和最大升力系数。

(4)仿生缝翼能延迟升力系数曲线斜率的下降。同时绕翼烟线显示,仿生缝翼内收时出现了前缘分离,而外伸时则没有。这可能是因为逐渐缩小的缝道创造了一个顺压梯度;仿生缝翼的外伸相当于增加了仿生多段翼的弦长,减小固定翼上逆压梯度的峰值;仿生缝翼的尾流为固定翼上表面的边界层的转捩提供了扰动和不稳定性。