引用本文
王蜜, 蔡中义, 李明哲, 王大明. 三维曲面件辊压成形弯曲变形的计算及数值模拟. 2014, 44(2): 404-408[WANG Mi, CAI Zhong-yi, LI Ming-zhe, WANG Da-ming. Calculation of bending deformation of flexible roll forming for three-dimensional surface parts and numerical simulation. 吉林大学学报(工学版), 2014, 44(2): 404-408]  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
三维曲面件辊压成形弯曲变形的计算及数值模拟
王蜜, 蔡中义, 李明哲, 王大明
吉林大学 辊锻工艺研究所,长春 130022

王蜜(1987),女,博士研究生.研究方向:材料加工与数值模拟.E-mail:wangmi3214@126.com

基金:国家自然科学基金项目(51275202,51075186);
摘要

建立了有限元模型,对辊压成形过程进行模拟。基于对辊压成形弯曲变形过程的分析,建立成形件纵向曲率的计算公式,给出横截面上高度差及横截面上压缩率差的设计方法,通过有限元模拟证明了曲率计算公式的准确性。研制小型实验装置对辊压过程进行实验,通过实验验证了辊压成形可有效成形三维曲面件。

关键词: 材料合成与加工工艺; 三维曲面; 轧制; 柔性辊
中图分类号:TG306 文献标志码:A 文章编号:1671-5497(2014)2-404-5
Calculation of bending deformation of flexible roll forming for three-dimensional surface parts and numerical simulation
WANG Mi, CAI Zhong-yi, LI Ming-zhe, WANG Da-ming
Roll Forging Research Institute, Jilin University, Changchun 130022, China
Fund:
Abstract

Finite element model was proposed to simulate the flexible roll forming process. Based on theoretical analysis of bending process, the longitudinal curvature equations of the formed part was set up. The method to design maximum height difference and the compression ratio difference in the cross-section was given. Numerical simulation was carried out, and the simulation results are in good agreement with the theoretical values. A small experimental device was developed and flexible roll forming tests were carried out. The results demonstrate that flexible roll forming can be used for forming three-dimensional surface parts efficiently.

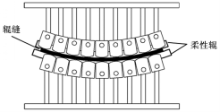
Keyword: material synthesis and processing technology; three-dimensional surface; rolling; flexible roll
引言

用连续成形方法加工三维曲面件,由于是线接触方式,所需成形力小,因而设备结构简单、投资较少,并且非常适用于加工大型三维曲面件[ 1, 2]。增量滚弯成形[ 3, 4, 5]是由Yoon等人提出的曲面成形方法,以上、下各三列滚作为成形工具,每列滚由若干短滚组成,每个短滚的位置可以调节,利用每列滚的曲线轮廓实现横向弯曲变形,由于板料的变形以弯曲变形为主,因此,成形件回弹量很大[ 6]。李明哲等[ 7, 8]将弯辊成形与轧制成形相结合提出辊压成形方法,并对辊压成形过程进行力学分析,建立了弯曲变形的计算方法与辊缝的设计方法[ 9, 10]。辊压成形以上、下两个柔性辊作为成形工具,柔性辊在自由状态下为直辊,成形时自身可以弯曲并且可以传递转矩。柔性辊上有一系列控制点,可以用来调节柔性辊形状,以构成曲线轮廓,控制板料横向变形,通过调整上、下辊辊缝的分布控制板料纵向变形,成形过程中柔性辊绕自身轴线旋转,使板料连续成形。与连续柔性成形方法相比,辊压成形回弹量小,可以获得尺寸更加精确的成形件。

通过辊压成形过程的弯曲变形分析,可以得到成形件纵向曲率的计算公式[ 7]。本文通过有限元方法模拟不同条件下辊压成形过程,对弯曲曲率公式进行验证。在成形前可利用公式计算出成形不同形状三维曲面件时的柔性辊形状及辊缝大小。

1 基本原理

辊压成形方法加工三维曲面件不需要模具,只需要两个柔性辊。通过控制上、下柔性辊的辊缝分布,使板料在沿垂直于轧制方向产生弯曲变形的同时,在板料厚度方向不均匀减薄,从而导致沿轧制方向的弯曲变形。

辊压成形参数设置时只需确定柔性辊形状及辊缝大小即可。柔性辊的形状根据成形件横向目标曲率调整,辊缝大小根据纵向目标曲率计算得到。改变柔性辊形状及辊缝大小可成形不同形状三维曲面件。辊压成形参数设置简单,可以有效实现三维曲面件成形。

图1 辊压成形装置示意图Fig.1 Principle of flexible roll forming

图1为辊压成形原理[ 8, 9],成形工具为上、下两个柔性辊,通过控制柔性辊上一系列控制点的竖直位置调节柔性辊曲率,并且在成形过程中柔性辊的形状保持不变。成形前通过调整辊缝大小控制成形件纵向变形。成形过程中,柔性辊转动,板料局部双向弯曲所产生的塑性变形不断积累,最终成形所需要的三维曲面件。

2 曲面成形控制理论与方法
2.1 曲面成形机制

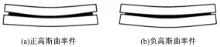
辊压成形时,上、下柔性辊之间的辊缝是不均匀的,在同一横截面上板料的不同点处厚度方向产生的压缩变形不同,从而导致纵向延伸量的不同。如图2所示:

图2 上、下柔性辊辊缝分布Fig.2 Gap distribution between the upper and lower flexible roll

辊缝中间薄两边厚时,中间部分纵向延伸量大,成形件形状为正高斯曲率件;辊缝两边薄中间厚时,两边部分纵向延伸量大,成形件为负高斯曲率件。

2.2 弯曲变形计算

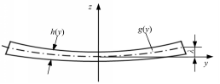
辊压成形三维曲面件截面形状如图3所示:

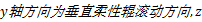
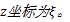
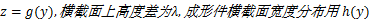
图3 三维曲面件截面形状Fig.3 Cross-section shape of three-dimensional surface

轴方向为曲面厚度方向。由于辊压成形过程塑性变形很大,因此计算时忽略材料的弹性变形,其截面几何形状与辊缝一致。出口端板料绕中性轴转动,中性轴的 成形件中线函数表示为 表示。

由于厚度方向与宽度方向相比尺寸很小,因此忽略宽展变形。根据塑性变形体积不变原则,经过成形区变形后,成形件纵向应变可表示为

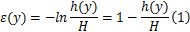
式中: 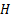为板料的原始厚度。

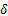
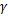
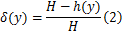
定义压缩率 为厚度压缩量与原始厚度的比值。板料边缘与中心的压缩率之差为 。

曲面成形其变形可以分解成膜变形和纵向变形两部分。膜变形为面内变形,膜变形值为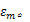

成形件纵向变形是面外变形,成形时成形件绕中性轴旋转,纵向弯曲应变可表示为

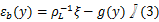
式中: 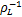为成形件纵向曲率。

辊压成形应变近似值为

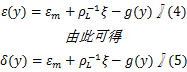
根据上述公式可得纵向弯曲变形公式[ 7]为

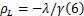
通过横截面上高度差及压缩率差值即可求成形件纵向曲率。

3 有限元模拟与分析
3.1 有限元模型

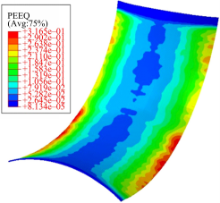
采用商业有限元软件ABAQUS对辊压成形过程进行模拟。由于隐式迭代算法在分析大变形接触问题时不易收敛[ 11],模拟时采用显式动力学算法。有限元模型如图4所示:

图4 柔性辊轧过程数值模拟Fig.4 Finite element model of flexible roll forming

上、下柔性辊均设置为刚体,根据成形件横向目标曲率半径调整柔性辊曲率半径,根据成形件纵向目标曲率半径通过式(6)计算并调整辊缝大小。材料弹性模量 E=207 GPa,泊松比 μ=0.29;密度 d=7845 kg/m2板料长度 L=0.2 m,宽度 T=0.13 m、厚度 H=0.001 m。

3.2 模拟结果

如果压缩率差 辊缝中间薄两边厚时,纵向曲率 成形后成形件为正高斯曲率件。图5为正高斯曲率成形件等效塑性应变分布,成形件中间减薄量大,两边减薄量小,与弯曲变形基本原理一致。

图5 正高斯曲率成形件塑性应变Fig.5 Plastic strain of positive gauss surface parts

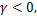
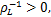
在高度差相同的情况下,对不同压缩率差的辊压成形过程进行模拟,模拟结果见表1:

表1 相同高度差时正高斯曲率件模拟结果 Table 1 Simulation results under same maximum height in the cross-section in positive gauss surface parts

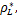
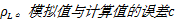
根据模拟时高度差及压缩率差值,利用式(6)计算得到纵向曲率半径计算值 根据模拟结果得到模拟值

为根据表1,纵向曲率半径模拟值与计算值平均误差为5.28%,误差较小。同时对压缩率差相同、高度差不同的成形过程进行模拟,模拟结果见表2:

表2 相同压缩率差正高斯曲率件模拟结果 Table 2 Simulation results under same compression ratio in the cross-section in positive gauss surface parts

模拟值与计算值平均误差为6.42%,说明用式(6)可以对成形件形状进行估计。

图6 负高斯曲率成形件塑性应变Fig.6 Plastic strain of negative gauss surface parts

如果压缩率差 γ>0,辊缝两边薄中间厚时,纵向曲率 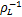<0,成形后成形件为负高斯曲率件。图6为负高斯曲率成形件等效塑性应变分布,成形件两边减薄量大,中间减薄量小。

在高度差相同的情况下,对不同压缩率差的辊压成形过程进行模拟,模拟结果见表3:

表3 相同高度差时负高斯曲率件模拟结果 Table 3 Simulation results under same maximum height in the cross-section in negative gauss surface parts

模拟结果与计算结果平均误差为11.34%。对压缩率差相同、高度差不同的成形过程进行模拟,模拟结果见表4:

表4 相同压缩率差时负高斯曲率件模拟结果 Table 4 Simulation results under same compression ratio in the cross-section in negative gauss surface parts

模拟值与计算值平均误差为6.12%。从模拟结果可以看出,正高斯曲率成形件成形精度较高,负高斯曲率成形件成形精度相对较低,但是均在可以接受的误差范围内。从以上模拟结果可以看出,用式(6)可以对辊压成形件纵向形状进行预估,也可在成形前根据所需成形件纵向形状选择合适的横截面上高度差和压缩率差值。

4 实验验证

在自主研发的辊压成形设备(如图7所示)上进行了实验,图8为成形实验件,成形件成形效果良好并没有出现褶皱、鼓包等缺陷。

图7 辊压成形设备Fig.7 Experimental setup of flexible roll forming

图8 辊压成形实验件Fig.8 Experiment parts of flexible roll forming

5 结束语

辊压成形将可弯辊与轧制技术相结合,可连续、高效加工三维曲面件。成形件形状通过柔性辊形状及辊缝分布控制。成形件横向曲率与柔性辊曲率一致,纵向曲率为横截面压缩率差与高度差的比值。实验表明,采用辊压成形方法可获得比较好的成形效果。

The authors have declared that no competing interests exist.

参考文献
[1] 李明哲, 胡志清, 蔡中义, 等. 自由曲面工件多点连续成形方法[J]. 机械工程学报, 2007, 43(12): 155-159.
Li Ming-zhe, Hu Zhi-qing, Cai Zhong-yi, et al. Method of multipoint flexible forming for the freeform surface parts[J]. Journal of Mechanical Engineering, 2007, 43(12): 155-159. [本文引用:1] [CJCR: 0.544]
[2] Cai Zhong-yi, Li Ming-zhe, Lan Ying-wu. Three-dimensional sheet metal flexible forming process based on flexible roll bending: principle and experiments[J]. Journal of Materials Processing Technology, 2012, 212(1): 120-127. [本文引用:1] [JCR: 1.953]
[3] Yamashita I, Yamakawa T. Apparatus for forming plate with a double-curved surface[P]. United States Patent: 4770017, 1988-09-13. [本文引用:1]
[4] Yoon S J, Yang D Y. An incremental roll forming process for manufacturing doubly curved sheets from general quadrilateral sheet blanks with enhanced process features[J]. CIRP Annals-Manufacturing Technology, 2005, 54(1): 221-224. [本文引用:1] [JCR: 2.251]
[5] Shim D S, Yang D Y, Kim K H, et al. Numerical and experimental investigation into cold incremental rolling of doubly curved plates for process design of a new LARS (line array roll set) rolling process[J]. CIRP Annals-Manufacturing Technology, 2009, 58(1): 239-242. [本文引用:1] [JCR: 2.251]
[6] 谷瑞杰, 杨合, 詹梅, 等. 弯曲成形回弹研究进展[J]. 机械科学与技术, 2005, 24(6): 653-658.
Gu Rui-jie, Yang He, Zhan Mei, et al. A review of the research on springback in bending[J]. Mechanical Science and Technology for Aerospace Engineering, 2005, 24(6): 653-658. [本文引用:1] [CJCR: 0.3324]
[7] Cai Zhong-yi, Li Ming-zhe. Principle and theoretical analysis of continuous roll forming for three-dimensional surface parts[J]. Science China-Technological Sciences, 2013, 56: 351-358. [本文引用:3]
[8] 李明哲, 蔡中义, 李任君, 等. 基于弯曲辊轧制的曲面零件连续成形方法[J]. 机械工程学报, 2012, 48(1): 44-49.
Li Ming-zhe, Cai Zhong-yi, Li Ren-jun, et al. Continuous forming method for three-dimensional surface parts based on the rolling process using bended roll[J]. Journal of Mechanical Engineering, 2012, 48(1): 44-49. [本文引用:2] [CJCR: 0.544]
[9] 蔡中义, 李明哲. 三维曲面连续辊压成形的力学机制及弯曲变形的计算[J]. 机械工程学报, 2013, 49(2): 35-41.
Cai Zhong-yi, Li Ming-zhe. Mechanical mechanism of continuous roll forming for three-dimensional surface parts and the calculation of bending deformation[J]. Journal of Mechanical Engineering, 2013, 49(2): 35-41. [本文引用:2] [CJCR: 0.544]
[10] 李任君, 李明哲, 薛鹏飞, 等. 板材曲面柔性轧制方法[J]. 吉林大学学报: 工学版, 2013, 43(6): 1529-1535.
Li Ren-jun, Li Ming-zhe, Xue Peng-fei, et al. Method of flexible rolling for surface sheet metal[J]. Jounral of Jilin University(Engineering and Technology Edition), 2013, 43(6): 1529-1535. [本文引用:1]
[11] Park J J, Oh S I. Application of three dimensional finite elements analysis to shape rolling process[J]. Journal of Engineering for Industry, 1990, 112(1): 36-46. [本文引用:1]