引用本文
庄蔚敏, 曹德闯, 叶辉. 基于连续介质损伤力学预测7075铝合金热冲压成形极限图. 2014, 44(2): 409-414[ZHUANG Wei-min, CAO De-chuang, YE Hui. Prediction of FLD for AA7075 under hot stamping based on continuum damage mechanics. 吉林大学学报(工学版), 2014, 44(2): 409-414]  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于连续介质损伤力学预测7075铝合金热冲压成形极限图
庄蔚敏, 曹德闯, 叶辉
吉林大学 汽车仿真与控制国家重点实验室,长春 130022

庄蔚敏(1970),女,教授,博士生导师.研究方向:车身结构设计与优化,有限元分析和金属成形技术.

基金:国家自然科学基金项目(51075178); 上海市复杂薄板结构数字化制造重点实验室开放基金项目(2013001);
摘要

针对应用试验方法获得的7075-T6铝合金板材热冲压成形极限图(FLD)的局限性,开展了基于连续介质损伤力学预测7075铝合金热成形FLD的方法研究。提出应用一组单轴黏塑性损伤本构方程并优化材料常数,建立了平面应力损伤本构方程,通过分析7075铝合金在不同温度时成形极限曲线(FLC)的特点,得出不同应力状态对损伤的影响,预测7075-T6铝合金板材在四组温度和三组应变率下的FLC。研究结果表明,基于单轴损伤本构方程进行数值分析得到的应力-应变曲线与试验曲线基本吻合。应用平面应力黏塑性损伤本构方程能够预测铝合金板材热冲压过程中不同温度和应变率的FLD,为铝合金板材热冲压过程提供失效判断依据。

关键词: 材料合成与加工工艺; 固体力学; 本构方程; 7075铝合金; 成形极限图; 热冲压
中图分类号:TG146 文献标志码:A 文章编号:1671-5497(2014)2-409-6
Prediction of FLD for AA7075 under hot stamping based on continuum damage mechanics
ZHUANG Wei-min, CAO De-chuang, YE Hui
State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China
Fund:
Abstract

In view of the limitation of the Forming Limit Diagram (FLD), which is used to evaluate the formability of AA7075 under hot stamping conditions, the continuum damage mechanics was introduced into the prediction of the FLD. A set of uniaxial damage constitutive equations was presented and the material constants were optimized. Based on the analysis of the features of Forming Limit Curves (FLCs) for AA7075 at different temperatures, a plane-stress damage equation was proposed to take account of the damage of material at different stress-strain state. Then the FLCs were predicted on the condition of four sets of temperatures and three sets of strain rates. The results indicate that the stress-strain curves of the numerical analysis of uniaxial damage constitutive equation and the experimental curves are basically consistent. Using the plane-stress unified viscoplastic damage constitutive equations can predict the FLD at different temperature and strain rate in the hot stamping process and provide the failure criteria.

Keyword: materials synthesis and processing technology; solid-state mechanics; constitutive equation; 7075 aluminum alloy; forming limit diagram; hot stamping
0 引 言

近年来,由于汽车轻量化设计需求,铝合金冲压结构件在车身上的应用不断增加。铝合金具有较高的比强度和比刚度,密度较小等优点[ 1],但在室温时成形性较差,难以使用冷冲压工艺成形结构复杂的车身结构件[ 2]。对于铝合金在室温下成形性较差的问题,一种解决办法是采用温/热成形[ 3]。随着温度的增加,成形速率降低,可以明显提高铝合金的塑性,从而生产出形状复杂的零部件。金属零部件成形时的成形能力通常用成形极限图(Forming limit diagram,FLD)来评价[ 4]。FLD试验数据是根据标准试验[ 5]获得的。高温条件下,金属材料表现为黏塑性,板材成形性与温度和应变率相关,使用试验方法获得FLD需要测得多组数据才能判断金属板材的成形极限,成本高,过程繁琐。进行材料高温FLD试验时,高温不仅影响试验模具的正常工作,还会使润滑剂出现挥发、干涸和积碳等现象[ 6],试验难以实施。目前7075-T6铝合金FLD试验的最高温度仅为250 ℃[ 2],需要对铝合金高温FLD进行预测研究,满足铝合金高温成形分析的需要。Mohamed进行了6082铝合金热冲压时的成形性预测研究[ 7],建立基于单轴应力状态的连续介质黏塑性本构方程,但是没有考虑平面应力状态对成形损伤的影响,不能用于铝合金高温FLD预测。

本文以7075-T6铝合金板材为研究对象,提出应用一组单轴损伤本构方程,基于单轴拉伸试验数据,结合多目标遗传优化算法,确定7075铝合金单轴损伤本构方程的材料常数。在单轴本构方程的基础上,通过分析最大主应力、静水应力和等效应力对损伤的影响,扩展建立平面应力黏塑性损伤本构方程。采用该平面应力本构方程预测铝合金板材热冲压时的FLD,为判断板材失效提供依据。

1 FLD特点

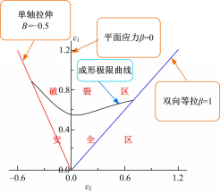
成形极限图(FLD)是板料在不同应变路径下的局部失稳极限应变(工程应变或真实应变)构成的条带形区域或曲线,表示板料在不同应变状态作用下的变形极限,如图1所示:

图1 成形极限图Fig.1 Forming limit diagram

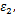
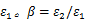
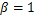
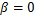
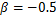
图1中,横坐标为最小主应变 纵坐标为最大主应变 为应变比率。 时为双向等拉状态; 时为平面应变状态; 时为单轴拉伸状态。成形极限曲线(Forming limit curve,FLC)下方区域为安全区,上方区域为破裂区。在板材成形过程中,若极限应变点坐标在FLC的上方,则板材失效。

2 单轴拉伸试验

7075铝合金属于超强铝合金,将其应用在汽车安全碰撞件上,在满足相同力学性能的条件下,可以明显提高汽车轻量化效果,具有广泛的应用前景。其化学成分如下:

w(Si)=0.4%, w(Fe)=0.5%,

w(Cu)=1.2%~2.0%,

w(Mg)=2.1%~2.9%,

w(Zn)=5.1%~6.1%,

w(Ti)=0.2%,

w(Cr)=0.18%~0.28%,

w(Mn)=0.3%, w(other)=0.15%。

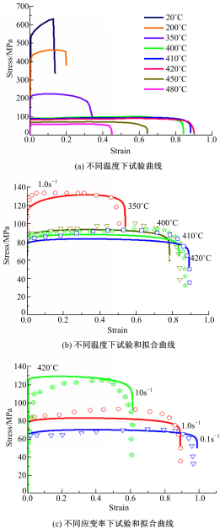
试验材料采用厚度为2 mm的7075-T6铝合金板材。试验参考中华人民共和国标准《金属高温拉伸试验方法》(GB/T 4338-2006)[ 8]的有关规定,采用Gleeble 3800热模拟试验机对板材进行单向拉伸试验,以获得不同温度和应变率下的应力-应变曲线。本研究进行的7075-T6铝合金板材单向拉伸试验结果表明,该材料的成形性能在420 ℃时为最佳,如图2(a)所示:

图2 试验应力-应变曲线与拟合曲线Fig.2 Experimental and computed stress-strain relationships for 7075

3 基于连续介质损伤力学的联立

本构方程

3.1 单轴损伤本构方程

许多国外学者已经对黏塑性本构方程进行了大量研究,模拟了一系列与时间有关的现象,例如蠕变[ 9],再结晶[ 10]和回复[ 11]等。Lin和Dean[ 12]提出基于位错硬化的本构方程,研究了热成形过程中由于回火和再结晶引起的位错回复。基于上述工作基础,并参考文献[7]中6082铝合金的本构方程,通过分析7075铝合金的力学特性,本文提出应用一组联立的单轴黏塑性损伤本构方程:

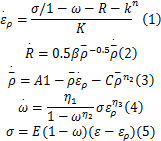
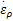
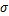
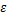
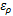
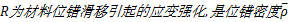
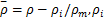
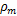
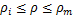
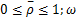
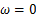
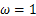
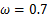
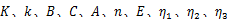
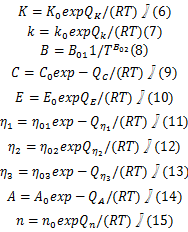
式中: 为等效塑性应变率; 为应力; 和 分别为总应变和塑性应变; 的函数; 为材料在初始状态下的位错密度, 为材料可以达到的最大位错密度,且有 ,因此 为损伤参数,变化范围是:当 时,表示材料为无损伤状态,当 时,表示材料完全损伤,通常定义当 时,材料完全失效。

参数 是与温度相关的材料常数,定义如下:

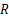
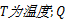
式中: 为通用气体常数; 为激活能。

3.2 本构方程参数优化

3.1节中的单轴损伤本构方程包含21个材料常数,例如 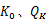等。由式(1)~(5)可以看出,本构方程是一组非线性常微分方程,各参数之间是相互耦合的,因此常规的计算方法不能求解得到材料常数。本文采用数值积分方法[ 13],通过分析试验应力-应变曲线的变化趋势,结合多目标遗传优化算法[ 14, 15, 16],使用MATLAB编写目标函数,利用Isight对目标函数进行优化计算,得到材料常数值如表1所示:

表1 7075铝合金损伤本构模型中的材料常数 Table 1 Material constants in the viscoplastic damage constitutive equations for AA7075

将所求得的材料常数值带入本构方程,基于数值分析可得到不同温度和应变率下的应力-应变曲线,如图2(b)(c)所示。经验证,拟合曲线与试验曲线基本吻合。

3.3 平面应力损伤本构方程

3.3.1 建立平面应力黏塑性损伤本构方程

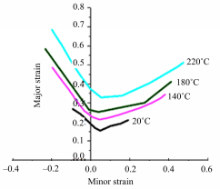
图3为7075铝合金在成形速度为5 mm/s,成形温度分别为20,140,180,220 ℃时的FLD[ 17]。从图中可以看出,曲线最低点不在平面应变轴上,随着温度的不断降低,其最低点不断向平面应变轴靠近。这是由于在热冲压过程中,不仅等效应力对损伤有影响,而且其最大主应力和静水应力也对损伤造成影响,仅仅应用单轴损伤本构方程不能准确预测铝合金的FLD。因此,基于单轴本构方程建立平面应力状态下的黏塑性损伤本构方程,如下:

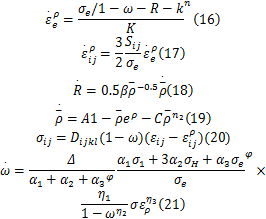
图3 7075铝合金不同温度时的FLDFig.3 The FLD of 7075 aluminum alloy at different temperatures

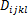
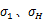
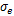
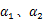
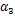
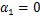
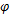
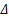
公式(20)中 为材料弹性。公式(21)是在单轴损伤公式(4)的基础上考虑不同应力状态对损伤累积的影响而推导出来的,其参数 和 分别为最大主应力、静水应力和等效应力,而 和 分别为上述应力的加权因子,表示各自应力对损伤影响的大小。例如, 表示最大主应力对损伤参数无影响。参数 为平面应力损伤指数,它表示平面应力对损伤演化的影响。参数 是单轴拉伸试验数据的修正因子。

3.3.2 确定损伤方程参数

对于平面应力问题,认为金属板沿厚度方向的应力 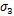为0。将平面应力损伤本构方程进行数值分析得到拟合FLC。比较试验FLC与拟合FLC,确定损伤方程(21)中的5个参数值。主要的步骤如下:

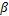
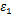
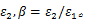
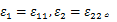
(1)根据应变率和应变比率 来定义主应变 和 如图1所示,此时,

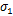
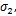
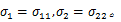
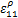
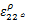
(2)采用数值分析方法求解黏塑性本构方程,通过式(20)计算主应力 和 此时, 同时计算塑性应变 和

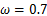
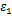
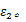
(3)当损伤因子 时,认为材料已经失效,记录此时的主应变 和

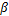
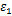
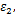
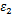
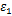
(4)通过步骤(1)~(3)来确定不同 时的主应变 和 以 为横轴, 为纵轴,得到FLC。

(5)将上述得到的FLC与试验FLC进行比较,采取多目标遗传优化算法进行优化,得到损伤方程(21)中的5个参数值。

4 计算结果与比较分析

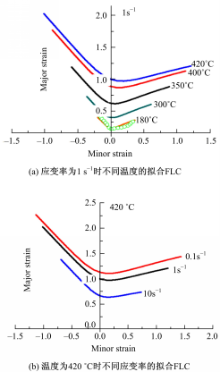
将180 ℃下的试验[ 17]FLC(图4(a)中绿色符号)与拟合的FLC(图4(a)中橙色实线)进行比较分析,采用遗传优化算法,确定损伤方程(21)中5个材料参数值为 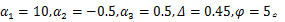采用数值积分方法,得到7075铝合金在不同温度和应变率下的FLD,如图4所示:

图4 180 ℃下的试验FLC与拟合FLCFig.4 Experimental FLC at 180 ℃ and the numerical FLC

图4(a)为当应变率为1 s-1、不同温度时的FLD。从图中可以看出,FLC的位置随着温度的升高而上升,即板材成形性能随着温度的升高而提高。

图4(b)为当温度为420 ℃、不同应变率的FLD。从图中可以看出,FLC的位置随着应变率的降低而上升,即板材成形性能随着应变率的降低而提高。

5 结 论

(1)7075铝合金板材的最佳成形温度为420 ℃。

(2)本文采用多目标遗传优化算法,计算单轴损伤本构方程材料常数。利用数值模拟方法得到7075铝合金拟合应力-应变曲线,经验证,拟合曲线与试验曲线基本吻合。

(3)建立了一组平面应力黏塑性损伤本构方程,从而预测不同温度和应变率下的FLD。从图4看出,随着温度的升高和应变率的降低,FLC的位置上升,即成形性能提高。

(4)在非等温热冲压过程中,板材的温度和应变率随着时间和位置变化很快,应用平面应力损伤本构模型能够分析任意时刻7075-T6铝合金板材热冲压过程的成形性,为铝合金板材非等温热冲压过程提供失效判断依据。

The authors have declared that no competing interests exist.

参考文献
[1] 吴晓炜, 王勇, 梁海建, 等. 铝合金覆盖件快速超塑性成形技术[J]. 塑性工程学报, 2012, 19(1): 1-5.
Wu Xiao-wei, Wang Yong, Liang Hai-jian, et al. Research on high speed superplastic forming of aluminium alloy automotive panel[J]. Journal of Plasticity Engineering, 2012, 19(1) : 1-5. [本文引用:1] [CJCR: 0.526]
[2] 黄华, 李大永, 彭颖红. 7075-T6铝合金板温热成形极限图试验[J]. 塑性工程学报, 2010, 17(1): 93-97.
Huang Hua, Li Da-yong, Peng Ying-hong. Experiment study on the foming limit diagrams(FLD) of 7075-T6 aluminum alloy sheet at warm state[J]. Journal of Plasticity Engineering, 2010, 17(1) : 93-97. [本文引用:2] [CJCR: 0.526]
[3] Wang Hui, Luo Ying-bing, Peter Friedman, et al. Warm froming behavior of high strength aluminum alloy AA7075[J]. Transactions of Nonferrous Society of China, 2012 , 22(1): 1-7. [本文引用:1] [JCR: 0.917] [CJCR: 0.7776]
[4] 林敦文, 关绍康, 卢广玺, 等. Al-Mg-Si基合金车身板材成形极限及数值应用[J]. 机械工程材料, 2006, 30(4): 64-67.
Lin Dun-wen, Gun Shao-kang, Lu Guang-xi, et al. Forming limit of Al-Mg-Si based alloy automotive outer sheet and its numerical application[J]. Materials for Mechanical Engineering, 2006, 30(4): 64-67. [本文引用:1] [CJCR: 0.2812]
[5] 全国锻压标准化技术委员会. GB/T 15825. 8-1995 金属薄板成形性能与试验方法-成形极限图(FLD)试验[S]. [本文引用:1]
[6] 朱小芸. 涂装烘干室设备的高温润滑[J]. 汽车工艺与材料, 2009(9): 37-41.
Zhu Xiao-yun. High temperature Lubricating of Coating oven equipment[J]. Automobile Technology & Material, 2009(9): 37-41. [本文引用:1]
[7] Mohamed M S, Foster A D, Lin Jian-guo, et al. Investigation of deformation and failure features in hot stamping of AA6082: experimentation and modelling[J]. International Journal of Machine Tools & Manufacture, 2012, 53(1): 27-38. [本文引用:1]
[8] 全国钢标准化技术委员会. GB/T 4338-2006金属材料高温拉伸试验方法[S]. [本文引用:1]
[9] Zhan Li-hua, Lin Jian-guo, Dean T A, et al. Experimental studies and constitutive modeling of the hardening of aluminium alloy 7055 under creep age forming conditions[J]. International Journal of Mechanical Sciences, 2011, 53(8): 595-605. [本文引用:1] [JCR: 1.613]
[10] He Yun-bin, Pan Qing-lin, Chen Qin, et al. Modeling of strain hardening and dynamic recrystallization of ZK60 magnesium alloy during hot deformation[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(2): 246-254. [本文引用:1] [JCR: 0.917] [CJCR: 0.7776]
[11] Greze R, Manach P Y, Laurent H, et al. Influence of the temperature on residual stresses and springback effect in an aluminium alloy[J]. International Journal of Mechanical Sciences, 2010, 52(9): 1094-1100. [本文引用:1] [JCR: 1.613]
[12] Lin J, Dean T A. Modelling of microstructure evolution in hot forming using unified constitutive equations[J]. Journal of Materials Processing Technology, 2005, 167(2/3): 354-362. [本文引用:1] [JCR: 1.953]
[13] Cao J, Lin J, Dean T A. An implicit unitless error and step-size control method in integrating unified viscoplastic/creep ODE-type constitutive equatio-ns[J]. International Journal for Numerical Methods in Engineering, 2008, 73(8): 1094-1112. [本文引用:1] [JCR: 2.056]
[14] Li B, Lin B, Yao X. A novel evolutionary algorithm for determining unified creep damage constitutive equations[J]. International Journal of Mechanical Sciences, 2002, 44(5): 987-1002. [本文引用:1] [JCR: 1.613]
[15] Lin J, Cheng B H, Yao X. Universal multi- objective function for optimising superplastic-damage constitutive equations[J]. Journal of Materials Processing Technology, 2002, 125-126(9): 199-205. [本文引用:1]
[16] Cao J, Lin J. A study on formulation of objective functions for determining material models[J]. International Journal of Mechanical Sciences, 2008, 50(2): 193-204. [本文引用:1] [JCR: 1.613]
[17] 王辉. 成形极限图的获取方法与其在金属板料成形中的应用[D]. 南京: 南京航空航天大学机电学院, 2011.
Wang Hui. Acquisition method of forming limit diagram and its application in sheet metal forming[D]. Nanjing: Electrical and Mechanical College, Nanjing University of Aeronautics and Astronautics, 2011. [本文引用:2]