DEM可以描述如下:任何一个基因i在时刻t的表达值导数存在如下式所示回归方程特征: 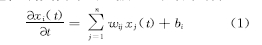式中:w_ij为网络中基因j对基因i影响的权值,所有权值构成全局矩阵 W, W是一个 N×N的方阵, N表示网络中基因节点数,网络带有方向性,所以 w _ij不等于 w _ji,其含义正好相反; x _i( t)为 t时刻下基因 i的表达浓度; b _i为基因 i的背景浓度,即无外界干扰下基因 i本身的表达浓度。

对一个有 N个基因 T个时段的时序基因表达数据,可表示为

X _N×T =

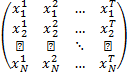(2)

式中: x表示浓度,下标为基因标识,上标为时间序号。

根据式(2),式(1)可写为

d X _N×T /d t= W _N×N X _N×T + B _N×T(3)

现将 X _N×T进行奇异值分解,得到:

X _N×T = U _N×T A _T×T

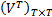(4)

在式(4)中 V与 U都是正交矩阵,而且均满足一定约束条件:

U ^T U = U ^-1 U = V ^-T V = V ^-1 V = E(5)

在式(5)中 E为单位矩阵,所以 V与 U的逆矩阵等于相应的转置矩阵。为使式(5)成立, U与 V需为广义逆矩阵^{[ 12]}。将式(3)变形并带入式(4)得到:

W _N×T =(d X _N×T /d t- B _N×T) V ^-T A ^-1 U ^-1(6)

式(6)是 GRN的一个特定解,但是此解不一定是 GRN构建所需最优解。需采取一定方法来找出最优解。从式(6)继续出发,可进一步得到算法所需取值范围,即:

W _N×T =(d X _N×T /d t- B _N×T) V ^-T A ^-1 U ^-1 +C U ^-1(7)式中: C表示任意一个常数。

式(7)是以式(6)作为特解情况下的通解结构。从数学角度讲, W的所有可能解均在公式(7)中。有了此通解后就可在这个缩小的解空间范围内进行 DEM优化求解,并最终找到稳定的 GRN。

通过SVD得到DEM通解后,即可在取值范围内进行优化和求解。需要找到一个合理的能量函数,即评价标准来规范DEM。本文采用最小二乘方法来规范这一标准:

c=

(8)

式(8)表示观察值和方程所求值之差的平方,r_ik是一种残基,具体规定如下:

r_ik=x'_i(t)- w_ijx'_j(t)-b_i(9)

式中:x'_i(t)为t时刻基因i表达值的导数,即变化率:

x'_i(t)=x_i(t)-x_i(t-1)(10)

欲采用GFA求式(8)的最小值,需要由一个权值矩阵组成一个灰尘,矩阵维度与 W相同。这是特殊形式的灰尘格式,但代入 GFA质量函数即式(8)后也应有一个标量结果,作为比较大小的标准。由于矩阵中每个元素的大小的取值范围并不确定,但是绝大多数不会超过 ±100,所以将每个元素的取值范围定为[ -100,100],则灰尘的初始化过程描述如下:

(1)在 N×T次的循环中,每次循环均赋予一个取值在[ -100,100]内的随机值,作为该矩阵灰尘相应位置的元素。

(2)随机初始化完所有 N×T个元素后,将该矩阵代入式(7)中检验是否成立,即是否能求出常数 C值,如能求出,则该灰尘在解空间范围内存在,初始化完毕,否则重新回到步骤(1)再重新初始化。

(3)重复步骤(1)(2)的过程,直到所有灰尘产生。

经过以上3步后完成 GFA的初始化阶段。可见, SVD过程所产生的结果可作为 GFA算法的灰尘取值范围,即相应的解空间,在此基础上可以减少大量不必要的计算,提高 GFA的运行效率。

解空间分解部分采用随机分配方案,因为灰尘的维度过于复杂,平均法不适合解决当前问题。移动算子部分相对特殊,采用如下过程:

(1)对周围灰尘和中心灰尘 N×T个对应元素进行比较,若周围灰尘的元素值不等于中心灰尘相应的元素值,则周围灰尘元素值向中心灰尘元素值靠近,规则采用黄金分割移动形式^{[ 11]}。

(2)进行完 N×T次元素的对比与移动后得到新的灰尘值,将新的灰尘值代入式(7)中进行验证,若满足条件即能求出相应C值,则判定移动成功,进入步骤(4),若不满足条件即求不出相应C值,则进入步骤(3)。

(3)减小移动步伐,使其变为原来的二分之一或三分之一重新进行移动,若已进行P次(P为某一常数)重新移动仍未找到合理移动,则将此周围灰尘删除,即对此周围灰尘直接吸收。

(4)计算与新灰尘值相应的质量函数值,若该值比中心灰尘质量函数值还小即更优,该新值成为新的中心灰尘,原有中心灰尘降为周围灰尘,该组内所有灰尘围绕中心灰尘重新进行移动计算。

经过以上步骤后移动算子结束,吸收算子部分采用标准形式^{[ 11]},即直接删除。至此 GFA在 GRN的应用部分改进结束。在前文所述的权值大小定义中,负值表示抑制作用,即负调控,正值表示促进作用,即正调控,0表示不存在任何调控关系。

在上面所述 GRN构建过程中,计算的是一个全连接的网络,包括节点对自身的控制。但是事实上 GRN往往不是这种密集网络,而是一种稀疏网络。解决这一矛盾的方法较多,但最直接最有效的方法仍然是阈值截取法,即设定某一阈值,比如0 .5,如果当相应权值的绝对值小于0 .5时,即正负调控的影响力小于0 .5时,将此值记为0,即删除相应影响。正负调控影响大于0 .5时,记作影响存在。

通过微分方程模型,采用 SVD缩小和确定解空间范围,运用 GFA优化网络结构,整个过程流程图如图1所示:

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 GFA进行GRN构建过程流程图Fig.1 The flow chart of GRN with GFA

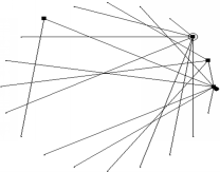
对GRN构建首先要从模拟数据出发,验证网络构建算法的准确性。模拟数据采用算法生成方式获得,首先生成遵从幂律分布的无标度网络^{[ 13]},然后采用DEM的逆向形式获得相应的基因表达数据。根据已有研究,基因调控网络中的控制节点数量很少,且任意一个节点与其他节点连接数都服从幂律分布,一个生成的典型无标度网络结构如图2所示:

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 典型无标度GRN图Fig.2 A typical scale-free GRN

在图2中,方块表示GRN调控节点,空心圆表示自调控节点,唯一的实心圆则表示节点0,逆时针顺次为节点1,2,…,19。与此相对应也模拟产生了对应的基因表达数据,部分基因表达数据如表1所示:

表1

Table 1

表1(Table 1)

表1 对应图2产生的部分基因表达数据 Table 1 Part of gene expression data of figure 2 节点 时序0 时序1 时序2 时序3 node0 0.329 0.135 0.358 0.251 node1 0.934 0.439 0.314 0.900 node2 0.911 0.708 0.627 0.600 node3 0.501 0.595 0.530 0.527

表1 对应图2产生的部分基因表达数据 Table 1 Part of gene expression data of figure 2

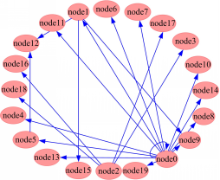
由类似表1所示的基因表达数据,通过图1流程图所示方法进行GRN构建,获得相应的权值矩阵 W,然后通过免费软件 Cytoscape^{[ 14]}进行显示,结果如图3所示:

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 基于GFA构建的模拟数据GRN图Fig.3 GRN of simulated data based on GFA

在图3中箭头表示基因间的相互影响关系,在Cytoscape中采用Circle算法^{[ 15]}进行拓扑布局,所以节点序号发生一定改变,但并不影响算法准确度和运算时间的对比。为比较GFA算法在GRN构建能力方面的优劣,本文使用GA和SA算法进行运算并与本文结果进行对比。

采用Bansal的PPV和Se函数^{[ 16]}进行计算,公式如下:

PPV=

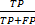(11)

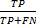
式中: TP=True Positive,表示计算结果为真,实验获得的真实值也为真; FP=False Positive,表示计算结果为假,但通过实验获得的真实值却为真; FN=False Negative,表示计算结果为真,但通过试验获得的真实值却为假。

从式(11)的定义和数学关系来看,PPV和Se都是越大越好,可以根据这两个值来判断算法准确性如何。

除准确度外算法的运算时间也是重要的对比参数。本文将GFA、GA和SA三种算法都用在GRN构建中,且均为图2所示的GRN。运算次数均为500次,将这些不同的结果各自取平均值,总结如表2所示:

表2

Table 2

表2(Table 2)

表2 三种算法分别计算GRN的结果对照表 Table 2 Compared results table of reconstruction of GRN with three algorithms 算法 PPV Se 运算时间/s GFA 0.329 0.735 2.58 GA 0.304 0.639 4.35 SA 0.286 0.595 12.90

表2 三种算法分别计算GRN的结果对照表 Table 2 Compared results table of reconstruction of GRN with three algorithms

从表2中可以看出,GFA算法在PPV和Se上都有一定的优势。运算时间上GFA算法也更快,这是因为SVD方法确定了候选解的解空间范围,加快了运算速度,同时GFA算法本身也可以运算得很快。相比较而言,GFA算法最为出色,但并未超过GA算法太多,SA算法最差,尤其是运算时间过长。

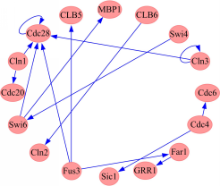
真实数据实验采用的是酵母基因表达数据GDS38,此数据可在GEO数据库获得,对应的GRN结果图可从KEGG数据库获得。本实验只取KEGG酵母GRN图中的一部分基因及其相应的基因表达数据矩阵,采用GFA算法进行GRN优化与构建。此网络子图包含16个基因,如图4所示:

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 基于GFA构建的GDS38部分GRN图Fig.4 GRN of part of GDS38 data based on GFA

图4是GFA预测的16个酵母基因的结果图,欲得到完整的有统计意义的数据结果,同样需要进行500次GFA、GA和SA的不同实验,结果如表3所示:

表3

Table 3

表3(Table 3)

表3 三种算法分别计算GDS38的GRN的结果 Table 3 Compared results table of reconstruction of GDS38 GRN with three algorithms 算法 PPV Se 运算时间/s GFA 0.286 0.658 2.36 GA 0.238 0.628 4.28 SA 0.196 0.576 11.20

表3 三种算法分别计算GDS38的GRN的结果 Table 3 Compared results table of reconstruction of GDS38 GRN with three algorithms

从表3的统计结果可以看出,GFA算法具有更高的准确性,但是与模拟数据相比准确度相对较低,这是因为模拟数据没有其他外界干扰,数据更纯,但不影响GFA与其他算法的比较。同时运算时间也比模拟数据相对要少,这是因为运算节点比模拟数据少了4个。总之,GFA算法在基因调控网络构建过程中可以起到很关键的作用,运算速度更快且运算结果更准。