刘富(1968),男,教授,博士生导师.研究方向:计算机视觉及模式识别.E-mail:liufu@jlu.edu.cn
支持向量数据描述(SVDD)是一种有效的数据描述算法。该算法中,作为定值的惩罚因子决定了数据描述的精度。然而实践中惩罚因子的选择是极其困难的,尤其是在训练数据含有噪声的情况下。为了解决这个问题,本文提出了一种可变惩罚因子的支持向量数据描述(VT-SVDD)算法。该算法根据样本点在核空间的位置分布,为每个样本计算一个惩罚因子,然后基于这种可变惩罚因子求解一个凸约束二次规划,即可以得到对数据集的球形域描述。为了验证所提的VT-SVDD的性能,在UCI数据集上进行了无噪声、有噪声两类训练数据的仿真实验。实验结果表明,VT-SVDD能有效提高传统SVDD的精确度和稳健性。
Despite the factor that Support Vector Domain Description (SVDD) model is an effective method for describing a set of training data, one inherent drawback is that the description is very sensitive to the selection of the trade-off parameter, which is hard to estimate in practice. To solve the difficulty, we proposed a novel Variable Trade-off parameter Support Vector Domain Description (VT-SVDD). In the proposed VT-SVDD, first, we assigned a position-based variable trade-off parameter to each data point. Then we computed a convex constrained quadratic programming based on the variable trade-off parameters. Finally, we can obtain a spherical data domain description for the training data. Experimental results demonstrate that the VT-SVDD can significantly improve the accuracy and robustness on UCI data sets.
SVDD(Support vector data description)是Tax等人以支持向量分类器为基础提出的一种球形数据描述算法[
目前虽然对SVDD算法已有一些研究,然而该算法仍存在一个本质缺陷,就是作为定值的惩罚因子决定着SVDD的数据描述精度,然而实践中惩罚因子的选择是极其困难的。尤其在实际应用中,采集到的训练数据往往包含噪声,这种给所有的训练数据(包含正常点和异常点)都设置相同惩罚因子的方法,并没有考虑不同数据在训练集中的差异,这在一定程度上影响了SVDD的数据描述能力。为了解决这个问题,本文提出了一种可变惩罚因子的稳健支持向量数据描述方法(VT-SVDD)。这种方法基于样本点在核空间的位置分布,为每个样本计算一个惩罚因子,然后基于这种可变惩罚因子求解一个凸约束二次规划,就可以得到对数据集的球形域描述。为了验证所提的VT-SVDD方法的性能,本文在UCI数据库中收集了8个连续数据集,在这些数据集上进行了无噪声、有噪声两方面仿真实验,实验结果表明,VT-SVDD模型提高了传统SVDD模型的精确度和稳健性。
对于一个给定数据集 X, X ={ x1, x2,…, x N},其中 x i =( x i1, x i2,…, x iM)∈R M是一个 M维的数据点,传统 SVDD方法的主要思路是求解式(1)所示的凸约束二次规划获得一些支持向量,通过这些支持向量,可以在核空间找到一个 o *为球心, r为球半径的最小超球 S( o *, r),使得该最小超球包含尽可能多的该类数据点。
 | (1) |
式中:‖·‖为2范数;φ(·)为对称的非线性映射函数;ξ i≥0为一个松弛变量;C为惩罚因子,用来表示取舍数据点的意愿,C的取值越大,表示数据集X中的那些数据点是正常点的可能性越大,舍去它们的意愿就越弱,求解式(1)获得的最小超球S(o *,r)的容积就越大,C的取值越小,表示数据集X中的数据点是异常点的可能性越大,舍去这些点的意愿就越强,求解式(1)获得的最小超球S(o *,r)的容积就越小[
综上所述,在传统 SVDD算法中,作为定值的惩罚因子 C决定着球形数据描述的大小,也决定着 SVDD对数据集描述的精度。
首先需要计算数据集 X的中值向量 μ。对于含有 N个数据点的样本集 X, X ={ x1, x2,…, x N},每个数据点 x i =( x i1, x i2,…, x iM)∈R M是一个 M维的向量。令在样本集 X中,第 j个元素的次序统计量为 x, j(1)≤ x, j(2)≤…≤ x, j( N), j∈[1, M],则对第 j个元素,当 N是奇数时,样本集的中位数为 μ j =x, j( 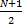



为了计算每个数据点的惩罚因子,需要计算在核空间中每个训练数据与中值 μ的空间距离向量 d,
d =[ d l
 | (2) |
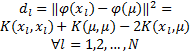
式中:K(·)为核函数,且K(a,b)=(φ(a),φ(b))。
惩罚因子 w i(∀ i=1,2,…, N)的计算公式为
w i =1 - 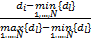
对数据集 X中的每个数据点 x i引入它的惩罚因子 w i,让可变的惩罚因子 w i取代传统 SVDD模型中的定值惩罚因子 C来描述数据集 X的特征空间域。通过解凸约束二次规划以获得包含最多数据点的最小超球
:
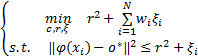 | (4) |

L(o *,r,α i,β i,ξ i)=r2+ 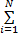


在拉格朗日乘子 α i≥0和 β i≥0的条件下,对拉格朗日函数中的每个变量求偏导,并令其等于0,对∀ i=1,2,…, N,新的约束条件变为
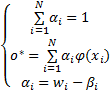 | (6) |
因为 α i≥0和 β i≥0,将变量 β i从式(6)的第三个约束中移除,则 α i =w i -β i变成 w i≥ α i≥0这样一个约束条件。
由 KKT互补条件可得:
 | (7) |
重写式(5)可以获得式(4)的对偶函数如下:
 | (8) |
值得注意的是,拉格朗日乘子α i,∀i=1,2,…,N的上边界不再被相同的惩罚因子C决定,而是每个α i被对应的可变惩罚因子w i控制着。基于可变惩罚因子的一个负面影响就是增强了核参数对分类结果的影响,因为不仅计算惩罚因子,而且拉格朗日乘子的上边界都依赖于所选的核参数。
根据拉格朗日乘子 α i的值和其对应的惩罚因子 w i,∀ i=1,2,…, N,数据集 X中的数据点可分为以下三类:
(1)球内向量( IP): α i =0,则数据点 x i在超球面内部。因为已知 α i =w i -β i且 β i ξ i =0,又因为 α i =0,可推导出 ξ i =0。因此, 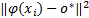
(2)支持向量( SV):0 <α i 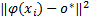
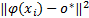
(3)球外向量( OP): α i =w i,则数据点 x i在超球面外部。由于 α i =w i -β i且 β i ξ i =0,由 α i =w i可推导出 ξ i≥0。又根据 α i( 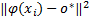
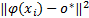
根据计算所获得的这些支持向量,就可以获得一个包含最多正常数据的超球 S( o *, r), S( o *, r) ={ x i 
半径 r可定义为 r=mean{ 
为获得较好的分类结果,本文选择高斯核函数 K G( x i, x j) =exp[ -q 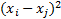
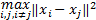
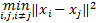
用符号函数 f来决定是否数据点 x i属于数据集
X。 f=sign( r2 - 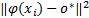
这里有两种情况:①如果新数据点在核空间的像φ( x i)落在超球内部或超球面上,即是 f=1或 f=0,则认为新数据点 x i是正常点,属于数据集 X。 ②如果新数据点在核空间的像 φ( x i)落在超球外部,即是 f=-1,则认为新数据点 x i是异常点,不属于数据集 X。
为了验证 VT-SVDD算法的性能,本文从 UCI数据库[
| 表1 数据集描述 Table 1 Summary of data sets |
在这些数据集上,进行了两个方面仿真实验来验证分类模型的性能:一个实验是在 UCI数据库收集的原始数据集上进行;另一个实验是在原始的 UCI数据集中加入噪声,用含有噪声的数据集验证分类模型的稳健性。在这两个实验中,用分类精度作为衡量分类模型稳健性的标准,分类精度越高,代表该分类模型越稳健。在每个实验中,将VT-SVDD与4种分类方法(PSVDD、SVDD、K-NN和SVMs)进行了比较。其中VT-SVDD、PSVDD、SVDD和SVMs所选核函数均为高斯核函数,核参数q及SVDD、SVMs的惩罚因子C通过交叉验证的方法,寻找让每个方法取得最优识别率的参数[
首先,用UCI数据库中收集的原始数据集验证VT-SVDD算法的性能。以wine数据为例,先将其平均分成10份,选择其中的9份作为训练样本,余下的1份作为测试样本。然后用本文所提的VT-SVDD判断测试样本的分类类别。将这一过程重复进行10次,以保证wine中每一个数据都可以作为测试样本进行分类测试。最后,统计10次预测的精度,求取其平均值作为wine数据集的最终分类精度。数据集用各种不同的分类模型得到的分类精度见表2:
| 表2 原始数据集的分类精度 Table 2 Classification accuracies of raw data sets % |
从实验结果可以看出,在8个实验数据集中,VT-SVDD在wine和sonar数据集上的分类精度高于其他分类方法;在diabetes数据集上,VT-SVDD和K-NN共同取得71.3%的最高分类精度;PSVDD在WDBC、WPBC和iris数据集上取得的分类精度高于其他分类方法;K-NN在glass数据集上取得了最高的分类精度。总体而言,本文所提的VT-SVDD方法和PSVDD方法都能取得高于84%的分类精度,K-NN其次,能取得83.5%的分类精度,经典SVDD和SVMs的实验结果较保守,分别取得了82.1%和82%的分类精度。
为了进一步对比各种分类模型的稳健性,本文将原始的UCI数据集加入噪声,用含有噪声的数据集来验证VT-SVDD方法的稳健性。同样以wine数据集为例,先将其平均分成10份,选择其中的9份数据集并将其污染成含有 a%的类噪声的数据集,余下的1份作为测试样本。用VT-SVDD、PSVDD、SVDD、K-NN和SVMs分类方法对测试数据进行分类预测。将这一过程重复进行10次,以保证wine数据集中每一个样本都可以作为测试样本进行分类测试。这样就可以得到在噪声水平为 a%的环境下对数据集进行分类的实验结果。统计10次预测的分类精度,求取其平均值作为wine数据集的最终分类精度。
本文对8个数据集分别添加5%、10%和20%的噪声水平,然后测试各种分类模型的稳健性。数据集在不同噪声水平下的分类精度结果见表3:
| 表3 噪声数据集的分类精度 Table 3 Classification accuracies of noisy data sets % |
表3显示, 在训练数据添加噪声的情况下, VT-SVDD仍能够在wine、WDBC、WPBC、iris、和diabetes数据集上取得最好的分类精度;K-NN在iris、ionosphere、diabetes数据集上取得最好的分类精度;PSVDD和传统SVDD次之,分别在WDBC、sonar和glass数据集上取得最好的分类精度。总体而言,本文所提的VT-SVDD能取得最高的分类精度为81.1%;PSVDD、K-NN次之,分别取得80%和80.3%的分类精度;传统SVDD和SVMs也分别取得了76.6%和74.9%的分类精度。
将表3与表2的实验结果进行比较可以看出,训练数据添加噪声后,所有分类方法的分类精度都有所下降,其中VT-SVDD、K-NN的分类精度下降最为缓慢,均为3.2%;PSVDD、SVDD次之,添加噪声后分类精度分别下降了4.5%和5.5%;SVMs的分类精度下降最多,为7.1%。
图1展示了随着训练数据集中噪声的增加,各种分类方法所取得的分类精度的变化趋势。当训练集中的噪声从0增加到20%时,VT-SVDD方法的分类精度变化最小,对噪声的干扰表现最为稳健;其次是K-NN和PSVDD;传统SVDD和SVMs对噪声较为敏感。总之,本文提出的VT-SVDD方法不仅改进了传统SVDD方法的稳健性,与其他常用分类方法相比也是比较稳健的。
在传统SVDD方法中,作为定值的惩罚因子决定了数据描述的精度,然而实践中惩罚因子的选择是极其困难的,为了解决这一矛盾,本文提出了一种可变惩罚因子的稳健支持向量数据描述方法(VT-SVDD)。这种方法基于样本点在核空间的位置分布,为每个样本点计算一个惩罚因子,然后基于这种可变惩罚因子求解一个凸约束二次规划,就可以得到对数据集的球形域描述。在UCI数据集上进行了无噪声、有噪声两个方面的仿真实验,结果表明,VT-SVDD方法提升了传统SVDD方法的精确度和稳健性。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|


