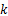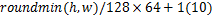申铉京(1958),男,教授,博士生导师.研究方向:图像处理与模式识别,多媒体信息安全,智能控制技术.E-mail:xjshen@jlu.edu.cn
为了提高拼接篡改图像的检测准确率,利用视觉注意模型提出了一种新的图像拼接篡改盲鉴别算法。首先,采用改进的基于OSF的非线性滤波方法提取图像的边缘信息,得到边缘显著图像ECM;其次,利用视觉注意模型提取ECM的注意点,并采用显著边缘定位法锁定图像显著边缘处注意点,进而获取图像关键特征片段;接着,提取图像片段的Cr通道,并计算其小波重构图像;然后,针对小波重构图像,提取其扩展的DCT域的HMM特征,并采用SVM-RFE算法对所提取特征进行降维处理;最后,根据得到的特征向量,利用SVM对特征值进行训练并建立分类模型,从而实现自然图像和拼接篡改图像的分类识别。实验结果表明,针对哥伦比亚大学拼接篡改图像库,本文算法的正确检测率为96.32%。
In order to improve the detection accuracy of spliced images, a new blind detection based on the Visual Attention Model (VAM) was proposed in this study. First, the Edge Conspicuous Map (ECM) is created by an improved Order Statistics Filter (OSF) based nonlinear filtering approach; then, the ECM fixations are extracted by VAM, and the fixations on the boundaries are located by conspicuous edge positioning method, accordingly the key feature fragments are captured. Second, the Extended Hidden Markov Model (E-HMM) features are extracted from each wavelet reconstructed image of Cr channel of the fragments, and their dimensions are reduced by SVM-RFE. Finally, the above features are trained and classified using SVM, by which the spliced images can be identified from the natural ones. The experimental results show that, when testing on the Columbia image splicing detection dataset, the detection accuracy of the proposed method is 96.32%.
数字图像盲鉴别技术,旨在不依赖任何预签名提取或预嵌入信息的前提下,对图像的真伪和来源进行鉴别[ 1],它是一种新的图像鉴别分析思路[ 2]。图像拼接是最常见的篡改手段之一,将两幅或多幅图像拼接成一幅伪造图像,通常会造成图像场景信息、统计数据等的改变。Qu等[ 3]提出一种基于人类视觉系统和多层分类模型的图像拼接检测算法,该算法在哥伦比亚大学拼接篡改图像库[ 4]的检测率为94.07%,但是该算法具有较高的计算复杂度,并且需要利用边缘模板提供边缘信息。Lin等[ 5]提出一种可以快速、自动定位篡改区域的检测算法,然而该算法的平均检测率为60%,并且检测图像仅限于JPEG图像。Zheng等[ 6]提出局部尖锐、模糊等级度量法用于拼接图像检测,但是该算法的检测率仅达到62%。Dong等[ 7]提出一种将基于游程和边缘信息特征函数高阶矩作为特征向量的图像拼接篡改检测方法,但是该算法检测率也仅为76.52%。He等[ 8]提出基于近似游程的图像拼接篡改检测算法,该改进算法的检测率略有提高,为80.58%,但依然没有显著提高。
为了提高对拼接篡改检测的准确率,本文基于视觉注意模型(Visual attention model,VAM)[ 9],构造扩展的DCT域隐马尔可夫特征(Extended-hidden Markov model,E-HMM)向量,利用SVM分类器进行拼接篡改图像的盲鉴别。实验结果表明,本文算法的检测率达到了96.32%。
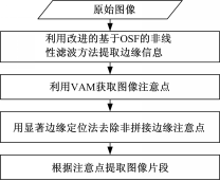
本文提出一种基于视觉注意模型VAM和扩展的隐马尔可夫特征E-HMM的拼接篡改图像盲鉴别算法,其基本流程如图1所示:
(1)通过训练图像构造用于建立分类模型的特征向量。首先,采用改进的基于OSF的非线性滤波方法得到边缘显著图像(Edge conspicuous map,ECM)。然后,针对ECM利用视觉注意模型提取其注意点,采用显著边缘定位法锁定图像显著边缘处注意点,并据此获取图像的关键特征片段。接着,提取图像片段的Cr通道,并计算其小波重构图像。最后,针对关键特征片段的小波重构图像,提取其扩展的DCT域的HMM特征,并采用SVM-RFE算法对所提取特征进行特征筛选构造本文算法特征向量。
(2)利用以上提取的特征向量,用SVM训练并建立分类模型。
(3)对于检测图像,以同样的方法提取、构造特征向量,并利用得到的分类模型进行检测。
为了使提取的图像特征对拼接篡改更加敏感,首先获取图像的关键特征片段,然后再提取这些片段的特征。基于此,本文提出一种利用视觉注意模型(VAM)提取图像关键特征片段的方法。算法流程如图2所示:
图像拼接篡改会在拼接边缘引入一些不易察觉的边、角、块信息,这些信息比自然图像更加尖锐。因此,提取图像显著边缘信息对拼接篡改的检测至关重要。基于次序统计滤波器(Order statistic filter,OSF)的非线性滤波方法[ 3]会抑制那些波动相对缓慢区域的边缘的灰度峰值。图3(a)所示为拼接篡改图像,图3(b)为对图3(a)进行OSF滤波得到的均衡尖锐图像(Normalized sharpness map,NSM)。
自然图像中无灰度波动的区域,如白炽灯,经过抑制会与其周围形成巨大反差而成为图像可疑区域,如图3(c)(图3(c)为图3(b)的局部放大)所示:
另外,自然图像中,如铁栅栏、窗框等笔直边缘,也会造成VAM对注意点的误判,如图3(d)(图3(d)为图3(b)的局部放大)所示。因此,本文提出了改进的基于OSF的非线性滤波方法。设滤波器为 
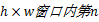
Step1 对图像每个通道 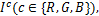
水平方向滤波得到降噪图像 
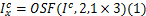
水平方向求一阶导数得到 

计算水平方向一阶导数与滤波图像差值的绝对值 
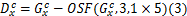
Step2 结合三通道计算水平方向均衡边缘。
累加 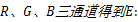
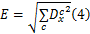
计算水平方向均衡边缘 

式中: 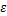
用同样的方法可得到垂直方向均衡边缘 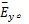
Step3 计算加强的均衡边缘图像。
水平、垂直方向均衡边缘的最大值 
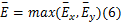
加强的均衡边缘图 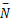
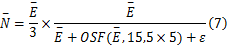
Step4 提取最终边缘显著图像ECM。
加强均衡边缘图的梯度值 

边缘显著图ECM为
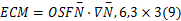
通过式(7)计算加强的均衡边缘图,使图像边缘比均衡边缘图更加突出。另外,由于梯度指向标量场增长最快的方向,而梯度值是这个方向的最大变化率,因此,对于加强的均衡边缘图,式(9)利用梯度值对其进行处理,不仅可以减少梯度值较小的笔直边缘,也可以抑制大部分均匀波动区域,从而降低无灰度波动区域与其周围区域形成的反差。并且,对其进行次序统计滤波,对图像做平滑处理,使得图像边缘信息更加清晰,图3(e)所示为对图3(a)提取的ECM(为了便于观察,对ECM进行了二值化处理)。
在提取的边缘显著图像ECM中,拼接边缘比自然图像的边缘更加尖锐,因此可以利用视觉注意模型(VAM)提取这些边缘的注意点,进而获取图像关键特征片段。
将ECM作为输入,利用MATLAB中VAM的工具箱Saliency Toolbox[ 9],生成特征显著图(Saliency map,SM)。搜索SM中具有局部最大值的点,这些点就是特征注意点,图4(a)所示:
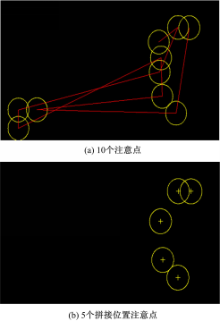 | 图4 VAM锁定ECM的10个注意点及5个拼接位置注意点Fig.4 10 located fixations of ECM by VAM and 5 fixations located on splicing edges |
为利用VAM提取的10个特征注意点。实验发现,针对拼接篡改图像利用上述过程搜索到的注意点并非全部在拼接边缘处,如图4(a)中左边3个点不在拼接边缘。与非拼接边缘处的注意点相比,拼接边缘的注意点具有以下特点:①具有较强的空间聚类性;②区域内灰度值较大;③区域内仅有一条边缘。基于此,为了提高片段提取以及拼接检测的准确率,本文提出显著边缘定位法锁定 
Step1
对于提取的10个特征注意点(当注意点个数超过10,注意点在拼接边缘的概率极低)计算两两注意点之间的欧式距离。
Step2
将距离值最小和次小的两个注意点对分别记入集合 
Step3
由于拼接边缘区域的灰度值较大,因此计算以注意点为中心、大小为13×13的矩形灰度和 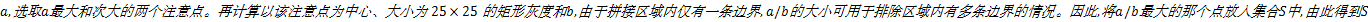
Step4
搜索与 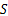
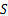
Step5
返回Step4,直到 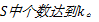
DCT域隐马尔可夫特征对拼接图像检测有良好的效果[ 10],但是其忽略了块间相关性,而图像拼接篡改往往会破坏这种块间相关性。因此,本文综合考虑HMM特征及其块间相关性,提取图像关键特征片段的扩展HMM特征,并构造特征向量。
首先,由于图像的YCbCr比RGB三通道对图像拼接更为敏感[ 11],因此对于获取的图像关键特征片段,提取其Cr通道。
然后,计算其离散小波重构图像。对输入图像 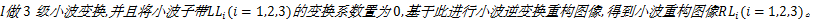
最后,针对小波重构图像,提取扩展的DCT域隐马尔可夫特征(E-HMM)。
用传统方法得到的隐马尔可夫特征是所有转移概率矩阵的元素,其构成了 
Step1 对图像进行8×8块DCT变换,得到DCT变换系数。
Step2 对DCT变换系数取整,并取绝对值,得到矩阵 
Step3 分别计算水平、垂直、主对角线和次对角线的8×8块间差分矩阵,依次为 


式中: 
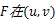
Step4 引入阈值 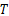
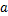

Step5 计算水平、垂直、主对角线和次对角线的转移概率矩阵,依次为 
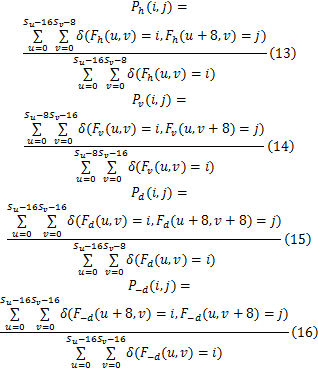
式中: 
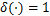
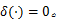
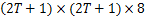
图像拼接检测是一个典型的二分类模式识别问题,然而无法确切得到恰好能将待检测图像正确分类的某一个特征。因此,需要从获得的一系列特征中选取最利于图像检测分类的特征。
对于包含 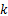
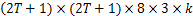
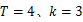
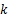
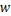
利用SVM-RFE将E-HMM特征向量排序,生成特性排序表,选取前 
本文算法的实验平台为AMD Athlon 7750 Dual-Core CPU 2.70 GHz,2 GB内存,Microsoft Visual Studio 2008,编程语言为C++。
选择LIBSVM[ 13]作为分类器,其中核函数为径向基函数(RBF)。使用Grid-Search方法[ 14]寻找最优的参数对 
本文采用两种方法来评价算法性能:一种是ROC曲线(Receiver operating characteristics curve)的AUC(Area under ROC),AUC越大,分类效果越好;另一种是自然图像正确检测率(TP)和篡改图像正确检测率(TN)以及综合检测率(Accuracy)。
(1)Y、Cb、Cr通道选择
在构造E-HMM特征向量时,首先要提取关键特征片段的Y、Cb、Cr通道,并计算其离散小波重构图像。Y、Cb、Cr通道对本文算法性能具有不同的影响,通过对数据库进行测试,其统计结果如表1所示: 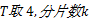
| 表1 Y、Cb、Cr三通道对本文算法的影响 Table 1 Experiment results of the proposed approach of Y,Cb and Cr channels |
其中阈值由表1数据可知,在Cb、Cr通道求取特征值有较好的检测效果,因此实验中提取片段Cr通道的特征。
(2)阈值 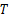
阈值 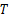
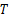
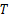

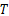
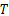
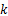
| 表2 不同参数 T对本文算法的影响 Table 2 Experiment results of the proposed approach with different threshold T |
其中选取Cr通道,分片数由表2数据可知,当 T=4时,本文算法的检测率最高。但是,对比 T=2或者 T=3的检测率并没有显著提高。因此,若在大规模批量检测中,计算代价需更受重视, T=2或者 T=3会更加适合。出于对实验阶段高准确率的要求,本文选取 T=4。
(3)图像关键特征片段数 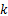
图像的片段数量由VAM提取的显著边缘注意点的个数决定,个数越多,建立分类模型时可选择的特征向量就越多,建模越精确,但是相应的计算代价也会加大。对于拼接图像,选取注意点过多,会出现注意点不在拼接位置的情况。因此,选取Cr通道,阈值 T取4来验证不同分片数对本文算法的影响,统计结果如表3所示:
| 表3 不同分片数 k对本文算法的影响 Table 3 Experiment results of the proposed approach with different fragment k |
由表3数据可知,当 k=3时,并没有充分获取图像中拼接篡改信息,使得建立的分类模型不够精确;当 k=5时,所选信息增多,但是其中包含部分未被拼接篡改的图像片段,这往往由于图像内容细节信息(如窗框等)对算法的误导,进而造成建模误差。当 k=4时,算法检测率达到了96.32%。
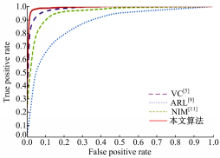
文献[3]利用视觉注意模型搜索图像的前 k个注意点,并以注意点信息构造多层分类模型底层的特征向量。文献[8]基于近似游程直方图特征函数的高阶矩构造特征向量,是目前十分前沿的检测方法。文献[10]在拼接篡改图像检测中具有非常高的检测率。所以,为了对比分析本文算法的性能优势,在相同的实验平台下基于相同的实验数据库(哥伦比亚大学拼接篡改图像库),作者将本文算法与这3个算法进行对比分析。
图6为本文算法与其他3种算法的ROC曲线,通过AUC可见,本文算法具有最好的分类效果。
文献[3]采用多层分类器,对特征维度的比较没有意义,所以针对TP、TN和Accuracy三个性能参数,对该算法与本文算法进行分析,统计结果如表4所示:
| 表4 本文算法与文献[3]算法的比较 Table 4 Comparison between the proposed approach and the method in reference [3] |
由表4中数据可知,本文算法的TP、TN和Accuracy均优于文献[3]的算法,主要是因为文献[3]存在以下3个方面的不足:①未考虑不在拼接位置注意点的情况,只是简单提取前 k个注意点,因此,窗框、栅栏等笔直边缘会造成建模误差;②需要利用边缘模板提取注意点;③利用多层分类器,加大了提取图像特征的计算复杂度。
表5为本文算法与文献[8]和文献[10]就检测率和特征维度进行对比分析的统计结果。
| 表5 本文算法与文献[8]和文献[10]算法的比较 Table 5 Comparison between the proposed approach and the methods in reference [8] and [10] |
由表5数据可知,本文算法优于文献[8]和文献[10]的检测效果,并且在特征维度上也有较好的平衡。其原因主要有两个:①本文算法对图像采取分片手段以集中图像中最敏感部分的信息,并通过SVM-RFE进行特征筛选,选取最优的特征向量来降低特征维度,因此与文献[8]的全局纹理特征相比,本文算法的特征信息更具有针对性;②与文献[10]采用的HMM特征相比,本文采用的E-HMM特征提供了更多敏感的统计特征,使本文算法的检测率得到了提高。
基于改进的非线性滤波方法得到的边缘显著图ECM,利用视觉注意模型以及显著边缘定位法获取图像的关键特征片段,并针对关键特征片段Cr通道的小波重构图像提取其扩展的DCT域的HMM特征,并采用SVM-RFE算法对其进行降维处理。与现阶段相对前沿的算法相比,本文算法大大提高了图像检测率。但是,对于拼接区域经过模糊、图像修复等后处理的拼接图像,本文算法在检测率上还有较大的改进空间,作者将在以后的工作中继续研究鲁棒性更强的算法。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|