赵晓晖(1957),男,教授,博士生导师.研究方向:信号处理理论在通信中的应用.
对于多中继OFDM放大转发协作通信系统,在各个中继节点功率独立受限的条件下,中继节点转发子载波的数目较多时,每个子载波所能分配到的功率较少,而将此中继节点转发的部分子载波转由空闲的中继节点转发,可以获得更大的功率增益。为此,本文提出了一种改进算法。在中继节点距离源节点较近时,充分利用空闲中继节点的功率,提高系统容量,在中继节点距离源节点较远时,削减中继节点数目,降低系统复杂度。仿真结果表明,本文算法在中继节点距离源节点较近时获得了更大的系统容量,在中继节点距离源节点较远时,保持系统容量基本不变,降低系统复杂度,易于实现。
For multi-relay-assisted Orthogonal Frequency Division Multiplexing (OFDM) cooperative systems with Amplify-and-Forward (AF) mode, when relay nodes are close to the source node, higher system gain can be achieved, otherwise, the system will get lower gain. Under the condition that each relay node has individual power constraint, the more subcarriers relay nodes forward, the less power of each sub-carrier is allocated. Greater power gain can be acquired when some of the sub-carriers are forwarded by idle relay nodes instead of the previous busy node. Therefore, we propose an improved algorithm. In this algorithm, when relay nodes are close to the source node, we make full use of the power of the free relay nodes to increase system capacity. When relay nodes are far from the source node, the relay node number is reduced to decrease system complexity. Simulation results show that the improved algorithm can obtain higher system capacity when the relay nodes are close to the source node, and it also can approximately maintain system capacity unchanged with lower system complexity when relay nodes are far from the source node.
在未来移动通信系统中,多输入多输出(MIMO)技术是在无线衰落环境中实现高数据传输速率和提高系统容量的重要途径之一[ 1]。在无线频谱资源缺乏和非常昂贵的情况下,MIMO系统的优势已经得到了业界广泛的认同,然而受到节点尺寸以及发射功率的限制,使MIMO技术的实现变得复杂和困难。协作通信技术因其可以充分利用无线电波的广播特性,使无线网络中的节点可通过相互协作形成虚拟的天线阵列获得传统MIMO技术的空间分集增益[ 2]。因此,协作通信作为一种新型的通信模式受到人们越来越多的关注。在协作通信系统中,中继节点的选取以及功率分配一直是协作通信系统研究的热点[ 3, 4, 5],两者之间相互影响,决定了协作能否带来系统通信性能的提高。本文研究了多中继OFDM协作通信系统的中继节点选择和功率分配算法。由于中继系统采用OFDM调制技术,所以还涉及到子载波配对问题[ 6],因此,需要给出子载波配对算法。目前,已经有这方面的研究成果出现。在文献[7]中,Duval等人提出了一种选择性子载波中继和功率分配方案,这种算法与传统OFDM系统的算法相比提高了系统的吞吐量,但是只适用于单中继OFDM系统。文献[8-9]在多中继OFDM协作通信系统中,将中继节点选择以及子载波和功率的分配联合进行优化,这种联合优化算法可以取得很好的性能,但是计算复杂度很大。为了简化计算,通常将中继选择、子载波配对和功率分配三者分别进行独立优化,文献[10]将分步优化的方法应用到了多中继OFDM系统中,提高了系统的吞吐量。但文献[10]仅根据信道条件来选择中继节点,而不考虑中继节点的位置及转发子载波的数目对系统性能的影响。
本文针对文献[10]存在的这一问题,提出了一种改进算法。当中继节点距离源节点近时,子载波通过中继节点转发获得的增益较大,令没有转发子载波的中继节点选择一个对其信道增益最高的子载波进行转发,使这个子载波获得此中继节点的全部功率。当中继节点距离目的节点较远时,子载波通过中继节点转发获得的增益会逐渐降低,令中继系统中只转发一个或两个子载波的中继节点不参加转发,减少参与转发的中继节点数,降低了系统的复杂度。
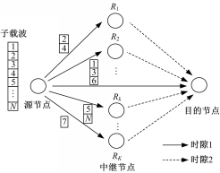
多中继OFDM系统模型如图1所示:
源节点通过K个中继节点与目的节点进行通信,OFDM系统中有N个子载波,采用放大转发模式,源节点和中继节点采用半双工方式。将一帧分成两个等长的时隙,在第一个时隙,源节点以广播的方式将子载波传送到目的节点和K个中继节点;在第二个时隙,中继节点根据子载波分配矩阵 A,将接收的数据转发给目的节点。子载波分配矩阵 A定义为 A k.i =
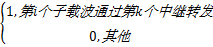 | (2) |
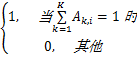
假设信道衰落系数在每个传输时隙是不变的,考虑到无线信道路径衰落损耗特性,假定第l径衰落信道的信道衰落系数服从复高斯分布:hl~CN 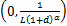
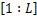
(3)式中:d为源节点与目的节点之间的距离;L为信道抽头系数;α为路径损耗因子。
对式(3)进行N点FFT变换,即可得到信道增益的频域响应。Hsd,i表示子载波i在源节点和目的节点间传输时的信道增益, 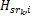
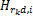
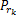
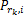
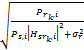
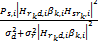
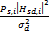
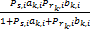
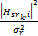
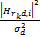
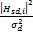
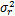
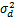
如果子载波i通过中继节点转发到目的节点,则此子载波上获得瞬时信道容量可以表示为CR,i= 
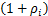
直接传输的子载波,瞬时信道容量为CS,i= 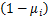
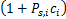

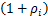
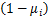
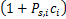
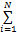
当多中继OFDM系统中所有的子载波都通过中继转发时,称为所有子载波中继。系统容量的表达式为C= 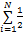
(1)中继选择
由于每个子载波只能通过一个中继进行转发,因此对于每个子载波都选择对其本身信道增益最优的中继进行转发。采用文献[10]中定义的ak,i和bk,i的调和平均数作为参考标准,定义为Wk,i= 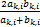
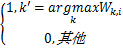
在中继选择方案确定之后,对给定的子载波分配矩阵进行最优的功率分配。
中继节点功率优化:假定源节点功率均等分配,每个中继节点都有独立的功率约束,为了简化,令 K个中继节点提供的功率相等,即 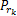
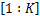
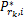
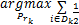
s.t 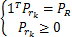
在 P s均等分配的情况下,通过使用 KKT条件求解[ 11]使目标系统容量最大时的 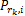
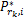
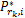
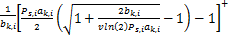
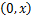
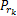
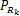
源节点功率优化:在给定中继功率优化方案的情况下,源节点功率优化的目标函数如下: 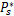
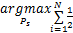
s.t 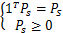
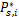
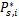
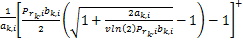
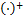
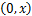
对式(14)(16)进行迭代运算,直到结果收敛。
根据子载波转发是否能带来增益而进行选择性转发,称为选择性子载波中继。文献[10]给出每个子载波所承载容量的表达式如下: C i = 

log2 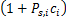
式(17)的第一部分表示子载波 i通过第 k个中继转发所获得的容量增益。定义容量增长因子为 Ξ 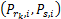

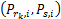
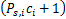
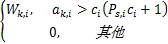

子载波 i通过第 k个中继转发能带来增益所需的最小功率为 γ k, i = 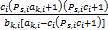
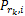
(2)子载波配对
对于两跳链路的中继网络,信道的传输特性在第一跳和第二跳中可能会相差很大,这样就会限制系统的容量。因此,在两种中继选择方案确定后要对两跳链路子载波配对来提高系统的性能。
(3)功率分配
在中继选择方案和子载波分配矩阵确定后,在源节点和各中继节点功率分别约束的条件下,对源节点和中继节点进行最优的功率分配。
中继节点功率分配:假定源节点功率均等分配,为了简化,令 K个中继节点提供的功率相等,即 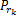
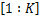
优化问题可以表示如下: 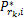
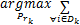
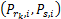
s.t 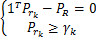
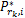
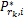
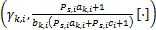
式中:
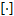
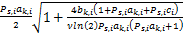
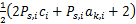
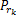
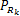
源节点功率分配:在中继节点子载波功率分配方案 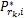
对于参与转发的中继节点, a k, i >c i始终满足。条件 Ξ 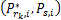
Γ k, i = 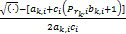
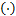

4 a k, i 
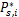
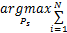
s.t 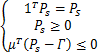
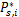
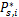
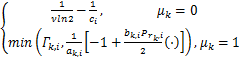
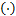
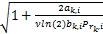
当子载波通过中继节点进行转发时,源节点和目的节点之间的信道增益为 H sd, i≪1,这样式(5)的第二部分可以忽略不计。将上述两个优化步骤迭代执行,直到结果收敛为止。
现有算法[ 10]仅根据信道条件来选择中继节点,并没有考虑中继节点的位置及转发子载波的数目对系统性能的影响。在中继节点距离源节点较近时,中继节点的转发可以获得较大的增益。但存在部分中继节点转发多个子载波,而部分中继节点没有转发子载波的现象。由于中继节点功率独立受限,使得转发较多子载波的中继节点的功率分配给多个子载波,每个子载波所能分配到的功率较少。而空闲的中继节点没有被有效利用,为了使中继节点充分利用,令没有转发子载波的中继节点选择一个对其信道增益最高的子载波进行转发,这样这个子载波就可以分配到此中继节点的全部功率,使系统容量获得增益。
改进的算法具体如下:
(1)寻找中继节点 k *,满足 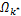
(2)对于已求解的 k *,求解子载波 i∈ Ψ k 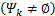
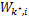
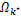
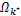
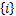
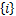
(3)重复步骤(1)(2),直到 S=∅。
(4)进行子载波配对和功率分配,计算系统容量 C。
改进算法中 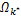
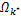
当中继节点逐渐向目的节点靠近时,子载波通过中继节点转发获得的增益会降低。当上述算法获得的系统容量值不高于文献[10]中算法获得的系统容量时,令中继系统中只转发一个或两个子载波的中继节点不参加转发,这样可以在保持系统容量基本不变的情况下,降低系统复杂度,提高功率效率。具体算法如下:
(1)寻找只转发一个或两个子载波的中继节点 k。
(2)对于中继节点 k转发的子载波 i,寻找除中继节点 k之外,调和系数 W k, i最大的中继节点 k '。
(3)将子载波 i改为由中继节点 k'转发,更新调和系数矩阵 W '和子载波分配矩阵 A '。
(4)返回步骤(1),直到每个参与转发的中继节点至少转发3个子载波。
(5)进行子载波配对和功率分配,计算系统容量 C。
本文的仿真结果是通过10 000次蒙特卡洛仿真实验得到的。在仿真实验中,源节点的功率值 P s满足源节点和目的节点之间的平均信噪比为ρk =0 dB,假设源节点与中继节点的功率相同, 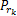
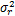
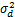
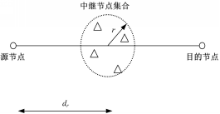
中继节点分布如图2所示:
数量为 K=8,随机分布在半径r =100 m的圆形区域里,此圆形区域的圆心与源节点的距离为 d r,而且同源节点和目的节点在一条直线上。源节点与目的节点的距离为d =1000 m。 OFDM系统中子载波数为 N=32。
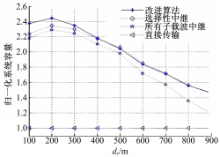
图3给出了不同分配方案的归一化系统容量。从图中可以看出,在 d r=200 m时,各种方案都达到系统容量的最大值,在 d r>200 m时,随着dr的增大,系统容量呈下降趋势。dr取任意值时,选择性中继系统容量都要高于所有子载波中继时容量。在 d r<400 m时,改进算法可以获得更高的系统容量,而在 d r≥400 m时,选择性中继与改进算法比较接近。
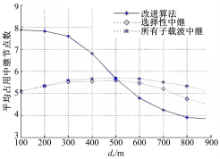
图4给出了不同方案占用中继数的平均值。选择性中继算法与所有子载波中继算法在 d r<300 m时占用的中继数基本相同, d r≥300 m时,选择性中继占用的中继数小于所有子载波中继算法。改进算法占用的中继数随着dr的增大而降低,在 d r<500 m时占用的中继数多于其他两种算法,这是由于空闲的中继节点参与了转发过程,在 d r≥500 m时,由于削减了中继节点的个数,占用的中继数低于其他两种算法。
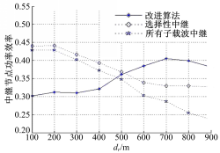
图5给出了不同方案的中继节点功率效率。中继节点功率效率定义为归一化系统容量与中继个数的比值。从图中可以看出,选择性中继的功率效率始终高于所有子载波中继算法。改进算法在 d r<500 m时功率效率低于其他两种算法,在 d r≥500 m时,功率效率高于其他两种算法。
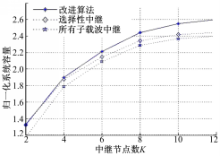
图6给出了归一化系统容量随中继节点数K的变化情况,仿真条件设定为 d r=200 m,N=32。从图中可以看出,算法的归一化系统容量随中继节点个数的增加而增加,获得了分集增益。在中继节点K=2和K=4时,改进算法与选择性转发的系统容量接近,这是由于中继节点个数少时,改进算法对其子载波分配影响较小。反之,随着中继节点个数的增多,改进算法的容量开始明显增加。
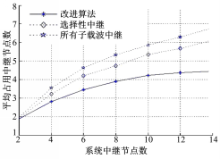
图7给出了平均占用的中继节点数随系统总的中继节点数的变换情况,仿真条件设定为 d r=800 m,N=32。从图中可以看出,随着系统中继节点个数的增多,选择性中继与所有子载波中继两种算法占用的中继节点数增加,而改进算法占用的中继节点数趋于平稳。说明在中继节点远离源节点时,本文提出的改进算法可以使系统保持较低的复杂度。
在考虑中继节点的位置及转发子载波的数目对系统性能影响的基础上,提出了一种改进的资源分配算法。仿真结果表明,在中继节点与源节点距离较近时,改进算法可以使没有转发子载波的中继节点功率得到利用,从而提高系统容量。在中继节点距离源节点较远时,改进算法将只转发少量子载波的中继节点转为空闲状态,将其转发的子载波转由其他中继节点转发,不仅能保持系统容量基本不变,而且可以降低系统复杂度,提高功率效率,使系统易于实现。在实际应用中,应该根据用户的服务质量要求和中继节点的位置分布来合理选择资源分配方案,本文提出的改进算法在此方面提供了新的思路。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|