陈建(1977),男,讲师,博士.研究方向:阵列信号处理,无线通信及应用.E-mail:chenjian@jlu.edu.cn
提出了两种基于稀疏重构的高分辨波达方向(DOA)估计方法。对空间进行粗、细两步网格划分,并在相应的过完备基下获得阵列协方差矩阵列向量的稀疏表示,分别基于剔除及差分处理抑制噪声干扰影响。采用lp范数约束正则化迭代加权最小范数(FOCUSS)算法进行稀疏重构,在重构过程中,对过完备基进行奇异值分解并剔除奇异值小于阈值项以减小计算量,并解决过完备基条件数过大带来的病态问题。仿真结果验证了所提算法的有效性和鲁棒性。
This paper presents two methods of high-resolution direction-of-arrival estimation based on signal sparse representation. First, a coarse-refined grid separation is created, which is used to structure the sparse representation of array covariance column vectors corresponding to overcomplete basis. Then, a removing and differencing method is employed to suppress the inference of noise. A regularized FOCUSS algorithm with lp norm constraint is applied for sparse reconstruction. Finally, the Singular Value Decomposition (SVD) is adopted to remove the singular value, which is less than the threshold to reduce complexity as well as ill-posed problem of overcomplete basis. Simulation results validate the effectiveness and robustness of the proposed method.
传统的Capon、MUSIC和ESPRIT[
针对上述问题,本文提出了两种新的稀疏DOA估计方法,首先利用阵列协方差矩阵各列向量的稀疏表示构建稀疏矩阵,然后分别基于剔除及差分处理抑制噪声干扰,通过奇异值分解及阈值处理克服网格细划分下过完备基条件数过大带来的病态问题。最后,通过仿真试验验证了所提算法的有效性。
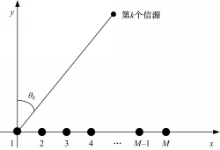
假设有K个远场窄带信号从不同的入射方向θk(k=1,2,…,K)入射到M(>K)元均匀线阵上,阵元间距为d,如图1所示:
以第一个阵元为相位参考点,高斯白噪声背景下t时刻阵列输出可表示为
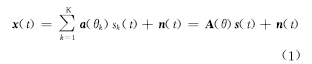
式中: s( t) =[ s1( t), s2( t),…, s K( t)]T为零均值信号向量; n( t)为零均值、方差为 σ2的噪声向量; A( θ)为 M×K的阵列流型矩阵,其第 k列(代表第 k个信号)的导向矢量为
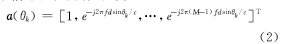
式中: f为载波频率; c为传播速度。
为了将传统的 DOA估计问题转变为稀疏信号重构问题,假定空间存在 N( >M)个可能的波达方向,则式(1)可重新表示为

式中: s '( t)为 K稀疏的信号向量,其非零元素对应于 s( t); B( θ)为过完备基,具有典型的 Vandermonde矩阵结构,表示为

针对式(3)表示的数据矩阵,利用文献[5 -8]中的稀疏重构算法求解式(3)的欠定方程组即可得到 DOA估计,然而由于噪声的存在,算法稳健性难以保障。为此采用二阶统计量获得阵列输出的协方差矩阵
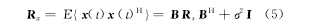
式中: R s =E{ s '( t) s 'H( t)} =diag{ P1, P2,…, P N}为 K稀疏的信号协方差矩阵; P i为假定的第 i个信号的功率; I为 M×N的单位矩阵。
取 R x的第 m( m=1,2,…, M)列,表示为 
(1)剔除处理
以牺牲一定的阵列孔径为代价,在式(6)的基础上剔除 R x的第 m个元素,表示为 R xr= B r R ' s(7)式中: R xr为 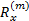
(2)差分处理
对式(3)进行如下变化得 y( t) = Jx( t)(8)式中: J为 M阶反向单位矩阵,假设采用关于 y轴对称的网格划分形式,则 y( t)可表示为 y( t) = JB( θ) s'( t) + Jn( t) =
B( θ) DJ N s '( t) + Jn( t)(9)式中: J N为 N阶反单位矩阵; D为 N×N的对角矩阵,其第 p( p=1,2,…, N)个对角元素表示为 d p = 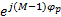

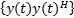
BDJ N R s J N DH BH(11) 对 R y和 R x进行差分得 R d= R y- R x= JR x J - R x=
B( DJ N R s J N DH - R s) BH(12) 当信源不相关时,式(12)可简化为 R d= B( J N R s J N- R s) BH(13)取 R d的第 m列,表示为 
本文基于式(7)(14)进行稀疏重构,可有效地抑制噪声干扰的影响,同时,由于只需进行单次重构,在一定程度上降低了计算量。
在阵列协方差矩阵各列向量稀疏表示及剔除与差分处理的基础上,对空间进行粗(如0.5°~1°)、细(如0.01°~0.1°)两步网格划分,在每次网格划分后对相应的过完备基进行SVD分解:
B = UΛVH = U
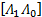 | (15) |
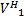
式中: Λ1为M个大奇异值组成的矩阵; 
在网格划分中,尤其是网格细划分中,过完备基 B条件数较大,最小范数解是严重病态的,将明显降低算法估计性能。为此,本文采用阈值化处理并设定阈值为 q,在 SVD分解后采用剔除奇异值小于阈值 q的处理,在一定程度上减小过完备基条件数的同时,还可进一步降低算法的运算量。其中阈值 q经验上一般取0 .1 ~1,受限于阵元数、系统对信噪比的要求等,一般情况下,阵元数越多,阈值 q的取值宜越小,相反地,信噪比越低,阈值 q的取值宜越大。
为了获得不确定线性系统模型 Φx = b的稀疏解,文献[4]从谱估计的角度给出了基本的 FOCUSS迭代算法: x( a)= W a 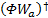
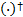
无噪声干扰时,基本的 FO CUSS算法可以获得较好的局部最优解,然而由于 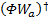
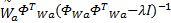
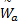
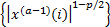
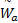
折中考虑稀疏性与优化问题的凸性,当0 .8≤p≤1时,算法可以得到较精确的解。
以下仿真实验中,考虑由9个阵元组成的 ULA阵列,阵元间距为0 .5倍波长,在加性高斯白噪声背景下,采用 l p范数约束正则化 FOCUSS方法进行稀疏重构,实验中正则化参数 λ=0 .1, p=0 .8。为了方便起见,分别取 R xr、 R d的第一列作为观测值,基于式(7)和式(14)的稀疏重构算法定义为 VFOCUSS和 DFOCUSS,基于式(7)和式(14)过完备基进行奇异值分解及通过阈值处理后再进行稀疏重构的方法分别定义为 SVDVFOCUSS和 SVDDFOCUSS。均方根误差定义为RMSE = 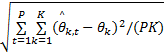
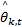
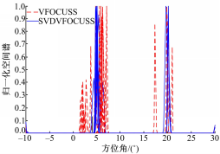
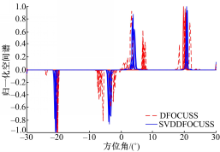
实验1 考虑两个窄带非相关信源 DOA估计情况,入射角度分别为θ1 =5 °,θ2 =20 °, SNR=5 dB,快拍数为500,以0 .1 °进行空间网格划分,阈值p设定为0 .1。10次独立 Monte-Carlo实验结果如图2和图3所示:
为了便于说明,实验中采用归一化空间谱输出结果。特别地,图3中的负峰值为伪峰,由差分操作引入,可通过正负符号判断去除。可以看出,本文所提的两种方法均可以有效地抑制过完备基条件数过大带来的病态问题。
实验2 考虑两个邻近窄带非相关信源DOA估计情况,入射角度分别为 θ1=15°, θ2=20°,快拍数为200。图4为SNR=10 dB和SNR=0 dB条件下SVDVFOCUSS、SVDDFOCUSS方法与经典CAPON方法、MUSIC方法的空间谱输出对比。SNR=10 dB时,除CAPON方法外均能很好地分辨两个信源,当SNR降低至0 dB时,本文所提的两种方法仍能很好地分辨两个信源,而MUSIC方法模糊了两个峰值,显示了本文所提算法具有较高的分辨率性能。
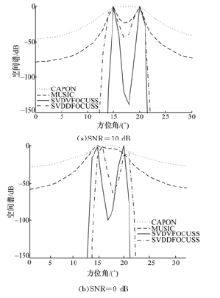 | 图4 SVDVFOCUSS、SVDDFOCUSS与CAPON、MUSIC的空间谱对比Fig.4 Spatial spectrum of SVDVFOCUSS、SVDD-FOCUSS、CAPON、MUSIC |
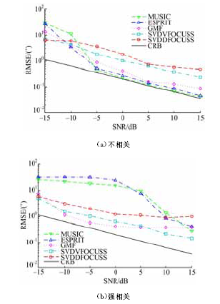
实验3 分别考虑两个窄带不相关和相关(相关系数0.99)信源DOA估计情况,入射角度分别为 θ1=10°, θ2=20°,快拍数为200,设定阈值为 p=0.1,信噪比由-15 dB变化到15 dB,每种信噪比做100次Monte-Carlo实验。由图5(a)可以看出,当信源不相关时,本文方法估计性能在低信噪比条件下最好,而在中、高信噪比条件下性能低于其他方法,这是由于FOCUSS类方法本身并不是全局最优导致的。同时还可以看到,SVDVFOCUSS方法在相同条件下优于SVDDFOCUSS方法,这是由于差分运算会带来一定的孔径损失。在信源强相关或相干条件下,如图5(b)所示,本文方法在中、低信噪比条件下具有优于MUSIC和ESPRIT的估计性能。特别地,在低和高信噪比条件下,SVDVFOCUSS方法具有最好的估计性能,而在中信噪比条件下接近GMF方法。值得指出的是,虽然GMF方法在某些条件下优于本文所提的两种方法,其计算量也明显高于本文方法,参见文献[9],因此本文所提算法可以认为是在计算量与估计精度间的一个很好的折中。
提出了两种新的基于二阶统计量与FOCUSS相结合的稀疏DOA估计方法,该方法通过剔除及差分处理降低噪声干扰,通过取列向量和对过完备基进行奇异值分解并经合理的阈值化处理可降低算法复杂度及抑制过完备基条件数过大带来的病态问题,与经典子空间方法相比,本文方法不仅具有更高的分辨率,而且具有对相关信源的强稳健性。与GMF方法相比,本文方法可认为是在计算量与估计精度间的一个很好的折中。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|