引用本文
司伟建, 吴迪, 陈涛. 基于部分重合信号的空间谱估计新方法. 2014, 44(2): 490-496[SI Wei-jian, WU Di, CHEN Tao. New spatial spectrum estimation method based on partly overlapped signals. 吉林大学学报(工学版), 2014, 44(2): 490-496]  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于部分重合信号的空间谱估计新方法
司伟建, 吴迪, 陈涛
哈尔滨工程大学 信息与通信工程学院,哈尔滨 150001

司伟建(1971),男,研究员.研究方向:宽带信号的检测、处理和识别.E-mail:swj0418@263.net

基金:国家自然科学基金项目(61201410/F010301); 中央高校基本科研业务费重点专项项目(HEUCFZ1215);
摘要

为了提高色噪声背景下空间谱估计多重信号分类(MUSIC)算法的分辨率,根据诱饵信号覆盖雷达信号时,实际被动测向系统接收脉冲信号部分重合的特点,提出了一种色噪声背景下空间谱估计的新方法。首先对接收数据进行分段,然后估计每段数据的信源数,最后对各段接收数据的协方差矩阵对角线进行归一化,利用协方差差值MUSIC算法,给出各信号的协方差矩阵,通过多次谱峰搜索,分步得到信号波达方向(DOA)估计结果。计算机仿真及实际系统测试均验证了所提出的方法是可行的。

关键词: 通信技术; DOA估计; 色噪声; 差值MUSIC算法; 部分重合; 分辨率
中图分类号:TN911 文献标志码:A 文章编号:1671-5497(2014)2-490-7
New spatial spectrum estimation method based on partly overlapped signals
SI Wei-jian, WU Di, CHEN Tao
College of Information and Communication Engineering, Harbin Engineering University,Harbin 150001,China
Fund:
Abstract

In order to improve the resolution of spatial spectrum estimation multiple signal classification (MUSIC) algorithm in the presence of colored noise fields, a new spatial spectrum estimation method was proposed. This method is based on the receiving characteristic of pulse signals in an actual direction finding system, when decoy signals overlap radar signals. In this method, first, the receiving data are divided into several segments; then the number of signals of every receiving data segment is estimated; finally, the covariance matrix of every receiving data segment is normalized by covariance matrix diagonal elements. The covariance matrix of every signal is given by using covariance difference MUSIC algorithm. By searching spectrum peak, the result of Direction of Arrival (DOA) estimation can be obtained step by step. Both simulation and test based on actual direction finding system prove the proposed method realizable.

Keyword: communication; DOA estimation; colored noise; difference MUSIC algorithm; part overlap; resolution
0 引 言

反辐射导弹被动测向系统通过处理接收的雷达辐射源信号估计雷达信号波达方向[ 1],从而进行精确打击。随着雷达技术的发展,现代雷达系统通常采用在目标雷达周围配置诱饵的方式保护雷达。各个诱饵辐射的脉冲信号间存在一定的延时,通常诱饵发出的脉冲至少超前其所保护雷达0.1~0.2 μs[ 2, 3],使诱饵辐射的脉冲信号合成的覆盖脉冲可以遮盖住雷达天线旁瓣产生的脉冲,对于这种诱饵信号覆盖雷达信号的情况,目前反辐射导弹所广泛使用的基于相位干涉仪的被动测向方法只能实现对单个信号的测向。空间谱估计方法可以对一个波束宽度内多个入射信号的来波方向进行估计,同时具有测角精度高、角度分辨力强等优点,因而备受关注。其中以Schmidt提出的MUSIC算法[ 4]最为突出。然而,MUSIC测向算法是在高斯白噪声背景下提出的,在实际系统中由于阵元各通道幅度和相位的不一致、通道内部噪声不一致等因素的影响,天线阵元接收的噪声往往是色噪声。因此色噪声背景下多信号的波达方向估计是比较重要的问题[ 5, 6, 7]。针对此问题,文献[8]利用迭代循环算法改善了非均匀噪声环境,但是迭代循环使算法变得复杂。文献[9]提出了一种基于噪声子空间解析形式的快速DOA估计算法,计算量小于传统的超分辨DOA估计,但是算法仅对于特殊阵列形式适用。文献[10]利用协方差矩阵前向、后向平滑消除了色噪声的干扰,但是需要采用两个分置且相互垂直的均匀线阵。文献[11]通过迭代的形式,利用交替加权最小二乘法对噪声功率进行估计,从而通过预白化的方法去除色噪声对DOA的影响,但是需要有稳健的DOA估计初值。文献[12]通过利用估计的噪声相关矩阵进行预处理,消除空间非平稳噪声对算法的影响,但该方法只可应用于线阵。文献[13]在文献[12]的基础上将算法的应用范围扩展到了圆阵,但是该算法需要在阵元数大于三倍的信源数时适用。

本文针对有诱饵信号覆盖雷达信号时诱饵信号与雷达信号构成部分重合信号的特点,在色噪声背景下提出了一种空间谱估计的新方法。该方法对数据协方差矩阵对角线元素进行归一化处理,有效去除色噪声影响,并与协方差差值MUSIC算法相结合,构成协方差归一化差值MUSIC算法,实现使用5阵元均匀圆阵对三个辐射信号的正确分辨,得到二维DOA估计结果。

1 新方法的提出

假设系统中存在一个雷达信号和两个诱饵信号,图1给出了诱饵信号与雷达信号的脉冲时序关系。

图1 雷达信号与诱饵信号时序关系示意图Fig.1 Radar and decoy signal time sequence diagram

诱饵信号与雷达信号的合成信号构成部分重合信号,各部分由不同的信号合成。目前反辐射导弹大多通过接收信号的前沿或后沿取样来跟踪雷达。这时简单的空间谱估计方法的估计性能将会变差或无法准确跟踪雷达。从而,需要针对部分重合信号的特点,提出空间谱估计的新方法。

首先,采集不完全重合部分的数据,根据信号的幅度信息对采样数据进行分段。以两个同频信号为例,到达接收天线时,两个信号可分别表示为S1(t)=a1(t) exp[j(ωt+φ1)](1)

S2(t)=a2(t) exp[j(ωt+φ2)](2)于是,天线阵列的其中一个阵元所接收的信号可表示为S(t)=S1(t)+S2(t)=

a1(t) exp[j(ωt+φ1)]+a2(t) exp[j(ωt+φ2)](3)式中:a1(t)和a2(t)分别为两个信号的幅度;φ1和φ2为两信号到达天线1时刻的初相。

令U1表示一个辐射信号时接收天线接收到的信号幅度;U2表示两个信号叠加时接收天线接收到的合成信号幅度;A1、A2分别表示两个信号的瞬时幅度最大值;φ1、φ2分别表示三信号到达一个接收天线时的初相。则U1=A1(或者A2)(4)

U2=[ + +2A1A2 cos(φ1-φ2)]1/2

(5) 由式(4)(5)可以看出,接收信号由不同信号组成时,信号的幅度不同。所以当诱饵信号覆盖雷达信号,合成信号构成部分重合信号时,信号幅度就会发生跳变,以此可作为信号分段的依据。

其次,估计每段数据的信号源个数。将部分重合信号分段后,每段数据由不同个数的信号组成。由于色噪声的存在,此时AIC和MDL准则等基于信息论准则的信源数估计方法会出现过估计。通过对接收数据矢量的协方差矩阵对角线元素进行归一化处理,使其包含的色噪声变成各阵元之间功率相等的白噪声,此时利用常规的信源数估计方法,可得每段数据包含的准确的信源个数。

最后,使用本文提出的协方差归一化差值MUSIC算法,分步估计每个入射信号的来波方向。

2 算法原理
2.1 信号模型

设空间有M个天线阵元组成的均匀圆阵阵列,有N个远场窄带辐射信号,其中第i个(i=1,2,…,N)信号的入射角度信息为(θi,φi),入射信号间相互独立,噪声为色噪声,各阵元之间的噪声相互独立,并且噪声与信号之间也相互独立。则阵列的输出写成矢量形式为 X( t) = A( θ, φ) S( t) + N( t)(6)式中: X( t)为 M×1维的接收数据矢量; A( θ, φ) =[ a( θ1, φ1), a( θ2, φ2),…, a( θ N, φ N)]为空间阵列的 M×N维的导向矢量阵, a( θ i, φ i)为第 i个( i=1,2,…, N)信号的导向矢量,且 a( θ i, φ i) =

(7)

ψ ki = [cos( -θ i)cos φ i](8) N( t) = 为空间阵列的 M×1维噪声矢量; S( t) =[ s1( t), s2( t),…, s N( t)]T为空间信号的 N×1维矢量;阵列输出的数据协方差矩阵为 R X =E[ X( t) XH( t)] = AR S AH + Q N(9)式中: R S =E[ S( t) SH( t)]为信号协方差矩阵; Q N =E[ N( t) NH( t)]为噪声的协方差矩阵,假定各阵元之间的噪声相互独立,功率不相等,则噪声协方差矩阵满足 Q N =diag( , ,…, ),其中 ( i=1,2,…, M)表示噪声功率。

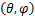
对协方差矩阵进行特征分解,将其特征值按降序排列为 λ1≥ λ2≥…≥ λ M,它们所对应的特征向量为 v1, v2,…, v M,且各特征向量是相互正交的,则 R X的噪声子空间 U N为 U N = (10)构造空间谱函数 PMUSIC = (11)连续改变θ、φ值,进行谱峰搜索,由此得到N个最大值所对应的θ、φ值就是N个信号源的角度。

2.2 协方差归一化差值MUSIC算法

对于图1所示的情况,设雷达信号为S1(t),两诱饵信号分别为S2(t)和S3(t),对合成信号进行前沿采样(一定包含不完全重合部分),根据采样数据的幅度信息,可将数据分为3段,用信源数估计方法估计每段数据的信源数。可知,第一段数据包含1个辐射信号,第二段数据包含2个辐射信号,第三段数据包含3个辐射信号,对包含信号源个数最多的数据段(第三段),基于经典MUSIC算法的原理,阵列接收数据可表示为 X( t) = A( θ, φ) S( t) + N( t) =

[ a( θ1, φ1) a( θ2, φ2) a( θ3, φ3)]·

[ S1( t) S2( t) S3( t)]T + N( t)(12)协方差矩阵 R X =E[ X( t) XH( t)] =

A( θ, φ) E[ S( t) SH( t)] AH( θ, φ) + Q123 =

[ a( θ1, φ1) a( θ2, φ2) a( θ3, φ3)]·

E + Q123 =

a( θ1, φ1) R1 aH( θ1, φ1) + a( θ2, φ2) R2 aH( θ2, φ2) +

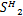
a( θ3, φ3) R3 aH( θ3, φ3) + Q123(13)式中: R1 =E[ S1( t) ( t)]为第一个入射信号的相关矩阵; R2 =E[ S2( t) ( t)]、 R3 =E[ S3( t) ( t)]分别为第二个和第三个入射信号的相关矩阵; Q123为3个信号同时入射时接收数据的噪声功率。

对于第一段数据,只有一个信号 S1( t),阵列接收数据协方差矩阵可表示为 =E[ X1( t) ( t)] =

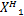
A( θ) E[ S1( t) ( t)] AH( θ) + Q1 =

a( θ1) R1 aH( θ1) + Q1(14)式中: Q1为一个信号入射时阵列接收数据的噪声功率。

对于第二段数据,由 S1( t)与 S2( t)的合成信号构成,阵列接收数据协方差矩阵可表示为 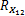= a( θ1) R1 aH( θ1) + a( θ2) R2 aH( θ2) + Q12(15)式中: Q12为两个信号入射时阵列接收数据的噪声功率。

观察式(13)(14)(15)可以发现,多个信号同时入射时阵列接收数据的协方差矩阵等于各信号单独入射时阵列接收数据协方差矩阵的和。利用协方差矩阵的这个特点,当可以先得到其中一个或两个信号的协方差矩阵,又得到多个信号同时入射的协方差矩阵时,将多个信号的协方差矩阵与其中部分信号的协方差矩阵相减,即可以得到其余信号的协方差矩阵。

将式(13)与式(15)相减,可得 R X - = a( θ3) R3 aH( θ3) + Q1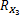23 - Q12 =

a( θ3) R3 aH( θ3) + Q3 = (16)式中: Q3为两协方差矩阵相减后的噪声功率。

基本的 MUSIC算法中假定噪声为白噪声,即对于式(9)中, Q N =σ2 I M, I M为单位阵,同时信号协方差矩阵 R S =E[ S( t) SH( t)] =

diag (17)式中: p i为第 i个阵元接收信号的功率。

假设各天线阵元通道增益相同,则阵列输出的数据协方差矩阵对角线元素值近似相等。但是由于色噪声的影响,使得数据协方差矩阵对角线元素值差距较大,从而严重影响 MUSIC等空间谱估计算法的性能。这时对接收数据矢量的协方差矩阵对角线元素进行归一化,将此方法称为协方差归一化方法。将协方差归一化算法与协方差差值算法相结合,构成协方差归一化差值算法,算法实现过程如下。

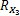
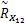
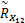
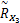
由协方差差值算法可知: = R X - (18) 设归一化变换矩阵为 ,令 为式(18)中协方差矩阵 的对角线元素,即 =diag[ (1,1) (2,2)… ( M, M) ](19) 对协方差矩阵对角线元素进行归一化变换,得到新协方差矩阵 ,则协方差归一化差值 MUSIC算法得到的协方差矩阵 = 。设 =diag[ (1,1) (2,2)… ( M, M) ](20) 对协方差矩阵对角线元素进行归一化变换,得到新的协方差矩阵 ,则 = 。

对 做特征分解,进行一次谱峰搜索,得到信号 S1( t)与 S2( t)的入射角度;对 做特征分解,再进行一次谱峰搜索,得到信号 S3( t)的入射角度。从而得到了每个信号的 DOA估计。

将上述方法推广到多个辐射信号入射的情况,当有 N个辐射信号入射时,阵列接收数据的协方差矩阵可以写为 R X =E[ X( t) XH( t)] =

a( θ1, φ1) R1 aH( θ1, φ1) + a( θ2, φ2) R2 aH( θ2, φ2) +

… + a( θ N, φ N) R N aH( θ N, φ N) + Q N =

+ +… + + Q N(21)式中: ( N=1,2,…, N)为各信号单独入射时的协方差矩阵。

如果已知其中 N-1个辐射信号的协方差矩阵,很容易就可以得到第 N个辐射信号的协方差矩阵。当其他条件一定时,入射信号个数越多,算法正确分辨多信号的概率越低。而协方差归一化差值 MUSIC算法将对同时入射的多个信号的 DOA估计问题转化为对少数信号或者单个信号进行分步 DOA估计的问题,虽增加了运算时间,但是大大提高了空间谱估计对多信号的分辨性能。当然算法成立的前提是入射信号构成部分重合信号。

本文方法的实现步骤如下:

(1)对部分重合信号采样,得到采样数据,根据采样数据幅度信息,对数据进行分段。

(2)估计每段数据的信源个数。

(3)根据接收数据得到协方差矩阵 和 R X,并根据式(18)得到差值协方差 。

(4)对协方差矩阵 、 进行对角线元素归一化处理,得到新的协方差矩阵 、 。

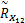
(5)分别对协方差矩阵 、 进行特征值分解,确定信号子空间和噪声子空间。

(6)由式(11)构造空间谱,通过两次谱峰搜索,得到三个信号的 DOA估计结果。

后端的抽取参数值用来达到对动态变化的子带信号近似完全重建的目的。

3 实验分析

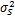
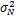
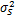
信噪比定义为SNR =10lg( / )(22)式中: 为第一个阵元接收噪声的功率; 为信号的功率。

分辨概率定义为正确估计信号 DOA的次数与实验次数的比值。

3 .1 仿真实验分析

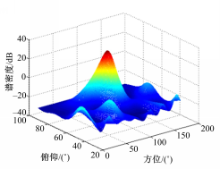
仿真条件:采用半径为124 mm的5元均匀圆阵,快拍数取100。噪声协方差矩阵取 R N = diag[1,0 .4,3 .2, 10,2 .6]。由于仿真实验中空间谱值较大,对式(11)进行取对数处理,得到空间谱图。

实验1 两个频率为3 GHz的信号入射到天线阵列,入射角度分别为(80 °,75 °)和(110 °,65 °),信噪比为0 dB。 MUSIC算法、协方差差值 MUSIC算法与本文提出的协方差归一化差值 MUSIC算法的空间谱图分别如图2、图3和图4所示:

图2 MUSIC算法的DOA估计Fig.2 DOA estimation by MUSIC algorithm

图3 协方差差值MUSIC算法的DOA估计Fig.3 DOA estimation by covariance difference MUSIC algorithm

图4 本文所提算法的DOA估计Fig.4 DOA estimation by the proposed algorithm

由图2可知,色噪声背景下传统的MUSIC算法不能分辨两个入射信号。由图3(a)可知,协方差差值MUSIC算法对一个信号入射时的DOA估计结果为(82.5°,75.5°);图3(b)为协方差差值MUSIC算法对两个信号重合时的协方差,与其中一个信号的协方差相减之后的差值协方差进行估计的谱峰图,DOA估计结果为(105.5°,66.5°)。可见,协方差差值MUSIC算法可以正确估计两个入射信号,但是估计精度不高。由图4(a)可知,本文提出的算法对一个信号的DOA估计结果为(79.5°,75°);图4(b)为本文提出算法对两个信号重合时的协方差与其中一个信号的协方差相减之后的差值协方差进行估计的谱峰图,DOA估计结果为(110°,62.5°)。仿真结果证实了本文提出算法的有效性。

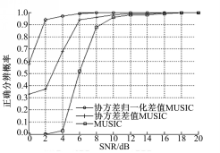
实验2 频率为6 GHz,角度间隔相差5°的两个信号入射到天线阵列,利用MUSIC算法、协方差差值MUSIC算法和本文提出的协方差归一化差值MUSIC算法进行100次Monte Carlo实验,统计不同信噪比下3种算法的角分辨概率,如图5所示:

图5 不同信噪比下的角分辨概率Fig.5 Angle resolution probability of different SNR

从图5可以看出,随着信噪比的增大,算法的角分辨概率提高。比较3种算法的角分辨概率可知,在仿真条件一致时,本文提出的协方差归一化差值MUSIC算法的分辨性能较好。

3.2 实测数据分析

实测条件:实验环境为18 m×10 m×5.5 m的微波暗室,天线阵列为半径124 mm的5元均匀圆阵,3个频率为6 GHz的独立辐射源信号,入射角度分别为(86°,0.5°)、(85°,172°)和(78°,48.5°),按照图1给出的脉冲时序关系设置三信号,对接收数据进行前沿采样,快拍数取100,利用本文给出的DOA估计方法进行仿真实验。

图6 MUSIC算法的DOA估计Fig.6 DOA estimation by MUSIC algorithm

图6为MUSIC算法直接对3个脉冲信号重合部分(第三段数据得到)进行估计的谱峰图,可见,存在一个图中标出坐标的伪峰,无法得到正确的DOA估计结果。图7(a)为本文提出算法估计两个信号入射时(第二段数据得到)的谱峰图,DOA估计结果为(86°,-1.5°)、(85°,174.5°);图7(b)为本文提出算法对三个脉冲信号重合时(第三段数据得到)的协方差与其中两个信号的协方差(第二段数据得到)相减之后的差值协方差进行估计的谱峰图,DOA估计结果为(79°,46°)。

实际系统的测试结果验证了本文提出方法在实际测向系统中的可实现性及有效性。

图7 本文算法的DOA估计Fig.7 DOA estimation by the proposed algorithm

4 结束语

根据实际系统工作时接收的脉冲信号部分重合的特点,提出了一种色噪声背景下信号空间谱估计新方法。首先对数据进行分段,然后估计每段数据信源数,最后使用本文提出的协方差归一化差值MUSIC算法,分步估计入射信号的来波方向。经过仿真及实际测向系统测试,证明此方法在相同条件下具有更高的DOA估计角分辨率。虽然多次谱峰搜索耗时较长,但是可以估计更多的辐射信号个数,将本文方法与快速算法相结合,同时采用高速的DSP器件并行处理等方法,使算法得到实现。

The authors have declared that no competing interests exist.

参考文献
[1] Gao F F, Nallanathan A, Wang Y D. Improved MUSIC under the coexistence of both circular and non circular sources[J]. IEEE Trans on Signal Processing, 2008, 56(7): 3033-3038. [本文引用:1]
[2] 韩英臣, 张永顺, 冯存前, 等. 雷达抗ARM诱饵系统时序设计与仿真[J]. 航天电子对抗, 2002(3): 12-14.
Han Ying-chen, Zhang Yong-shun, Feng Cun-qian, et al. Simulation and design of radar dec-oy time sequence for counterating anti-radiati-on Missile[J]. Aerospace Electronic Warfare, 2002(3): 12-14. [本文引用:1] [CJCR: 0.2072]
[3] 段晓超. 诱饵时序控制的实现[J]. 现代电子, 2002(1): 26-28.
Duan Xiao-chao. An implementation of deeoy time sequence control[J]. Modern Electronics, 2002(1): 26-28. [本文引用:1] [CJCR: 0.5199]
[4] Schmidt R O. Multiple emitter location and signal parameter estimation[J]. IEEE Trans on Antennas and Propagation, 1986, 34(3): 276-280. [本文引用:1] [JCR: 2.332]
[5] Hansen P C, Jensen S H. Prewhitening for rank-deficient noise in subspace methods for noise reduction[J]. IEEE Trans on Signal Processing, 2005, 53(1): 3718-3726. [本文引用:1]
[6] 吴云韬, 廖桂生, 陈建锋. 一种色噪声环境下的DOA估计新方法[J]. 电子学报, 2001, 29(12): 1605-1607.
Wu Yun-tao, Liao Gui-sheng, Chen Jian-feng. A novel method for estimating DOA in the presence of unknown colored noise fields[J]. Acta Electronica Sinica, 2001, 29(12): 1605-1607. [本文引用:1] [CJCR: 0.686]
[7] 周欣, 石要武, 郭宏志. 有色噪声背景下多径信号的二维DOA和极化参数同时估计算法[J]. 吉林大学学报: 工学版, 2009, 39(3): 797-802.
Zhou Xin, Shi Yao-wu, Guo Hong-zhi. Algorithm for estimating 2-D direction of arrival and polarization of multiple signals in colored noise[J]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39(3): 797-802. [本文引用:1] [CJCR: 0.701]
[8] Chiao En Chen, Lorenzelli F, Hudson R E, et al. Stochastic maximum-likelihood DOA estimation in the presence of unknown nonuniform noise[J]. IEEE Trans on Signal Processing, 2008, 56(7): 3038-3044. [本文引用:1]
[9] 艾名舜, 马红光, 刘刚. 基于噪声子空间解析形式的快速DOA估计算法[J]. 电子与信息学报, 2010, 32(5): 1071-1076.
Ai Ming-shun, Mang Hong-guang, Liu Gang. DOA estimation algorithm base on analytical solution of noise subspace[J]. Journal of Electronics & Information Technology, 2010, 32(5): 1071-1076. [本文引用:1] [CJCR: 0.087]
[10] 刘兆霆, 阮谢永, 刘中. 色噪声背景下基于声矢量阵列孔径扩展的相干目标波达方向估计[J]. 兵工学报, 2011, 32(3): 257-263.
Liu Zhao-ting, Ruan Xie-yong, Liu Zhong. Coherent target direction-of-arrival estimation based on aperture expansion of acoustic vector array under colored noise[J]. Acta Armamentarii, 2011, 32(3): 257-263. [本文引用:1] [CJCR: 0.5149]
[11] 刘成城, 赵拥军, 杨静. 色噪声背景下的幅相误差自校正算法[J]. 电子信息对抗技术, 2011, 26(4): 9-13.
Liu Cheng-cheng, Zhao Yong-jun, Yang Jing. Array gain and phase self-calibration algorithm in the presence of colored noise[J]. Electronic Information Warfare Technology, 2011, 26(4): 9-13. [本文引用:1]
[12] Wu Yun-tao, Hou Chao-huan, Liao Gui-sheng, et al. Direction-of-arrival estimation in the presence of unknown nonunform noise fields[J]. IEEE on Oceanic Engineering, 2006, 31(2): 504-510. [本文引用:1]
[13] 曾耀平, 齐云. 空间非平稳噪声下圆阵的DOA估计[J]. 电子科技, 2008, 21(2): 76-78.
Zeng Yao-ping, Qi Yun. DOA estimation bas-ed on circular array in the presence of spati-allly nonstationary noise fields[J]. Electronic Science & Technology, 2008, 21(2): 76-78. [本文引用:1] [CJCR: 0.3174]