引用本文
王戈, 沈智翔, 于宏毅. 基于期望最大化算法的联合符号检测和相位估计算法. 2014, 44(2): 497-501[WANG Ge, SHEN Zhi-xiang, YU Hong-yi. Joint symbol detection and phase estimation algorithm based on expectation-maximum. 吉林大学学报(工学版), 2014, 44(2): 497-501]  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于期望最大化算法的联合符号检测和相位估计算法
王戈1,2, 沈智翔1, 于宏毅1
1.中国人民解放军信息工程大学 信息工程学院,郑州 450002
2.中国西安卫星测控中心,西安 710043

王戈(1982),男,博士研究生.研究方向:通信信号处理,信号解调算法.E-mail:superwangge@sohu.com

基金:国家重大科技专项项目(2008ZX03006); “863”国家高技术研究发展计划项目(2012AA121606);
摘要

针对带有未知载波相位的符号检测问题,提出了一种基于期望最大化(EM)算法的联合符号检测与相位估计算法,该算法改变了传统最佳接收算法中先估计载波相位再进行符号检测的分级处理方式,直接通过EM算法进行符号检测。在算法收敛之后,判决获得符号信息的同时,可得到未知载波相位的最大似然(ML)估计,从而实现了符号信息与载波相位的联合估计与检测。由于该算法不需要进行同步参数估计,因此可以大大降低传统最佳接收方法分级处理方式所带来的性能损失。仿真实验表明,该算法与传统最佳接收算法中先通过非数据辅助(NDA)方法估计载波相位再进行符号检测相比,性能有明显提升,可以达到导频辅助下的符号检测性能,由于不需要估计载波相位,因此处理复杂度大大降低。

关键词: 通信技术; 期望最大化算法; 符号检测; 相位估计; 误符号率
中图分类号:TN911.23 文献标志码:A 文章编号:1671-5497(2014)2-497-5
Joint symbol detection and phase estimation algorithm based on expectation-maximum
WANG Ge1,2, SHEN Zhi-xiang1, YU Hong-yi1
1.InstituteInformationEngineering,ThePLAInformationEngineeringUniversity,Zhengzhou 450002,China
2.ChinaXi'anSatelliteControlCenter,Xi'an 710043,China
Fund:
Abstract

In this paper, the problem of symbol detection in the presence of unknown carrier phase is studied. A joint symbol detection and phase estimation algorithm based on the Expectation-Maximum (EM) algorithm is developed, which is different from the traditional optimum receive algorithm. The algorithm does not need to estimate the carrier phase and obtain symbol information directly. After the algorithm convergence, it obtains signal information, at the same time estimates the maximum-likelihood (ML) of unknown carrier phase, and consequently realizes the joint symbol detection and phase estimation. Because the algorithm does not require synchronization parameters estimation, it can reduce the loss of performance, which is brought by the hierarchical processing of the traditional method. Simulation results show that, in comparison with the traditional optimum receive algorithm, which has to estimate the phase by non-data-aided first, then detect symbol information, the performance of the proposed algorithm is improved significantly.

Keyword: communication; expectation-maximization algorithm; symbol detection; phase estimation; symbol error rate(SER)
0 引 言

突发通信中,接收机所接收到的每个突发数据包都带有不同的未知载波相位。对于未知载波相位的符号检测问题,传统最佳接收方法是先估计载波相位,再进行符号检测的分级处理,因此不能很好地适用于突发通信中。同时由于非数据辅助的载波相位估计性能不佳,因此对数据检测的误码性能也有很大影响[ 1, 2]。期望最大化(Expectation-maximization,EM)算法[ 3]是一种求解参数最大似然估计的迭代算法,在处理“不完全数据”中有重要应用。基于EM算法的同步参数估计的理论框架以及基于EM算法的符号定时,载波频率偏移和载波相位相偏估计等在文献[4-5]中已有介绍。文献[6-7]给出了一种基于EM算法的联合序列检测和相位估计算法,该算法直接通过前一次的符号判决值计算载波相位,因此是一种将符号与相位按照判决反馈原理进行迭代求解的算法,没有对未知载波相位进行平均,因此不能算是一种基于EM的符号检测算法。文献[8]是在通过EM算法对符号取平均估计载波相位的同时获得符号软信息,将迭代中的符号后验概率最大值作为符号硬判决结果,该算法也是在基于NDA载波相位估计算法的基础上完成的,因此误码性能仍然受到影响。文献[9-10]给出了OFDM系统中使用EM算法进行联合信道估计和符号检测的算法。

本文针对带有未知载波相位偏移的符号检测问题,提出了一种基于EM算法的符号检测算法。该算法与传统最佳接收算法相比不需要估计载波相位,直接通过EM算法进行符号检测,在获得符号信息的同时,根据最大后验概率(MAP)准则可以得到载波相位偏移的最大似然(ML)估计,从而实现了符号与载波相位的联合检测与估计,其性能与传统非数据辅助(NDA)载波相位估计算法之后再进行符号检测的分级处理方式相比有明显提升。

1 信号模型

假设在定时信息完全已知的条件下,接收信号模型为

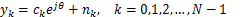(1)

式中:yk为匹配滤波器输出的采样信号;ck为发送符号;θ为未知的载波相位;nk为均值为0、方差为σ2的复加性高斯白噪声。

接收信号序列yk关于符号ck和未知载波相位θ的联合条件概率密度为p(yk|ck,θ)=

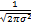(2)
exp

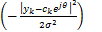
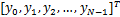
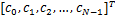
令 y = 为接收的信号矢量; c = 为发送符号矢量。写为矢量形式为

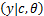
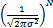
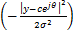
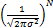p = exp =

(3)
exp

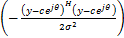
可得对数似然函数为

ln p =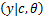

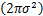
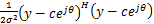
- ln - =

-

（4）
ln -

2 算法描述
2.1 基于EM的符号检测算法

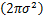
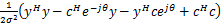
令 c为待估计参数,取 θ为隐变量,则构成完备数据 x =[ y, θ]。通过 EM算法迭代求解似然函数ln p 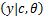的最大值。

(1) E( Expectation)步

Q函数可写为

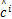
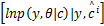
Q( c, )=E θ =

E θ =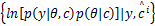

E θ +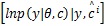

E θ

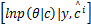（5）

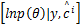
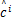
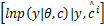
式(5)中第二项符号信息 c与相位信息 θ无关,可写为 E θ ,该式也与待估计参数无关,不会影响EM算法中M步的最大值求解问题,可以忽略,因此式(5)可写为Q( c, )=E θ =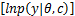

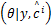
∫ θ p d θ （6）

由 Bayes公式和全概率公式可得:

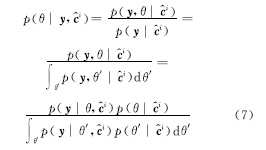
由于载波相位θ与符号信息 c无关,假设 θ在[0, π/2]服从均匀分布,可得:

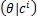
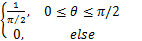p =p(θ)=

(8)

p

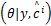(9)
=

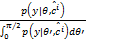
所以,将式(9)代入到式(6)可得:

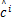
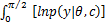
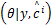
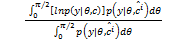Q( c, )= p d θ=

(10)

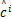
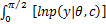
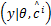
在式(10)中,去掉与 c无关的项,对M步中的最大值求解无影响,因此可得:Q( c, )= p d θ (11)

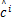
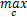
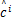
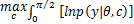
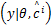
(2) M( Maximum)步 =arg Q( c, )=

arg p d θ(12)

即利用 p 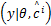和对数似然函数ln p( y |θ, c)迭代求解。

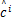
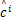
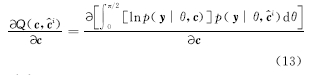
在 Q( c, )中,对数似然函数只有单个极值,并且函数关于极值点对称,可利用距离极值点最近的离散值来替代该极值点,因此可以将符号 c看作连续变量对 Q( c, )求偏导,可得:

式中:

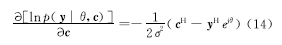
将式(14)代入到式(13),并令偏导数为0,有:

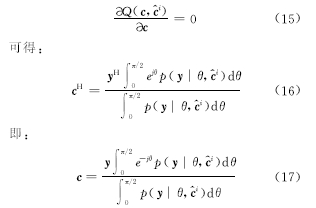
将式(3)代入式(17)可得: c =

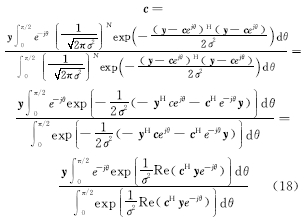
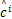
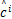从式(18)可得, c为符号的软信息,因此根据最小欧式距离准则,判决符号 为

(19)
=arg

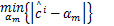
式中:α m为用于符号判决的标准星座点集合。

综上所述,基于 EM的符号检测算法步骤如下:

Step1 设定迭代次数 i=0,选取符号初值 c0=0。

Step2 根据式(18)计算 c i+1。

Step3 i=i+1,重复 Step2,直至算法收敛( c i+1= c i)。

2.2 载波相位估计

2.1节中给出了基于EM算法的符号检测算法,在第i次迭代中载波相位估计值为

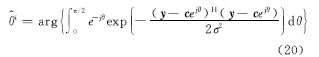
随着算法的收敛,在得到符号信息的同时也得到了载波相位的估计值,实现了符号与载波相位的联合检测与估计。

2.3 载波相位在积分区间边缘时的改进算法

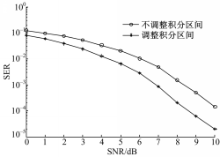
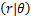
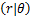
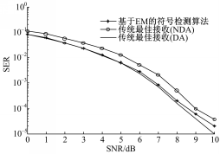
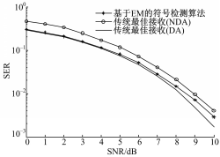
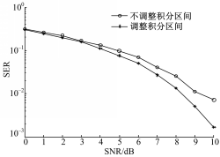
在式(18)给出的符号检测中,当载波相位偏移位于积分区间边缘时,即p 的峰值位于积分区间的边缘,会导致符号检测性能恶化。因此,可以通过调整积分区间的方法进行改进,即当检测得到符号信息的同时联合估计出的载波相位值位于积分区间边缘时,调整积分区间使得p 的峰值位于积分区间中间,从而改善符号检测性能。

3 性能仿真
3.1 误符号率

针对2.1节描述的符号检测算法,对BPSK和QPSK的误符号率性能进行统计,与传统最佳接收算法进行比较。

本文所用的传统的最佳接收算法,首先通过V&V算法估计未知的载波相位,然后对接收信号进行相位偏移补偿,最后根据最小欧式距离准则判决接收。从图1和图2可以看出,基于EM算法的符号检测算法误码性

图1 BPSK误符号率性能Fig.1 The SER of BPSK

图2 QPSK误符号率性能Fig.2 The SER of QPSK

能较传统最佳接收算法中先通过非数据辅助(NDA)方法估计载波相位再进行符号检测相比,性能有明显提升,可以达到导频辅助下的符号检测性能。

3.2 载波相位估计性能

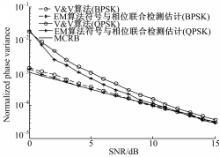
考虑未编码的MPSK信号( M=2,4),初始相偏为θ= π/6,符号长度为1000,对相位估计标准差与估计均值进行仿真分析。

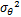
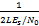
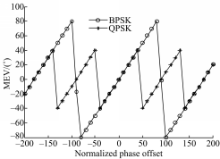
MPSK信号载波相位估计的MCRB为[ 11, 12] = (21)式中:L为数据长度;E s/N0为符号信噪比。

图3给出了联合符号检测与相位估计算法和基于V&V算法的载波相位估计算法的估计方差曲线,从图3可以看出,本文所提出的算法性能明显优于V&V算法。图4给出了本文所提出算法的载波相位估计均值曲线,从图4中可以看出,该算法在估计范围内均线性良好。

图3 相位估计标准方差Fig.3 Standard deviation of phase offset estimation

图4 相位估计均值Fig.4 Mean of phase offset estimation

3.3 载波相位在积分区间边缘时改进后算法的性能

针对2.3节描述的改进符号检测算法,对BPSK和QPSK的误符号率性能进行统计。对载波相位在积分区间边缘时调整积分区间与不调整积分区间符号检测性能进行比较。图5和图6分别给出了载波相位偏移θ=4 π/9时BPSK算法和θ=2 π/9时QPSK算法改进前后的误符号率性能曲线。

图5 BPSK误符号率性能Fig.5 The SER of BPSK

图6 QPSK误符号率性能Fig.6 The SER of QPSK

4 结束语

针对未知载波相位的符号检测问题,提出了一种基于EM算法的联合符号检测和相位估计算法。该算法改变了传统接收算法中先估计载波相位再进行符号检测的分级处理方式,直接通过EM算法进行符号检测。在获得了符号信息的同时,可以得到载波相位的ML估计,从而实现了符号与载波相位的联合检测与估计,性能较传统基于NDA载波相位估计算法之后再进行符号检测有明显提升,可很好地应用于突发通信中。

The authors have declared that no competing interests exist.

参考文献
[1] Moeneclaey M, Jonghe G. ML-oriented NDA carrier synchronization for general rotationally symmetric signal constellations[J]. IEEE Transactions on Communications, 1994, 42(8): 2531-2533. [本文引用:1] [JCR: 1.75]
[2] Gworghiades Costas N. Blind carrier phase acquisition for QAM communication[J]. IEEE Transactions on Communications, 1997, 45(11): 1477-1486. [本文引用:1] [JCR: 1.75]
[3] McLachlan G J, Krishnan T. The EM Algorithm and Extensions[M]. New York: Wiley Series in Probabil Statist, 1997. [本文引用:1]
[4] Noels N, Herzet C, Dejonghe A, et al. Turbo synchronization: an EM algorithm interpretation[C]∥IEEE International Conference on Communication, 2003. [本文引用:1]
[5] Assra A, Hamouda W, Youssef A. EM-based joint channel estimation and data detection for MIMO-CDMA systems[J]. IEEE Transactions on Vehicular Technology, 2010, 59(3): 1205-1216. [本文引用:1] [JCR: 2.063]
[6] Dempster A P, Laird N M, Rubin D B. Maximum-likelihood from incomplete data via the EM algorithm[J]. J Roy Stat Soc, Ser B, 1977, 39(1): 1-38. [本文引用:1]
[7] Zamiri-Jafarian Hossein, Pasupathy Subbrayan. Adaptive MLSDE using the EM algorithm[J]. IEEE Transactions on Communications, 1997, 47(8): 1181-1193. [本文引用:1] [JCR: 1.75]
[8] Nassar'Carl R, Soleymani M Reza. Joint sequence detection and phase estimation using the EM algorithm[C]∥Conference on Electrical and Computer Engineering, Canada, 1994. [本文引用:1]
[9] Han Bing, Gao Xi-qi, You Xiao-hu. Joint channel estimation and symbol detection for SFBC-OFDM systems via the EM algorithm[J]. IEEE Communication Society, 2004, 6: 3148-3152. [本文引用:1]
[10] He Lan-lan, Ma Shao-dan, Wu Yik-Chung, et al. Joint channel estimation and data detetion for OFDM systems over doubly selective channels[C]∥In Proceedings of the 20th PIMRC, Tokyo, Japan, 2009. [本文引用:1]
[11] D'Andrea A N, Mengali U, Reggiannini R. The modified cramer-rao bound and its application to synchronization problems[J]. IEEE Transactioins on Communication, 1994, 42(2): 1391-1399. [本文引用:1]
[12] Tavares G N, Tavares L M, Petrolino A. On the true cramér-rao lower bound for data-aided carrier-phase-independent frequency offset and symbol timing estimation[J]. IEEE Transaction on Communication, 2010, 58(2): 1378-1387. [本文引用:1] [JCR: 2.418]