引用本文
李阳, 文敦伟, 王珂, 刘乐. 多核学习矩阵化最小二乘支持向量机算法及肺结节识别. 2014, 44(2): 508-515[LI Yang, WEN Dun-wei, WANG Ke, LIU Le. Multiple kernel MtLSSVM and its application in lung nodule recognition. 吉林大学学报(工学版), 2014, 44(2): 508-515]  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
多核学习矩阵化最小二乘支持向量机算法及肺结节识别
李阳1,2, 文敦伟3, 王珂1, 刘乐2
1.吉林大学 通信工程学院,长春 130012
2.长春工业大学 计算机科学与工程学院,长春 130012
3.阿萨巴斯卡大学 计算与信息系统学院,加拿大 艾伯塔 T9S3A3

李阳(1979),女,博士研究生.研究方向:医学图像处理,模式识别,信号与信息处理.

基金:吉林省科技发展计划项目(201201129); 长春工业大学理工科基金项目(2011LG04); 2012年国家级“大学生创新创业训练计划”项目(201210190017); 吉林省教育厅科研专项项目( 2014142);
摘要

针对传统肺结节识别中对感兴趣区域(ROI)进行特征计算时造成的一些隐含结构信息丢失的问题,提出了矩阵输入模式的多核学习矩阵化最小二乘支持向量机识别算法(MKL-MatLSSVM)。该算法将多核方法与矩阵化最小二乘支持向量机(MatLSSVM)相结合,继承了二者优点,涵盖了多种类型的核。为验证算法的有效性,将其应用于肺结节识别。实验采用20个患者的CT图像,提取的ROI中含80个结节及190个假阳。结果表明,MKL-MatLSSVM算法在使用混合核及RBF核时,能兼顾敏感度、准确度和特异度指标,且其接收者操作特征(ROC)曲线下面积均可达到0.96以上,优于先前两种包括MatLSSVM在内的支持向量机(SVM)算法。

关键词: 信息处理技术; 图像识别; 肺结节识别; MKL-MatLSSVM算法; 多核学习; 支持向量机
中图分类号:TP391.4 文献标志码:A 文章编号:1671-5497(2014)2-508-8
Multiple kernel MtLSSVM and its application in lung nodule recognition
LI Yang1,2, WEN Dun-wei3, WANG Ke1, LIU Le2
1.CollegeofCommunicationEngineering,JilinUniversity,Changchun 130012,China
2.CollegeofComputerScienceandEngineering,ChangchunUniversityofTechnology,Changchun 130022,China
3.SchoolofComputingandInformationSystems,AthabascaUniversity,Athabasca,AlbertaT9S3A3,Canada
Fund:
Abstract

Traditional methods for lung nodule recognition need to extract the features of the Region of Interests (ROIs), which usually leads to loss of some implicit structure information. To avoid this problem, a novel Multiple Kernel Learning method based on Matrix Least Square Support Vector Machine (MKL-MatLSSVM) is proposed. This method combines the advantages of both MKL method and MatLSSVM, and supports direct matrix input, suitable for image identification. To verify the effectiveness of the proposed method, it was applied to identify lung nodules in CT images of 20 patients, where the extracted ROIs contain 80 nodules and 190 false positives. The results show that when using hybrid or Radial Basis Function (RBF) kernels in MKL-MatLSSVM, the resulting sensitivity, accuracy and specificity can be balanced, and the area under the Receiver Operating Characteristic (ROC) curve can reach 96%, better than other two previous Support Vector Machine (SVM) methods that include MatLSSVM.

Keyword: information processing; image recognition; lung nodule recognition; MKL-MatLSSVM algorithm; multiple kernel learning; support vector machines
0 引 言

肺结节是肺癌的影像表现形式。模式识别方法已广泛应用于肺结节识别,如贝叶斯分类器[ 1]、人工神经网络[ 2]和支持向量机(Support vector machine,SVM)[ 3, 4]等方法。目前的研究主要采用传统的肺结节识别方法,即首先提取感兴趣区域(Region of interest,ROI)或者感兴趣体(Volume of interest,VOI),然后对ROI或者VOI计算若干特征(包括纹理特征、灰度特征及形态特征等),并将得到的特征值按类别构成特征向量;最后,将特征向量送入分类器得出是否为结节的判断。特征的提取、特征选择算法及由于特征计算而引入的误差直接影响到识别结果。特征过少,识别效果不好;特征过多,容易造成分类器的过拟合。此外,基于特征向量的模式识别还会引起图片中隐含的结构信息丢失。对此,Suzuki等[ 5]提出了基于图像模式的大规模样本神经网络方法,将ROI直接作为样本而省略了特征值计算的繁琐步骤,但是由于神经网络具有对初始权值敏感等特点,限制了其进一步的应用。SVM有效弥补了人工神经网络、贝叶斯分类器等方法中存在的维数灾难、过学习和局部极小等问题。文献[6]提出了结合矩阵化方法和最小二乘支持向量机(Least squares support vector machine,LS-SVM)优点的矩阵模式的最小二乘支持向量机(MatLSSVM)方法,处理二分类问题时,可直接对矩阵模式操作。王青竹[ 7, 8]将矩阵输入模式进一步扩展至三维,用于肺结节VOI识别。文献[6-8]的方法在线性空间对矩阵化SVM方法加以讨论,但未在非线性空间进行具体研究。支持向量机的泛化能力与核函数密切相关,不同的核函数具有不同的优势,提高支持向量机性能的关键,是设计适合给定问题的核函数。

鉴于上述分析,本文提出多核学习矩阵化最小二乘支持向量机算法(Multiple kernel learning method based on matrixing least squares support vector machines,MKL-MatLSSVM),以解决非线性划分及二维输入模式的分类问题。高斯径向基核是局部核函数,学习能力强、泛化性能弱;多项式核是全局核函数,泛化能力强,学习性能弱。兼顾学习能力与泛化能力,以高斯径向基核与多项式核为基本核函数,根据核函数的凸组合定理构造了多核矩阵,设计出MKL-MatLSSVM算法,并应用于肺结节识别。

1 矩阵化LS-SVM(MatLSSVM)
1.1 传统向量输入模式的LS-SVM

传统LS-SVM用于分类时常解决以特征向量为输入的识别问题。输入样本集由l对输入与输出数据构成,可表示为

T={(xi,yi)|i=1,…,l}⊂Rn×{+1,-1} (1)

式中:xi为第i个向量模式的输入;yi为其对应的输出。LS-SVM的原始问题是凸二次规划:

wT w + ,

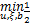
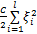
s.t. y i( wT Φ( x i) +b) =1 -ξ i, (2)

i=1,…, l

式中: w为左乘权重向量; ξ i为松弛变量; Φ( x i)为 x i在特征空间的映射; b为常数偏置; C为正则化系数。

引入核函数概念:

K( x i, x j) =Φ( x i)· Φ( x j) (3)

核函数 K( x i, x j)代表 Φ( x i)与 Φ( x j)间的内积,则对应最小二乘支持向量机的决策函数为

f( x) =sign 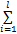α i y i K( x i, x) +b (4)

式中:sign(·)表示符号函数;当 f( x) =1时,将 x分为正类;当 f( x) =-1时,将 x分为负类。

1.2 矩阵输入模式的LS-SVM(MatLSSVM)

传统的LS-SVM在对图像识别时只能处理向量模式的输入,需对图像进行特征计算。当要直接处理图像本身时,则要将其转变或量化成一个向量,可以将图像的像素按照一定规律串联成一个一维向量[ 7]。首先,这种转换可能会遇到小样本问题、过拟合问题及运算复杂度高问题;其次,将图像中的每个像素作为一个独立的点来看待,破坏了图像像素间的空间分布关系,使每一个图像空间的冗余矩阵无法得到充分利用,有关局域及空间关系中的一些信息丢失;最后,浪费了大量的存储空间。对此,Wang等[ 6]将矩阵模式思想引入到LS-SVM算法中,在线性空间中提出了基于矩阵模式的最小二乘支持向量机(MatLSSVM)。训练样本集可以表示为

S={( A i, y i) |i=1,…, l}⊂

×{ +1, -1} (5)

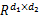
式中: A i为 MatLSSVM算法的第 i( i=1,…, l)个输入样本,为 d1 ×d2维的矩阵,即训练用的图像。而传统的 LS-SVM若直接处理图像,需将矩阵 A i以首尾逐行或逐列串联的形式构造成 d1 d2 ×1维的向量 x i。

MatLSSVM对于原问题可以描述为

wT w +

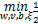
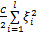
s.t. y i( wT A i v +b) =1 -ξ i(6)

i=1,…, l

l为训练样本的数目。约束式中的 d2维右乘权重向量 v,是为了适应矩阵模式的输入。 w为 d1维左乘权重向量,故 wT A i v为一个常量,至此可以直接对矩阵模式的输入样本进行处理。对应决策函数为

f( A) =sign( wT Av +b) =1, A∈class +1

-1, A∈class -1 (7)

两个权重向量 w和 v及偏置 b可在训练过程中得到,详见文献[6]。

2 多核学习矩阵化最小二乘支持向量机(MKL-MatLSSVM)
2.1 传统LS-SVM的核函数选择

核函数可以与不同算法结合起来,形成基于不同核学习的算法,满足Mercer条件的对称函数可作为核函数。传统支持向量机以向量为输入模式,常用的基本核函数有线性核函数、多项式核函数、高斯径向基核函数(Radial basis function,RBF)依次表示为

K linear( x i, x j) = 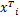x j(8)

Kpoly( x i, x j) =( x j +1) d(9)

Krbf( x i, x j) =exp( -‖ x i - x j‖2 /(2 σ2)) (10)

式中: d为多项式核的阶数; σ为RBF核的宽度,参数 d与 σ需要预先给定。

多项式核函数是全局核函数,而高斯径向基核函数是局部核函数。

传统 LS-SVM以任意两个向量 x i和 x j作为输入时,式(8)(9)(10)得到的结果 K ij = K( x i, x j)为一个数值, l为训练样本数,并且由这些数值最终构成了标准的 l×l维核矩阵 K。

2.2 MatLSSVM的多核学习方法

核函数对于MatLSSVM同样重要,通过核函数的非线性映射,输入空间中线性不可分问题可以转变为高维特征空间中的线性可分问题,以此实现非线性分类。本文提出的MKL-MatLSSVM算法即是在MatLSSVM[ 6]基础上引入核方法,对应于式(3)有下式成立: K( A i, A j) = Φ( A i)· Φ( A j) (11)

根据文献[6],将式(8)(9)(10)的核函数分别作矩阵化处理,以对应二维矩阵(图像)输入模式下的基本核矩阵(12)(13)(14): Klinear( A i, A j) = 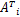A j(12)

Kpoly( A i, A j) =( 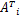A j +ones( d2, d2)) d(13)

Krbf( A i, A j) =exp - 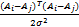] (14)

式中: A i和 A j分别为第 i幅及第 j幅的输入图像,输入图像的尺寸均为 d1 ×d2维矩阵。

观察式(13)不难发现,当多项式阶数 d降为1时,即为线性核函数,与式(12)仅相差一个常数项,故可以认为线性核为多项式核的特例。式(13)中常数项为 d2维方阵,这是因为 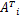A j为 d2 ×d2维,这样做相当于多项式核矩阵中的常数项取1。分析式(12)(13)(14),以任意两幅图像作为输入时, K ij结果为一个 d2维方阵,而不是标准状态下如式(8)(9)(10)所得的常数。很显然要将式(12)(13)(14)转变为标准形式,即将 K ij量化为一个数值,方法为在其两侧用向量 v进行左乘及右乘处理,变为 K ' ij = v t K ij v,则矩阵模式 K ij经变换后得到标准形式 K ' ij,并由 K ' ij构成 l×l维核矩阵 K '。核函数本质上是对应于高维空间中的内积的,从而与生成高维空间的映射一一对应。式(15)证明通过此种变化,可以将矩阵化输入的核矩阵 K ij转化为高维特征空间的内积形式,即标准核矩阵形式 K ' ij。 K ' ij = K '( A i, A j) = vT( A i, A j) v =

v l Φ( A i)T Φ( A j) v =( Φ( A i) v)·( Φ( A j) v) (15)

多核函数可以通过多个基本核函数的凸组合进行构造。对于传统 LS-SVM方法,若 K p(1≤ p≤ M)是基本核函数, m p为各基核所占权重,则由 M个基核构成的多核方法如下:

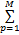
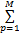
K= m p K p

m p =1, m p≥0 (16)

若干种基核函数的凸组合仍然为核函数。如果基核选取适当,则新核函数 K可以具有更强的泛化能力。

前述矩阵化方法[6 - 8]只在线性空间进行讨论,未将问题扩展至非线性空间,故未充分发挥核方法在 SVM中的优越性。本文将传统 LS-SVM的多核方法推广至矩阵模式,有下式成立: K= 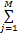β j K j(17)

β j =1, β j≥0

式中: M为组合成多核矩阵基本核的个数; β j为各个基核所对应的权系数。

容易验证,上述多核矩阵经过标准化处理(即 K ' ij = vT K ij v)满足 Mercer条件,可以用于 SVM的训练与分类。

2.3 MKL-MatLSSVM方法概述

本文提出的MKL-MatLSSVM方法其训练样本集与MatLSSVM相同,可以用式(5)表示。原问题的描述与传统LS-SVM类似:

wT w + ,

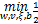
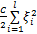
s.t. y i( wT Φ( A i) v + b) =1 -ξ i(18)

i=1,…, l

式(18)中约束条件是二次的,这是由于 w和 v均未知。 MatLSSVM采用的是线性核函数,对应式(18)有 Φ( A i) = A i。与传统的 LS-SVM的原问题式(2)相比,式(18)多了右乘权重向量 v,这是为了处理二维矩阵的输入,使矩阵化输入的核矩阵 K ij转化为标准核矩阵形式 K ' ij。由式(18)可构造拉格朗日方程:

L( w, v, b, ξ, α) = wT w + -

α i[ y i( wT Φ( A i) v +b) -1 +ξ i](19)

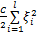
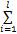
式中: α i为拉格朗日乘子; C为正则化系数; ξ i为松弛因子。

根据 KKT条件,有:

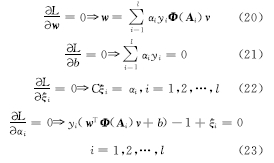
由式(20)可知, w和 v是相互依赖的,因此不可能同时进行 w和 v最优解的计算。固定 v,消去 w和 ξ i,得到式(24),通过式(24)可以解得 b和 α i:

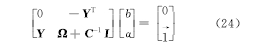
式中: Y =[ y1,…, y l]T为输出的类标签; 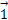=[11,…,1 l]T为长度为 l的全1列向量; Ω ij =y i y j vT K( A i, A j) v[ 6],这里需预设 v的初始值 v1, K( A i, A j)即为2 .2节所述的非标准形式多核矩阵。 w、 v分别通过式(25)(26)更新, η是学习率,下标 t是迭代次数。

w t = 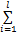α i y i Φ( A i) v t(25)

v t+1 = v t -η = v t -η- α i y i Φ( ) w t (26)

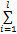
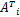
令 B = Ω + C -1 I,函数偏移常量 b为

b=

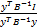(27)

对应于输入矩阵 Z的决策函数为

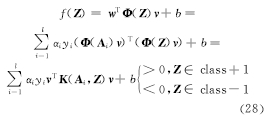
在计算复杂度方面,矩阵输入模式的 w与 v常需要经过多次迭代计算得到,当迭代次数 t>maxIter或者‖ v t+1 - v t‖≤ ε,输出最终右乘向量 v,并对待测矩阵 Z进行判别分类。其中,maxIter是最大迭代次数。

3 实验结果与分析
3.1 实验数据集的描述

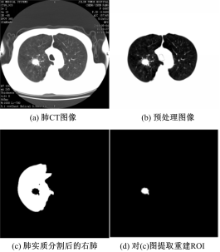
实验所用数据来源于吉林省某三甲医院的20套CT图像,并配有医生的诊断结果。将CT图像经过预处理、支气管添堵与小血管移除、肺实质分割及左右肺分开等处理,并经过圆点滤波器增强后,提取出孤立型候选结节的ROI[ 7]。图1给出了ROI提取的具体步骤。20套CT影像序列中共提取出80个结节,190个假阳,这是由于圆点滤波器并不能滤除血管交叉点和血管端点结构。ROI提取(见图1(d))是在肺实质分割(见图1(c)) :

图1 提取ROI步骤Fig.1 ROI extraction steps

上进行的,可以保证ROI都是在肺实质内。整幅影像面积为512×512像素,肺实质区域的面积大约为100×200像素[ 9]。每个像素的面积约为0.6 mm×0.6 mm,结节定义为肺实质内直径在3~30 mm的类圆形致密影,根据计算,结节大约用50×50的像素表示即可。为了使所有结节甚至肺癌的小病灶区域都可以包括在内,采用90×90的矩阵足够表示每个结节的ROI(包括较大病灶及疑似区域)。将ROI用90×90的矩阵表示,是由于ROI本身在肺实质区域内,而其面积远小于肺实质区域,更小于整幅图像的面积,故检测算法只需作用于ROI而无需处理整幅图像或整个肺实质区域,从而提高计算速度。将前面提取的ROI以几何中心对齐的方式移至90×90矩阵的中心。例如,若一幅图像尺寸为512×512,而ROI的尺寸仅为30×41,则应将30×41的像素赋给90×90矩阵的第31~60行,第26~66列,90×90矩阵以点(45,45)为中心。本文将通过多核学习持向量机方法对提取出的ROI(90×90)进行识别。

考虑计算复杂度和仿真时间,在保证结果稳定的前提下,将提取的ROI分为3组:随机选取20个结节和20个假阳用于构成训练集,可以保证计算的速度与所需数据量的要求;20个结节和50个假阳构成了参数集,用于寻找最优参数组;其余40个结节和120个假阳构成了测试集。本文并未采取交叉验证方法,是由于向量 v和向量 u在每一折时,都需重新初始化,并经过若干次迭代而更新,若进行十折交叉验证,则 v、 u一共存在10种迭代后的结果,无法保证哪一种更优。矩阵化输入还会带来计算复杂度的大规模增加及训练时间的延长。为此,实验将用专门的参数集来保证选取结果的稳定性。

肺结节识别优先考虑不漏检,用敏感度指标表示[ 3]。在此前提下尽量保证总体的识别指标,用准确度衡量。此外,特异度是被正确诊断为阴性的比例。在参数选取过程中,(20 +20)的数据用于建立 MKL-MatLSSVM算法的训练集,并保证梯度下降。参数寻优部分根据参数集得到的敏感度指标与准确度指标来选取最优参数组。测试阶段用得到的最优参数组对测试集进行识别。准确度、敏感度、特异度指标依次用 ACC、 SEN、 SPE表示

ACC=

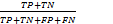(29)

SEN=

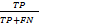(30)

SPE=

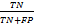(31)

式中:TP为检测出的真阳性结节;FP为检测出的假阳性结节;FN为未检测出的真阳性结节,即假阴性;TN为检测出的非结节,即真阴性。

3.2 MKL-MatLSSVM参数选取及结果分析

本文选取多项式核、RBF核为基本核函数,以式(17)构造矩阵化多核方法,如下式所示:

K( A i, A j) =βKrbf +(1 -β) Kpoly =

βexp - ]+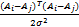

(1 -β){[( 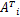A j) +ones( d2, d2)] d}

0≤ β≤1 (32)

为包含尽量多的基核函数,令 d={1,2,3},将线性核也考虑进来( d=1),因为线性核与任意非线性核的组合,也将是非线性多核函数。取0≤ β≤1,以0 .1的长度步进,将多个单核函数凸组合作为多核函数。参数选取不同时,本文的多核函数可分为以下情况: ①β=0且 d≠1时,多核函数特殊化为多项式核; ②β=1时,多核函数特殊化为 RBF核; ③β=0且 d=1时,多核函数特殊化为线性核; ④0 <β<1时,多核函数特殊化为混合核,混合核又可分为 RBF核与多项式核的组合及 RBF核与线性核的组合。考虑以图像作为输入的计算量及运行时间,初始化迭代次数 maxIter=500。参数选取采用穷尽式的网格搜索方法,松弛变量取 ξ=0 .001。右乘向量 v可任意初始化,令 v1 =[1,…,1,…,1]T,经过第 t(1≤ t≤maxIter)次迭代后,根据式(25)(26)求得 v与 w。 w的更新需预知映射 Φ(·)的具体形式,这成为了一个瓶颈。为此,文中采用线性核得到的最优 v *代替,并认为测试前已得到最优矢量 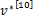。这样做,其一,不需知道 Φ(·)的具体形式;其二, v固定可以得到非线性方法时 v的局部最优解;其三, v *是经过梯度下降方法得到的最优值,有效降低了计算复杂度并保证输入单元的相似性。 学习率 η从{0 .5,1,10,100,1000}中选择, η取值影响梯度下降的速度及程序运行时间, η增加则梯度下降变快。正则化系数 C及 RBF核宽度 σ的选取采用网格搜索法,均从2 -8开始,通过乘以2更新,至28结束。取梯度阈值ε =0 .001。 MKL-MatLSSVM算法的步骤如下:

Step1 初始化矢量 v1,给定 C、 η、maxIte r、 ε,并令 t=1。

Step2 令 Φ( A i) = A i,通过式(18) ~(26)求解 w t及 v t+1。

Step3 若 t≤maxIter或者‖ v t+1 - v t‖ >ε,则令 t=t+1,转至 Step2,否则输出对应 C值的 v *, w *。

Step4 将对应 C值的 v *与 w *代入式(18)。

Step5 通过参数的调整选取不同的核函数,根据式(24)求解原始问题(18)。

Step6 通过式(27)求b。

Step7 通过式(28)对待测矩阵样本 Z进行分类。

表1列出了 MKL-MatLSSVM方法中涵盖的所有核对应的最优参数组及利用最优参数组得到的测试指标。

参数选取以在参数集上得到的 SEN最大且 ACC也较大所对应参数组为最优参数组,可能有若干组参数同时达到最优。参数寻优阶段,当寻到最优参数组后,对参数 β进行网格精细搜索,使 β在所得结果基础上,按照0 .01的网格精度进一步寻优,以保证结果精确。表1中混合核情况分为 RBF核与多项式核的组合(对应混合核参数组表

表1 不同核的比较 Table 1 Comparison between different kernels

①②)及RBF核与线性核的组合(对应混合核参数组③④)分别得到两组最优参数。

当参数选取不同时,提出的MKL-MatLSSVM方法涵盖了混合核、线性核、多项式核及RBF核情况。由表1可见,线性核在参数寻优阶段共找到两组达到最优指标的参数组,用其对测试集进行最终测试时,参数组①所得结果较好,SEN=85%,ACC=80.63%,SPE=79.17%,但总体来看3个指标均较低。多项式核学习的能力不强,结果仅能达到SEN=70%,ACC=71.88%,SPE=72.5%,3个指标均不好。RBF核在进行结节检测时效果最优,表现较稳定,7组参数得到的指标均较高。在参数寻优过程中RBF核共找到了7组符合条件的参数组,其中参数组④最终的测试指标SEN可达95%,ACC可达90.63%,SPE也可达到89.17%,基本可以做到不漏检,准确率较高。RBF核的结果较理想,这可能与结节本身的似圆性有关,因为MKL-MatLSSVM方法是以候选结节的ROI图像作为输入的。当以混合核为核函数时,混合核的①②两个参数组对应 d=2,即RBF核与多项式核的组合,3个指标并不理想。混合核的③④两个参数组,对应 d=1,为线性核与RBF核的混合,从参数 β的取值,可以看到RBF核占据了主体地位,最终测试阶段,SEN可达90%,ACC可达93.13%,SPE可达94.17%。MKL-MatLSSVM算法的混合核情况与RBF核情况相比,SEN降低了5%,但ACC提高了2.5%,SPE提高了5%,两种情况各有所长。综上可见,RBF核做核函数与混合核做核函数的形式都具有一定优势。实验还发现,当多项式阶数 d≥3时,混合核的学习能力明显变差。

将MKL-MatLSSVM算法的几种情况与文献[6]算法、文献[4]算法比较,各算法所得最优结果如表2所示:

表2 各种算法的检测结果 Table 2 Comparison between different algorithms

文献[6]算法(MatLSSVM,即线性核[ 6])为本文提出的MKL-MatLSSVM算法的一个特例。由表2可见,MKL-MatLSSVM算法的混合核情况与文献[6]算法相比,SEN提高了5%,ACC提高了12.5%,SPE提高了15%。MKL-MatLSSVM算法的RBF核与线性核相比,SEN、ACC、SPE每个指标均提升10%。文献[4]算法采用特征向量作为输入模式,用libsvm工具箱进行仿真。参数选取原则与本文一致,即优先考虑SEN。由所得结果可以看出,测试集的SEN可以达到97.5%,在各类算法中最高,而ACC指标此时仅为78.75%,在各类算法中则最低,各个指标很难兼顾。

就SEN指标而言,文献[4]算法最优,本文的RBF核算法与混合核算法次之,文献[6]算法效果不理想;就ACC指标而言,混合核与RBF核效果最优,文献[6]算法次之,文献[4]算法不理想。综合3个指标,仅有提出的混合核方法在最终测试阶段均达到了90%以上,提出的RBF核也较为理想,且重点考核的ACC和SEN指标均较理想。训练阶段,线性核参数最少,RBF核参数较多,混合核情况的参数最多,所需训练及参数寻优时间较长。可见,MKL-MatLSSVM方法所得结果的优越性是以牺牲计算复杂度和计算时间换取的。但当最优参数组确定后,测试时间均在5 s以内,可以被医生接受。几种算法的接收者操作特征(Receiver operating characteristic,ROC)曲线如图2所示:

图2 ROC曲线Fig.2 ROC curve

ROC曲线下对应面积如下:文献[6]算法为0.8487,文献[4]算法为0.8842,混合核和RBF核分别为0.9612和0.9685。可见,RBF核及混合核的曲线下面积均可达到0.96以上,其中RBF核情况比混合核情况略好,面积多出0.0073,比文献[4]算法多出0.0843,比文献[6]算法多出0.1198。结果进一步表明,MKL-MatLSSVM算法的有效性。

4 结束语

提出了多核学习矩阵化最小二乘支持向量机(MKL-MatLSSVM)算法,其中包含RBF核、多项式核、线性核以及混合核4种情况,可直接处理图像形式的输入,并将该算法应用于肺部结节识别。该方法由RBF核与多项式核(含线性核)以加权形式构成多核矩阵,兼顾了核方法与支持向量机的优点,将问题拓展至二维矩阵输入模式的非线性分类。用提取出的感兴趣区域的图像代替特征作为输入,一方面减少了因特征提取而造成的信息损失,另一方面则只对感兴趣区域进行识别分析,减少计算量。实验结果表明,本文提出的算法兼顾准确度、敏感度和特异度3个指标,在各个指标的综合选取方面,优于MatLSSVM方法。提出的混合核方法及RBF核方法,虽然所需估计参数多于线性核情况,计算复杂度稍高,但最优参数确定后,测试时间在医生可接受范围内。需要说明的是,实验仅针对孤立型肺结节进行识别,但多核矩阵方法可以推广至粘连肺壁型结节等多种类型结节的识别,且不局限于肺部结节识别。

鉴于RBF核的表现,矩阵化输入的多尺度核的构造、矩阵奇异性问题及参数组快速寻优将作为下一步工作目标。

The authors have declared that no competing interests exist.

参考文献
[1] Farag A, Ayman E B, Gimel F G, et al. Detection and recognition of lung nodules in spiral CT images using deformable templates and Bayesian post-classification[C]∥International Conference on Image Processing(ICIP 2004), Singapore, 2004. [本文引用:1]
[2] Kenji S, Li F, Sone S, et al. Computer-aided diagnostic scheme for distinction between benign and malignant nodules in thoracic low-dose CT by use of massive training artificialneural network[J]. IEEE Transactions on Medical Imaging, 2005, 24(9): 1138-1150. [本文引用:1] [JCR: 4.027]
[3] 孙申申, 任会之, 康雁, 等. 基于遗传算法和支持向量机的肺结节检测[J]. 系统仿真学报, 2011, 23(3): 497-501, 566.
Sun Shen-shen, Ren Hui-zhi, Kang Yan, et al. Lung nodule detection by GA and SVM[J]. Journal of System Simulation, 2011, 23(3): 497-501, 566. [本文引用:2] [CJCR: 0.914]
[4] 张婧, 李彬, 田联房, 等. 结合规则和SVM方法的肺结节识别[J]. 华南理工大学学报: 自然科学版, 2011, 39(2): 125-129, 147.
Zhang Jing, Li Bin, Tian Lian-fang, et al. Lung nodule recognition combining rule-based method and SVM[J]. Journal of South China University of Technology (Natural Science Edition), 2011, 39(2): 125-129, 147. [本文引用:1]
[5] Suzuki K, Armato S G, Li F, et al. Massive training artificial neural network (MTANN) for reduction of false positives in computerized detection of lung nodules in low-dose computed tomography[J]. Med Phys, 2003, 30(6): 1602-1617. [本文引用:1] [JCR: 2.911]
[6] Wang Z, Chen S C. New least squares support vector machines based on matrix patterns[J]. Neural Processing Letters, 2007, 26(1): 41-56. [本文引用:4] [JCR: 1.24]
[7] 王青竹. 基于三维SVMs的肺部CT中的结节检测算法[D]. 长春: 吉林大学通信工程学院, 2011.
Wang Qing-zhu. Detection of lung nodules in CT images based on 3D SVMs[D]. Changchun: College of Communication Engineering, Jilin University, 2011. [本文引用:3]
[8] Wang Q Z, Kang W W, Wu C M, et al. Computer-aided detection of lung nodules by SVM based on 3D matrix patterns[J]. Clinical Imaging, 2013, 37(1): 62-69. [本文引用:2] [JCR: 0.648]
[9] 孙申申. 基于CT影像的肺结节检测与分割方法研究[D]. 沈阳: 东北大学信息科学与工程学院, 2009.
Sun Shen-shen. Lung nodule detection and segmentation methods based on CT images[D]. Shenyang: School of Information Science & Engineering, Northeastern University, 2009. [本文引用:1]
[10] 皋军. 智能识别中的降维新方法及其应用研究[D]. 无锡: 江南大学信息工程学院, 2010.
Gao Jun. The study of novel dimensionality reduction methods and application in intelligent recognition[D]. Wuxi: School of Information Engineering, Jiangnan University, 2010. [本文引用:1]