引用本文
王佳, 胡侠, 解相鹏. 带有执行器故障的离散时间T-S模糊系统可靠控制. 2014, 44(2): 554-559[WANG Jia, HU Xia, XIE Xiang-peng. Reliability control for discrete-time T-S fuzzy systems with actuator faults. 吉林大学学报(工学版), 2014, 44(2): 554-559]  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
带有执行器故障的离散时间T-S模糊系统可靠控制
王佳1, 胡侠2, 解相鹏3
1.北京理工大学 机械与车辆学院, 北京 100081
2.上海汽车集团股份有限公司 乘用车分公司,上海 201804
3.东北大学 信息科学与工程学院,沈阳 110004

王佳(1981),男,高级工程师,博士研究生.研究方向:容错控制,故障诊断.

基金:国家自然科学基金项目(60904017,61273027);
摘要

针对带有执行器故障的离散时间T-S模糊系统的可靠控制问题提出了一种可靠控制器设计方案。与已有带有执行器故障的离散时间T-S模糊系统的可靠控制器相比,本文设计的可靠控制器采用了不同的控制架构,从而引入更多控制增益矩阵变量,并且在主要结果证明过程中提出了一种附加变量引入技术,上述措施显著降低了已有结果的保守性。此外,所得到的可靠控制器设计条件是以线性矩阵不等式形式给出的,可以很方便地通过标准数值计算软件来进行求解。最后,仿真实验结果验证了本文所提出的可靠控制器的有效性。

关键词: 自动控制技术; 执行器故障; 非线性系统; 可靠控制; 模糊系统
中图分类号:TP202 文献标志码:A 文章编号:1671-5497(2014)2-554-6
Reliability control for discrete-time T-S fuzzy systems with actuator faults
WANG Jia1, HU Xia2, XIE Xiang-peng3
1.School of Mechanical and Vehicular Engineering, Beijing Institute of Technology, Beijing 100081, China
2.SAIC Motor Corporation Limited Passenger Vehicle Co., Shanghai 201804, China
3.School of Information Science and Engineering, Northeastern University, Shenyang 110004, China
Fund:
Abstract

The problem of reliable control of discrete-time T-S fuzzy systems with actuator faults is investigated and the design scheme of a reliable controller is proposed. Compared with the existing reliable controllers, different control structures are adopted in the proposed reliable controller, which can introduce more control gain matrices, and a method for introducing additional variable is also applied in the proof of the main result. Therefore, the conservatism of the existing results could be obviously reduced on account of the underlying measures. Furthermore, the obtained reliable control conditions are given in terms of linear matrix inequalities, which could be easily solved via standard numerical software. Finally, the effectiveness of the proposed approach is illustrated by means of numerical experiments.

Keyword: automatic control technology; actuators faults; nonlinear systems; reliable control; fuzzy systems

中图分类号:TP202 文献标志码:A 文章编号:1671-5497(2014)2-554-6

在实际工业生产过程中控制系统执行器失效现象经常发生,因此针对带有控制器失效控制系统的可靠控制器设计问题引起了很多研究者的注意[1,2,3],但其主要目标是为带有执行器故障的线性系统设计出一种固定增益参数控制器,它可以保证执行器在部分失效情况下整个控制系统的稳定性。对于带有执行器故障的非线性系统,已有学者通过基于T-S模糊模型的方法进行了可靠控制器设计的相关研究,并取得了较好的成果[4,5,6]。

另一方面,T-S模糊模型作为研究复杂非线性动态系统的一种强有力的工具,已被成功应用于多个实际控制系统设计中[7,8,9,10]。早期的研究成果大多数采用文献[7]提出的并联分布补偿控制律(简称为PDC控制律)进行基于T-S模糊模型的非线性系统控制器设计。但这种PDC控制律得到镇定控制条件通常保守性非常大,很大程度上限制了T-S模糊模型在相关领域的应用。2004年,法国著名控制学者Guerra针对离散时间T-S模糊系统控制问题提出了著名的非并联分布补偿控制律(简称为非-PDC控制律)[11]。这种非-PDC控制律通过改变控制器架构引入了更大的设计自由度,大大减少了控制设计的保守性。近几年,基于非-PDC控制律的设计思想,学者们设计出了保守性越来越小的镇定控制条件[12,13,14,15,16]。

本文针对带有执行器故障的离散时间T-S模糊系统的可靠性控制问题提出了一种控制器设计方案。该方案通过采用不同的控制架构,降低了控制设计的保守性,并通过仿真实验予以了验证。

1 系统描述与数学引理
1.1 带有执行器故障的离散时间T-S模糊系统

考虑如下形式的带有执行器故障的离散时间T-S模糊系:

x( k+1) =

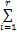(1)
h i( θ( k))

式中: x( k)为 n维系统状态向量; u( k)表示 m维系统执行器向量; A i和 B i为适当维数的系统参数矩阵; h i( θ( k))为模糊隶属函数; r为模糊模型规则数; w L为表示执行器发生故障的标识矩阵。

对于标识矩阵 w L,其组成结构形式为

w L∈ Ω=

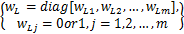(2)

式中:若 w Lj =0则表示第 j个执行器发生故障。因此,对于具有 m个执行器的系统,执行器发生故障的可能情况有2 m -1种,也就是说,集合Ω中由2m-1个矩阵组成,因而有L=1,2,…,2m-1。

定义1[11] 如果在所有 w L∈ Ω情况下带有执行器故障的离散时间 T-S模糊系统(1)都是全局渐近稳定的,那么就可以说带有执行器故障的离散时间 T-S模糊系统(1)是可靠稳定的。

1.2 新型可靠控制器设计及数学引理

为了保证带有执行器故障的离散时间T-S模糊系统(1)的可靠稳定,文献[6]基于PDC技术提出了一种状态反馈控制律 u( k) = 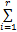h i( θ( k)) K i x( k),得到了基于线性矩阵不等式条件的控制设计条件。客观地讲,文献[6]中的结果仍然存在较大保守性。为了进一步减少已有结果的保守性,本文提出了如下一种新型可靠控制器:

与文献[6]中使用的状态反馈控制律相比,本文提出的新型可靠控制器(3)具有全新的控制架构,能够引入更多控制增益矩阵 F ij和 G i。特别是为了配合这种全新的控制架构,在本文主要结果证明过程中设计了一个与之匹配的李亚普诺夫函数。通过上述措施的实施,显著增加了可靠控制设计的自由度,并获得保守性更小的可靠控制器设计条件。

引理1[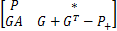11] 对于对称正定矩阵 P >0和 P + >0,矩阵不等式 AT PA - P <0成立的一个充分条件是存在一个适当维数矩阵使得如下矩阵不等式成立: >0。

2 主要结果

定理1 对于带有执行器故障的离散时间 T-S模糊系统(3),若存在适当维数对称矩阵 P iL,适当维数矩阵 F ij, G i( w L∈ Ω; L=1,2,…,2 m -1; i=1,2,…, r; i≤ j),适当维数对称矩阵 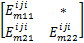(i=1,2,…,r;j=1,2,…,r;m=1,2,…,r),

适当维数的矩阵

(i=1,2,…,r;1≤j

使得如下一组线性矩阵不等式成立:

+

>0,

i=1,2,…, r; m=1,2,…, r(4)

+

+

+

+ >0,

i=1,2,…, r-1; i≤ r; m=1,2,…, r(5)

+

+

+

+ >0,

i=1,2,…, r-1; i≤ r; m=1,2,…, r(6)

+

+ +

+

+ +

+

+ >0,

i=1,2,…, r-2; i≤ r; m=1,2,…, r(7)

<0,

i=1,2,…, r; m=1,2,…, r(8)

那么,带有执行器故障的离散时间 T-S模糊系统(1)在新型可靠控制器(3)的控制下对于所有 w L∈ Ω是可靠稳定的。

证明 对在新型可靠控制器(3)的控制下的带有执行器故障的离散时间 T-S模糊系统(1)考虑如下形式的李亚普诺夫函数:

V L( x( k)) = x( k)T P zL x( k)(9)

式中:

P zL = h i( θ( k)) P iL; G z = h i( θ( k)) G i。

对上述李亚普诺夫函数沿时间方向求取一阶差分,可得:

V L( x( k)) = x( k)T( Π- P zL ) x( k)(10)

式中:

Π= P zL+ ( A z + B z F z )。

于是,根据李亚普诺夫稳定性定理,带有执行器故障的离散时间 T-S模糊系统(1)对于所有 w L∈ Ω是可靠稳定的充分条件为如下矩阵不等式成立:

Π- P zL <0(11)

对矩阵不等式(11)两边分别左乘和右乘 和 G z,可得与之等价的矩阵不等式:

( A z G z + B z F z)T P zL+ ( A z G z + B z F z) - P zL <0,(12)

由引理1可知,若下述矩阵不等式成立可以保证矩阵不等式(12)

成立:

>0(13)

式中: P zL+ = h i( θ( k+1)) P Li;

G z+ = h i( θ( k+1)) G i。

另一方面,重新组织不等式(13)左侧矩阵的表示形式,可得:

=

式中: h i =h i( θ( k)); Ξ mL = G m + - P mL。

于是,若线性矩阵不等式(4) ~(7)成立,则有:

接下来,对线性矩阵不等式(8)两边分别左乘 和右乘 可得:

于是,结合矩阵不等式(14)和(16),容易看出若线性矩阵不等式(4) ~(8)成立,则矩阵不等式(13)亦成立;换句话说,带有执行器故障的离散时间 T-S模糊系统(1)在新型可靠控制器(3)的控制下对于所有 w L∈ Ω是可靠稳定的。

证毕。

注释1 通过改变李亚普诺夫函数的构造和提出一种新颖的附加变量引入技术,我们在定理1中给出了保守性更小的执行器故障的离散时间 T-S模糊系统(1)的新型可靠控制器设计条件。特别地,附加变量的引入将各个模糊子模型之间的耦合关系映射到若干个大矩阵(8)中,能够更加有效地考虑模糊隶属函数的有用信息,减少可靠控制器设计的保守性。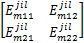

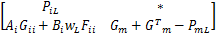
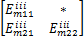
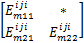
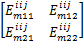
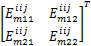
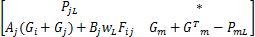
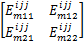
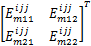
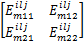
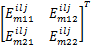
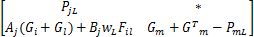
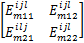
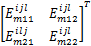
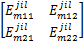
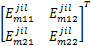
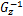
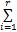
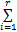
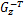
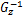
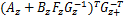
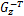
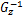
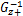
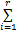
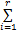
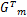
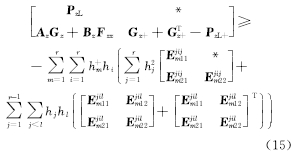
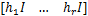
3 仿真研究

考虑如下形式的离散时间非线性控制系统:

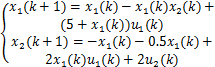
由模糊建模方法,令 θ1( k) =( β+ x1( k)) /(2 β)和 θ2( k) =( β- x1( k)) /(2 β),则上述非线性系统可由如下 T-S模糊系统来表示:

=

h i

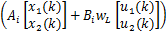
式中: h1 =θ1( k); h2 =θ2( k);

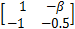
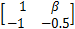
A1 = ; A2 = ;

B1 = 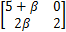; B2 = 。

在实际应用中,上述系统中两个执行器输入量 u1( k)和 u2( k)均可能发生执行器故障,因此执行器发生故障的标识矩阵 w L具有2种可能的取值形式:

w L = ( u1( k)失效)

w L = ( u2( k)失效)。

为了验证本文所提方法的有效性,我们在仿真中分别利用文献[6]中的方法和本文定理1提出的方法进行可靠控制器的设计。特别地,为了验证本文提出的附加变量引入技术的有效性,我们在应用定理1时分两种情况使用: ①不使用附加变量引入技术,表示为定理1( *); ②使用完整的定理1提出的可靠控制器设计方法,表示为定理1( **)。由上述三种方法得到的可控 β最大值的计算结果为:文献[6]中提出的方法只能在 β≤1 .68时才能设计出可行的可靠控制器,以保证上述带有执行器故障的离散时间 T-S模糊系统对于所有 w L∈ Ω情况是可靠稳定的;与之相比,用定理1( *)得到的结果是 β≤1 .72,可以看出本文提出的新型可靠控制器在减少保守性方面的有效性;进一步定理1( **)所得到的结果是 β≤1 .78,证明了本文提出的附加变量引入技术能够进一步减少结果的保守性。

选择定理1( **)(β =1 .78)的方案,利用 Matlab计算软件可以计算出满足线性矩阵不等式(4) ~(8)条件下的控制增益矩阵 F11, F12, F22, G1和 G2。

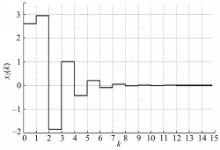
不失一般性,在本文仿真中设定执行器 u2( k)发生了故障,即有 w L = 。对于给定系统初始状态条件: x1(0) =-1 .80和 x2(0) =2 .60,图1和图2分别给出了由方法定理1( **)所得到的可靠控制器(3)的控制下系统状态 x1( k)和 x2( k)的轨迹图,图3给出了未失效的执行器控制输出量 u1( k)的轨迹图。由图1 ~图3可以看出,虽然系统发生了执行器控制输出量 u2( k)的失效故障,但整个闭环系统仍然能保证全局渐近稳定,证明了本文所提出方法的有效性。

图1 状态变量 x1( k)的轨迹图Fig.1 The trajectory of the state variable x1( k)

图2 状态变量 x2( k)的轨迹图Fig.2 The trajectory of the state variable x2( k)

图3 控制输出量 u1( k)的轨迹图Fig.3 The trajectory of the control input u1( k)

4 结束语

通过对可靠控制器的架构进行全新设计,针对带有执行器故障的离散时间T-S模糊系统可靠控制问题提出了一种新型的可靠控制器设计方案。这种新型可靠控制器能够引入更多控制增益矩阵从而增加控制设计的自由度。在主要结果证明过程中还提出了一种新颖的附加变量引入技术,它能够将各个模糊子模型之间的耦合关系映射到若干个大矩阵中,更加有效地考虑模糊隶属函数的有用信息,进一步减少了可靠控制器设计条件的保守性。最后,仿真研究验证了本文所提出方法的有效性。

The authors have declared that no competing interests exist.

参考文献
[1] Zhao Q, Jiang J. Reliable state feedback control system design against failures[J]. Automatica, 1998, 34(10): 1267-1272. [本文引用:1] [JCR: 2.919]
[2] Liao F, Wang J L, Yang G H. Reliable robust flight tracking control: an LMI approach[J]. IEEE Transactions on Control Systems Technology, 2002, 10(1): 76-89. [本文引用:1] [JCR: 2.0]
[3] Yang G H, Wang J L, Soh Y C. H∞ controller design for linear systems[J]. Automatica, 2001, 37(5): 717-725. [本文引用:1] [JCR: 2.919]
[4] Wu H N. Reliable LQ fuzzy control for nonlinear discrete-time systems via LMIs[J]. IEEE Transactions on Systems, Man and Cybernetics, 2004, 34(2): 1270-1275. [本文引用:1]
[5] Wu H N. Reliable LQ fuzzy control for nonlinear continuous-time systems with actuators faults[J]. IEEE Transactions on Systems, Man, and Cybernetics, 2004, 34(4): 1743-1752. [本文引用:1]
[6] Wu H N, Zhang H Y. Reliable H∞ fuzzy control for a class of discrete-time nonlinear systems using multiple fuzzy Lyapunov functions[J]. IEEE Transactions on Circuits and Systems-II: Express Briefs, 2007, 54(4): 357-361. [本文引用:1] [JCR: 1.41]
[7] Wang H O, Tanaka K, Griffin M F. An approach to fuzzy control of nonlinear systems: stability and design issues[J]. IEEE Transactions on Fuzzy Systems, 1996, 4(1): 14-23. [本文引用:1] [JCR: 5.484]
[8] Kim E, Lee H. New approaches to relaxed quadratic stability condition of fuzzy control systems[J]. IEEE Transactions on Fuzzy Systems, 2000, 8(5): 523-534. [本文引用:1] [JCR: 5.484]
[9] Liu X D, Zhang Q L. New approaches to controller designs based on fuzzy observers for T-S fuzzy systems via LMI[J]. Automatica, 2003, 39(9): 1571-1582. [本文引用:1] [JCR: 2.919]
[10] Montagner V F, Oliveira R C L F, Peres P L D. Convergent LMI relaxations for quadratic stabilizability and H∞ control of Tanaki-Sugeno fuzzy systems[J]. IEEE Transactions on Fuzzy Systems, 2009, 17(4): 863-873. [本文引用:1] [JCR: 5.484]
[11] Guerra T M, Vermeiren L. LMI-based relaxed nonquadratic stabilization conditions for nonlinear systems in the Takagi-Sugeno's form[J]. Automatica, 2004, 40(5): 823-829. [本文引用:3] [JCR: 2.919]
[12] Kruzewski A, Wang R, Guerra T M. Nonquadratic stabilization conditions for a class of uncertain nonlinear discrete time TS fuzzy models: a new approach[J]. IEEE Transactions on Automatic Control, 2008, 53(2): 606-611. [本文引用:1] [JCR: 2.718]
[13] Ding B C. Poly-quadratic stability of discrete-time nonlinear systems in Takagi-Sugeno form[J]. Asian Journal of Control, 2009, 11(6): 610-619. [本文引用:1] [JCR: 1.411]
[14] Lee D H, Park J B, Joo Y H. Improvement on nonquadratic stabilization of discrete-time Takagi-Sugeno fuzzy systems: multiple parameterization approach[J]. IEEE Transactions on Fuzzy Systems, 2010, 18(2): 425-429. [本文引用:1] [JCR: 5.484]
[15] Mozelli L A, Palhares R M, Avellar G S C. A systematic approach to improve multiple Lyapunov function stability and stabilization conditions for fuzzy systems[J]. Information Sciences, 2009, 179(10): 1149-1162. [本文引用:1] [JCR: 3.643]
[16] Zhang H G, Xie X P. Relaxed stability conditions for continuous-time T-S fuzzy-control systems via augmented multi-indexed matrix approach[J]. IEEE Transactions on Fuzzy Systems, 2011, 19(3): 478-492. [本文引用:1] [JCR: 5.484]