付尧(1986),男,博士研究生.研究方向:汽车传动系统理论与控制.E-mail:fuy.jlu@163.com
针对减速制动工况下,自动变速车辆的两参数换档策略不能适应驾驶员意图及行驶环境变化、不能有效利用发动机辅助制动的情况,在分析发动机辅助制动作用必要性的前提下,综合考虑了驾驶员意图及行驶环境信息,提出了一种以制动时间、车辆负荷度、制动减速度及车速等参数为输入的基于模糊推理的档位决策方法。道路试验结果表明:该控制策略能够适应驾驶员意图及行驶环境变化,有效地利用了发动机辅助制动,提高了自动变速车辆的行驶安全性。
Automatic transmission shift schedule with two parameters of the vehicle cannot adapt to the driver's intentions and change of driving conditions, and is unable to effectively use engine assisted braking in deceleration brake conditions. Based on the analysis of the necessity of engine assisted braking, a method of gear position decision is proposed, which is based on the fuzzy inference of braking duration, loads, braking deceleration, velocity. This method considers the driver's intentions and the external environment. Road tests indicate that the control strategy could adapt to the driver's intention and the external driving environment. The engine assisted braking can be used effectively. The control strategy improves driving safety of automatic transmission vehicle.
自动变速技术在减轻驾驶员驾驶操作强度的同时,有效地提高了整车动力性、燃油经济性、乘车舒适性,并降低了排放污染。传统的自动变速控制系统以车速和油门开度作为换档控制参数,很难在复杂多变的工况下适应驾驶员的真实意图。制动工况是车辆行驶过程中的典型工况,根据驾驶员制动意图,可将制动工况分为减速制动和停车制动两种[ 1]。减速制动工况下驾驶员一般采取点刹或持续轻踏制动踏板[ 2],使车速维持在驾驶员可接受的安全范围。减速制动工况下的档位决策会影响车辆的行驶安全性及舒适性。传统换档策略在制动工况下退化为单参数换档策略,有两个主要缺点:①由于刹车引起车速的改变以及驾驶员松油门时的跳变,传统换档策略容易出现意外换档问题[ 2];②仅依靠车速作为换档决策参数的换档策略不能依据驾驶员及环境需求有效利用发动机进行辅助制动,在下长坡、雨雪路面及高车速减速制动工况下,有一定的安全隐患。
一些学者对发动机辅助制动以及制动工况相关控制策略进行了研究。文献[ 3, 4, 5]对发动机辅助制动的机理及其对制动性能的影响进行了研究;文献[ 6]提出了基于制动强度和车速的两参数主动降档辅助制动换档规律;文献[ 7]分析了车辆在下坡时的动力及阻力特性,提出了下坡工况利用发动机辅助制动力克服车辆加速的主动降档规律制定方法。
减速制动工况应在避免意外换档的前提下,结合驾驶意图和行驶环境,适时利用发动机进行辅助制动。意外换档消除策略可参考文献[ 8, 9, 10]。本文在分析发动机辅助制动的基础上,提出了基于模糊推理的、综合考虑驾驶员意图和行驶环境信息、利用发动机辅助制动的减速制动工况档位决策方法,并对该方法进行了道路试验验证。
自动变速车辆的换档策略通常以车速和油门开度作为控制参数,其在行驶环境复杂、驾驶员意图多变的情况下很难有令人满意的换档效果。在减速制动工况下,两参数换档策略如图1所示。
图1中的虚、实线分别代表5档降4档、4档降3档的换档策略曲线。假设驾驶员驾车以5档、40%的油门开度、80 km/h的速度行驶。在遇到特殊情况后,驾驶员松开油门踏板,然后开始制动。这一过程在图中由A、B、C、D四点表示。A点到B点代表驾驶员松开油门踏板的过程,在B点油门开度为0%。伴随着驾驶员的制动行为,车速开始下降。车速变化曲线分别与5档降4档、4档降3档曲线相交于C、D两点,即在C点发生首次降档、在D点发生第二次降档动作。由图1可知,在减速制动工况下,两参数换档控制策略退化为基于车速的单参数换档控制策略。无论制动强度大小,行驶环境如何(坡路或平路),驾驶员意图如何,降档点固定不变,始终是C点、D点。从乘车舒适性角度来说,减速制动工况下的换档点应能够随着驾驶员意图、行驶环境变化而改变;从行驶安全性角度来说,减速制动工况下应适时换档,以充分利用发动机辅助制动。
对于有经验的驾驶员,在减速制动工况下,遇到下长坡、泥泞、雨雪路面时,一般会挂低档利用发动机辅助制动,以提高制动稳定性,保证行车安全[ 11]。
发动机辅助制动是靠汽车传动机构,强迫发动机加速运转来产生阻力而实现牵阻作用的[ 11]。在发动机辅助制动情况下,发动机成为吸收能量的装置。车辆在正常行驶过程中,驾驶员放松油门踏板,此时若不切断车辆发动机与传动系的联系则产生发动机辅助制动效果。发动机辅助制动力矩可用如下的经验公式表示[ 12]:
T ne=T0+kn e(1)
式中:T ne为发动机辅助制动力矩;T0为与转速无关的常量;k为由发动机特性决定的系数;n e为发动机转速。
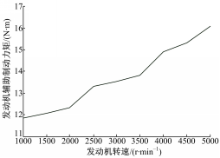
一般情况下,发动机辅助制动力矩与发动机转速的关系可通过平路滑行试验方式测得[ 5]。图2为依据该试验方法测得的试验车辆的发动机辅助制动力特性曲线。结合图2及式(1)可知:发动机辅助制动力矩随发动机转速的升高而增大。因此,为充分利用发动机辅助制动作用,应使发动机转速处于较高的水平。
发动机辅助制动力的等效制动强度可表示为[ 4]:
z e=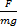 = = 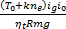 | (2) |
式中:z e为发动机辅助制动的等效制动强度;F为发动机作用在车轮上的辅助制动力;m为车辆质量;g为重力加速度;i g为当前档位传动比;i0为主减速器传动比;η t为传动效率;R为车轮半径。
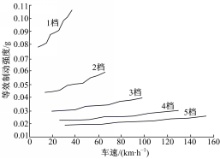
图3为依据式(2)计算得到的试验车辆各档位发动机辅助制动力矩的等效制动强度。由图3可知:在同样车速情况下,档位越低,发动机转速越高,则发动机辅助制动产生的车轮制动力越大,等效制动强度越大;同档位下,发动机转速(车速)越高,等效制动强度越大,制动效果越好。
综合上述分析可得减速制动工况下的发动机转速对应其发动机辅助制动力的情况。本文所研究的减速制动工况换档控制策略是通过降档来满足驾驶员在一定行驶环境下的辅助制动力需求的。
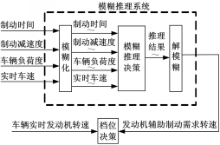
解决减速制动工况下两参数换档策略所存在的问题的关键是使换档策略适应驾驶员意图及行驶环境的变化。有经验的驾驶员在减速制动工况下会针对当前行驶环境、车辆状况,结合驾驶意图做出决策,采取相应的换档动作。驾驶员换档决策的依据是其对于发动机辅助制动力的需求,即当前档位下发动机产生的辅助制动力小于驾驶员需求辅助制动力时,进行降档。由于制动工况的复杂性,普通的决策手段难以达到良好的效果,而模糊推理方法能够模仿人的控制经验和策略[ 13],解决此类问题具有较好的鲁棒性,因此本文采用了该方法进行档位决策。基于模糊推理的减速制动工况档位决策系统结构如图4所示。
为了反映驾驶员意图和行驶环境信息,模糊推理系统的输入分别为制动时间、制动减速度、车辆负荷度及车速。减速制动工况下,制动减速度为:
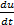
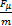
式中: du/ dt为制动减速度;F μ为制动器制动力;m为车辆质量。
驾驶员初始制动时,地面制动力F Xb等于制动器制动力F μ,且随制动踏板力F p增长成比例地增长。制动减速度的大小与驾驶员施加的制动踏板力有一定的关联。因此制动减速度及制动时间是减速制动工况下反映驾驶员意图的量。
车辆负荷度定义为[ 14]:
F load=F t-F f-F w-F j(4)
式中:F load为车辆负荷度;F t为零负载工况下的驱动力;F f为滚动阻力;F w为零负载工况下的空气阻力;F j为零负载工况下的加速阻力。为便于计算,一般使用其基于转矩的计算式。
车辆负荷度可以综合反映车辆行驶过程中的坡道、载荷、行驶阻力等信息。当下坡行驶时,负荷度为负值,模糊推理系统可据此识别下坡工况,保证减速制动工况下,车辆在下坡路段行驶时,更早降档以增强发动机辅助制动作用。驾驶员制动时的车速信息反映了制动时刻的车辆状况。车速高低对制动工况下的换档决策有不同程度的影响,车速较低时一般不考虑利用发动机辅助制动。因此模糊推理系统需参考该量。
模糊推理输出为发动机辅助制动需求转速。发动机辅助制动需求转速代表了当前驾驶员的辅助制动力需求程度。减速制动工况下换档动作实质是满足驾驶员对发动机辅助制动力的需求。档位决策过程为:
(1)当发动机当前转速大于此需求转速,则保持档位行驶。
(2)当发动机当前转速小于模糊推理输出需求转速时,则进行降档,以提供更大的发动机辅助制动力。
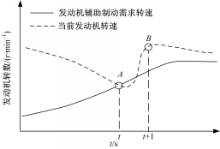
图5为档位决策过程示意图。由图5可知,随着制动的持续进行,车速(也即发动机转速)在逐渐下降;t时刻当前发动机转速(A点)等于发动机需求转速,而t时刻之后小于需求转速,因此执行降档动作;降档后在t+1时刻发动机转速升至B点,大于需求转速,保持档位行驶。
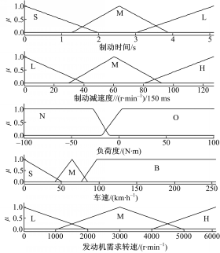
模糊推理系统的隶属度函数主要完成精确量的模糊化,即把物理量的精确值转换成语言变量值,以进行模糊推理决策。输入有制动时间、制动减速度及实时车速。其中制动时间Tmr_brk用{短(S),中(M),长(L)}描述,论域为[0,5];制动减速度 Ac_brk(单位为150 ms的变速箱输出轴速差)用{低(L),中(M),高(H)}描述,论域范围为[0,125];车辆负荷度Load_dif用{负(N),其他(O)}描述,论域范围为[-100,100];车速Sp_veh用{小(S),中(M),大(B)}描述,论域范围为[0,255];发动机需求转速Ne_brk用{低(L),中(M),高(H)}描述,论域范围为[0,6000]。针对上述各语言变量值的隶属度函数如图6所示。
模糊推理过程建立在一系列模糊规则的基础上。推理规则是人的推理经验的总结,推理规则可用条件语句描述,每条规则分别对应一种工况,例如:
if( Sp_veh==S) and( Ac_brk==L) and
( Load_dif==N) and( Tmr_brk==S) then
( Ne_brk=L)
该语句的含义为:如果车速小且制动减速度低且车辆负荷度为负且制动时间短,则发动机需求转速低。对应低速下坡时驾驶员减速制动工况,此时驾驶员需求的辅助制动力低。
模糊推理是应用模糊关系表示模糊条件句,将推理的判断过程转化为对隶属度的合成及演算过程。本文设计的模糊推理系统采用Mamdani算法。该算法的推理过程如下:
假设有模糊推理系统n条推理规则:
if A i and B i then C i( i=1,2,…, n)
式中:Ai、Bi、Ci、分别是不同论域X、Y、Z的模糊集合。当输入为x、y时,对应每条规则的推理结果 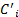
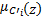 = = 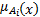 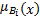 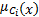 | (5) |
总的推理结果为:
μC'
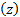 = = 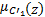 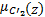 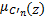 | (6) |
模糊判决是将模糊推理的结果解模糊的过程。针对上述推理结果,用重心法对其解模糊,采用如下公式:
z def=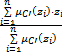 | (7) |
式中:z def为模糊判决结果;zi为论域Z中的相关元素。
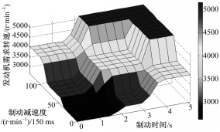
模糊推理系统利用推理算法依据推理规则将输入的制动时间、车辆负荷度、制动减速度及实时车速与输出的发动机需求转速建立了映射关系。通过MATLAB/Fuzzy ToolBox,可将输入量与输出量的关系用三维图形表示。
图7为车辆负荷度为-20 N·m、实时车速为85 km/h时,制动时间、制动减速度及发动机需求转速三者间的关系图。
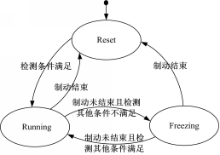
实时系统运行时,基于模糊推理的减速制动工况换档控制程序只在特定条件下被激活。这些条件包括:制动信号开启,发动机转速在合理范围内,车速在合理范围内及当前档位非最低档位。程序激活运行期间,这些条件被实时检测。当检测到的任一条件不满足,减速制动工况换档控制程序都会进入冻结状态。当驾驶员结束制动后,减速制动工况换档控制程序结束运行,这一过程如图8所示。
针对基于模糊推理的减速制动工况换档控制算法进行了基本功能试验及控制策略对比试验。试验车辆采用国内某AMT轿车硬件平台,TCU及其控制程序为自行开发,使用Vector CANape对道路试验中的实时数据进行采集。
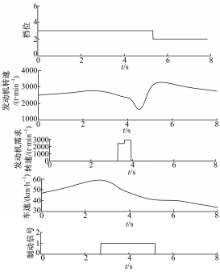
功能试验是验证减速制动工况换档程序是否达到初始设计功能的要求:即达到换档点随驾驶员意图及行驶环境而变化;充分利用发动机辅助制动作用。图9为水平路减速制动工况换档试验曲线。由图9可以看出,驾驶员在档位为3档,车速为53 km/h时制动。系统第1次计算出的发动机需求转速为2400 r/min,低于同一时刻发动机实时转速2595 r/min,可以满足驾驶员辅助制动力需求。第2次计算出的发动机需求转速为2880 r/min,高于同一时刻发动机实时转速2509 r/min,为了满足驾驶员对辅助制动力的需求,执行降档。降档时刻车速为47 km/h,远高于换档规律3档降2档车速17 km/h。实现了减速制动工况下换档点随驾驶员意图而改变的功能,充分利用了发动机辅助制动。
本文以同一路段、相同制动条件下,降低同等车速的时间作为对比指标。为了保证试验结果的准确及可信性,分别进行了水平路、下坡路状况下,有、无减速制动工况换档控制策略的多次试验。
试验时,驾驶员将车速保持在75 km/h一段时间(10 s左右),在此时间段内使车辆加速度维持在0左右。然后驾驶员快速松开油门踏板,以一定的制动强度开始持续制动。每次试验过程中,要保证驾驶员踩制动踏板产生相同的制动器制动力,需使制动期间驾驶员始终保持相同的制动踏板位置持续制动。为了避免驾驶员制动过程中的操作误差,对制动踏板进行了限位处理。当车速低于15 km/h时,驾驶员停止制动,一次试验结束。统计制动状态下,车速由70 km/h降至20 km/h的时间。由于每次试验中,驾驶员施加的制动力是恒定的,因此降速时间可以很好地反映出减速制动工况换档控制策略的效果。表1为对比试验的结果统计表。
从表1可以看出,平路试验及下坡路试验中,有减速制动工况换档控制策略的降速时间均小于传统两参数换档策略的降速时间。其中,有减速制动工况换档控制策略时,在水平路及下坡路的平均降速时间分别为8.45、12.61 s;传统两参数换档策略的平均降速时间分别为10.58、17.13 s。由此可见,减速制动工况换档控制策略较好地利用了发动机辅助制动。
| 表1 降速时间对比试验结果 Table 1 Comparison experimental results of decelerating duration s |
在减速制动工况的换档策略下,水平路及下坡路均降到了较低档位,在一定程度上保障了车辆行驶安全性。图10为水平路及下坡路有、无制动工况换档控制策略的对比试验曲线。
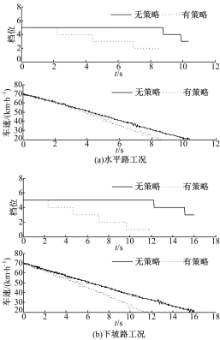 | 图10 有、无制动工况换档控制策略的对比试验曲线Fig.10 Comparison test curves between the gearshift strategy under braking conditions and the two-parameter strategy |
分析这几组曲线可以得出基于模糊推理的减速制动工况换档控制策略的优点:换档点随驾驶员意图及行驶环境变化而改变,辅助制动时的降档过程比无辅助制动时明显加快,相应地,降低到相同车速所用时间也缩短,克服了传统两参数换档策略在减速制动工况下的不足。
应用模糊推理理论解决自动变速车辆减速制动工况档位决策问题,避免了传统两参数换档策略的固有缺陷。该策略能适应驾驶员意图及行驶环境变化,充分利用了发动机辅助制动。道路试验结果表明:该策略具有较好的实用性,在一定程度上提高了自动变速车辆的行驶安全性。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|