引用本文
郑雪莲, 李显生, 任园园, 杨猛. 瞬时液体冲击对汽车罐车侧倾稳定性的影响. 2014, 44(3): 625-630
ZHENG Xue-lian, LI Xian-sheng, REN Yuan-yuan, YANG Meng. Rollover stability analysis of tank vehicle impacted by transient liquid sloshing. 吉林大学学报(工学版), 2014, 44(3): 625-630  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
瞬时液体冲击对汽车罐车侧倾稳定性的影响
郑雪莲1, 李显生1, 任园园1, 杨猛1,2
1.吉林大学 交通学院, 长春 130022
2. 黑龙江省交通科学研究所, 哈尔滨 150080
任园园(1982),女,讲师,博士.研究方向:车辆可靠性与安全技术.E-mail:maggie170101@gmail.com

郑雪莲(1987),女,博士研究生.研究方向:车辆可靠性与安全技术.E-mail:emma19870515@gmail.com

基金:国家自然科学基金项目(51375200,51208225);
摘要

为了探究准静态(Quasi-static,QS)方法对液体冲击的估计精度以及对汽车罐车准静态侧倾稳定性分析的准确性,分析了非满载椭圆柱罐体内瞬时液体冲击的实际值与QS方法估计值之间的关系。在此基础上,通过分析液体质心位移引起的车辆侧翻力矩和轮胎垂直载荷转移引起的回正力矩之间的平衡,研究了瞬时液体冲击对车辆侧倾稳定性的影响。并根据不同罐体车辆侧倾稳定性的分析结果,研究了影响液体冲击强度的关键因素和最优罐体形状。

关键词: 车辆工程; 汽车罐车; 准静态方法; 侧倾稳定性; 瞬时液体冲击; FLUENT仿真
中图分类号:U469.5 文献标志码:A 文章编号:1671-5497(2014)03-0625-06
Rollover stability analysis of tank vehicle impacted by transient liquid sloshing
ZHENG Xue-lian1, LI Xian-sheng1, REN Yuan-yuan1, YANG Meng1,2
1. College of Traffic, Jilin University,Changchun 130022,China
2. Communication Science Research Institute of Heilongjiang,Harbin 150080,China
Fund:
Abstract

To investigate the evaluating accuracy of Quasi-static (QS) method and the analysis correctness of tank vehicle rollover stability, the relationship between the actual transient liquid sloshing effects in partially-filled oval tanks and the QS evaluating results are studied. Then, the impact of transient liquid sloshing on vehicle rollover stability is investigated by analyzing the balance between the rollover moment caused by the movement of the center of gravity of liquid bulk and the aligning torque caused by the load transfer between tires of the two sides. Finally, the key points that influence the intensity of transient liquid sloshing and the optimal tank shapes are discussed based on the rollover stability analysis results of tank vehicles with different oval tanks.

Keyword: automobile engineering; tank vehicles; Quasi-static method; roll stability; transient liquid sloshing; FLUENT simulation

侧翻是汽车罐车交通事故中最主要的类型,约占事故总量的48.76%[ 1]。由于液体密度的不同和道路对轴荷的限制,汽车罐车多处于非满载状态。车辆运行状态的改变使得液体在惯性力作用下冲击罐体壁面,降低了车辆的稳定性。研究非满载罐体内的液体冲击是开展汽车罐车稳定性研究的关键。

目前,学者多采用试验/仿真方法、流体动力学法、等效机械模型法和准静态(Quasi-static,QS)方法研究非满载罐体内的液体冲击。其中,QS方法因具有简单便捷的特点得到广泛应用。在QS方法中,假定液体自由表面为一倾斜平面,通过计算不同加速度和充液比条件下的液体质心位置近似估计液体冲击对车辆稳定性的影响[ 2]。学者们使用QS方法研究了车辆上作用有加速度时液体质心的运动轨迹[ 3]、液体冲击对车辆侧倾稳定性的影响[ 2, 4]以及最优罐体形状的设计[ 5]。然而,关于QS方法对液体冲击计算精度的问题鲜有报道,仅有Modaressi在其研究中探讨了圆柱罐体内瞬时液体冲击的实际值与QS方法的估计值之间的关系[ 6],椭圆柱罐体作为常用罐体之一,并未在研究之列。因此,本文研究了非满载椭圆柱罐体内液体冲击的QS估计值与实际值之间的关系;在此基础上,通过分析液体质心位移造成的车辆侧翻力矩和回正力矩之间的平衡,探究了瞬时液体冲击对车辆侧倾稳定性的影响;并根据不同罐体车辆的侧翻稳定性情况,分析了影响液体冲击强度的关键因素,探求最合理的罐体形状。

1 瞬时液体冲击
1.1 QS方法

一阶冲击模态是罐体内液体冲击最重要的模态,其可用液体质心的位移描述。基于此,QS方法通过求解受侧向加速作用时液体质心的位移来近似估计液体冲击效果。

车辆上作用有侧向加速度时,液体在惯性力作用下运动,形成倾斜的自由表面。当侧向加速度不大于0.4 g时,液体自由表面近似为倾斜的平面,其斜率为:

tanφ=(ay+θ s)/(1-ayθ s) (1)

式中:φ为自由液面的倾斜角度;ay为车辆侧向加速度,9.8 (m·s-2);θ s为车身侧倾角。

任意外力条件下的液体质心位置可通过液体横断面关于两坐标轴的静矩和其面积的比值获得。

经证明,受外力作用时,非满载椭圆柱罐体内的液体质心运动轨迹为椭圆形,运动轨迹与罐体外周平行。经推导,椭圆柱罐体内的液体质心运动轨迹可表示为:

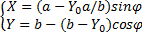(2)

式中:Y0为液面水平时液体质心的y轴坐标;a为罐体宽度的一半;b为罐体高度的一半。

QS方法中,液体对罐体壁面的冲击力可表示为:

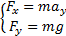(3)

式中:Fx为液体水平冲击力;Fy为液体垂直冲击力;m为罐体内的液体质量。

1.2 瞬时液体冲击的理论分析

实际中,受侧向加速度作用的液体自由表面是一个光滑的曲面,而非平面。忽略液体冲击沿罐体纵向的微小差异,认为任意纵向位置的液体横断面形状相同,即液体质心在罐体纵向的位置总是位于罐体的中点。根据有限差分法的思想将液体横断面分成足够多、面积足够小的单元,则液体质心的x轴和y轴坐标可表示为:

(4)

其中:x(t)、y(t)分别为瞬时液体质心的横向和纵向坐标;x c、y c分别为液体单元中心的横向和纵向坐标;A c为液体单元的面积。

与罐体壁面接触的液体单元产生作用在罐体上的压强,因而液体对罐体壁面的冲击力可表示为:

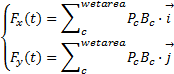(5)

式中:Fx(t)、Fy(t)分别为瞬时液体冲击对罐体壁面的水平和垂直冲击力;P c为与罐体壁面接触的液体单元作用于罐体壁面上的压强;B c为与罐体壁面接触的液体单元的面积。

液体冲击产生的绕罐体上某一点的力矩可表示为从受力点指向施力点的径矢与力矢的叉乘:

(t)=∑ (t)× (t) (6)

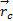
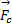
式中:r c(t)为由罐体上的受力点指向液体质心的径矢;F c(t)为瞬时液体冲击产生的冲击力。

1.3 瞬时液体冲击的FLUENT仿真

FLUENT通过有限差分法迭代求解一定初始和边界条件下的流体动力学基本方程。文中选择VOF模型处理气液两相流动问题。

调查发现:绝大部分汽车罐车的罐体横截面积在2.4 m2左右。以楚胜CSC5310GJYD加油车为例,其罐体外形尺寸为2.3 m×1.4 m,有效容积为24.8 m3。在罐体横截面积相同的条件下,令a/b的值从1变化至2,变化步长为0.25,以包含尽可能多的椭圆柱罐体。

充液比定义为水平液面至罐体底部的距离与罐体高度的比值。根据实际情况,文中设定罐体的充液比在0.4~0.8内变化,变化步长为0.1。令罐体侧向运动的加速度为0.1 g,对不同充装条件下的5种罐体进行瞬时液体冲击仿真。仿真过程中记录液体质心坐标以及水平和垂直冲击力。

1.4 仿真结果分析

5种罐体内的液体振荡角频率如图1所示。随着充液比的增加,液体冲击频率不断提高。相同充液比条件下,罐体的离心率越大,液体冲击频率越低。5种罐体内液体的最低冲击频率为2.6 Hz,该值远大于车辆方向盘转角的操纵角频率(0.2~0.8 Hz),可知车辆在行驶中不会发生共振现象。

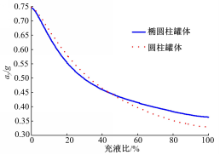
图1 液体冲击角频率Fig.1 Liquid sloshing frequencies

以a/b=1.5的罐体为例,记录一个振荡周期内冲击力和液体质心位移的最大值、最小值和平均值,同时利用式(1)~(3)计算相同条件下相应物理量的QS估计值,所得结果如图2所示。

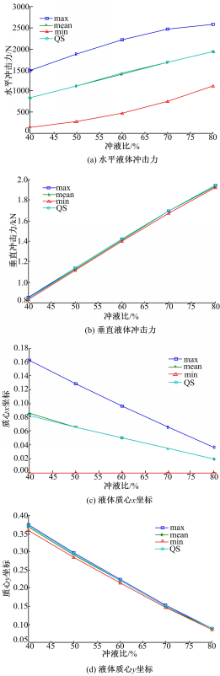图2 实际液体冲击效果与QS计算值比较Fig.2 Pracitice liquid sloshing effect and the cooresponding QS calculation results

非常明显地,瞬时液体冲击效果的平均值与相应物理量的QS计算值近似相等,二者比值为0.991~0.999;而且,一个振荡周期内瞬时液体冲击效果的平均值约等于其最大值和最小值之和的一半。4个物理量中, max(Fx(t))远大于Fx; max(x(t))远大于X;而 max(Fy(t))和Fy差别不大, max(y(t))和Y差别不大。由此可知:瞬时液体冲击的水平冲击力和质心x轴方向的位移是决定瞬时液体冲击对车辆侧倾稳定性影响的关键因素。对于其他形状罐体,所得结论与a/b=1.5的罐体相似,不再赘述。

令:

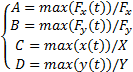(7)

式中:A、B、C、D代表瞬时液体冲击效果对比相应物理量QS计算值的放大率。

根据FLUENT仿真结果,得到侧向加速度为0.1 g、5种罐体的充液比从40%上升至80%时的放大率如表1所示。

表1 瞬时液体冲击效果的放大系数 Table 1 Amplification of transient liqiud sloshing parameters
2 瞬时冲击对侧倾稳定性的影响

本文从静态分析的角度探讨瞬时液体冲击对车辆侧倾稳定性的影响。车辆的侧倾稳定性取决于使车身产生侧倾的翻转力矩OM和防止车辆侧倾的回正力矩RM的平衡;而且,OM和RM都主要与整车簧上质量的质心位移有关。由簧上质量质心位移引起的翻转力矩记为OM c,由其他因素引起的翻转力矩记为OM r,且两值相比OM c较小;由左右轮胎垂直载荷转移引起的回正力矩记为RM c,由其他因素引起的回正力矩记为RM r,且两值相比RM c较小。

假设车辆悬架为线性系统,且轮胎与地面之间的摩擦力未超过轮胎与地面之间附着力的极限值,则有:

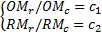(8)

式中:c1、c2为[0,1]之间的常数。

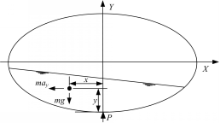
为了方便汽车罐车的侧倾稳定性分析,令簧上质量的侧倾中心位于罐体最低点P。根据图3即可列出液体质心绕点P的翻转力矩OM c和地面对轮胎的支反力造成的绕点P的回正力矩RM c。对于QS方法:

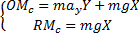(9)

图3 罐体侧倾分析图Fig.3 Tank roll analysis

当考虑瞬时液体冲击时(仅考虑瞬时液体冲击对车辆侧倾稳定性的最大影响程度):

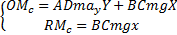(10)

根据车辆侧倾稳定性的判定条件,有:

OM c+OM r=RM c+RM r(11)

因而有:

(12)

因此,瞬时液体冲击造成的车辆侧倾稳定性的最大下降幅度即可表示为:

= -1 (13)

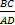
图4为用QS方法获得的圆柱和椭圆柱罐体( a/b=1.5)侧向加速度的侧翻极限值[ 5]。通过比较两种罐体车辆的侧倾稳定性下降幅度就可判断出实际情况下的车辆侧倾稳定性能的优劣,如图5所示。

图4 利用QS方法获得的车辆侧翻极限值Fig.4 Vehicle rollover threshold obtained by QS method

图5 瞬时液体冲击对车辆侧倾稳定性的影响Fig.5 Influence of transient liquid sloshing on vehicle roll stability

为了验证所得结果的正确性,通过整车动力学建模的方法求解了瞬时液体冲击对车辆侧倾稳定性的影响,获得5种罐体形状的汽车罐车侧翻加速度极限值,如图6所示。由图4~图6可知:采用静态分析法能简单快捷地获得瞬时液体冲击对车辆侧倾稳定性的影响程度。

图6 考虑瞬时液体冲击时的车辆侧翻极限值Fig.6 Vehicle rollover threshold considering transient liquid sloshing

图5表明:瞬时液体冲击对汽车罐车的侧倾稳定性有很大影响。相比QS计算结果,瞬时液体冲击使车辆的侧倾稳定性下降105%以上。罐体的离心率越小,车辆侧倾稳定性下降程度越大;而随着充液比的提高,所有罐体车辆的侧倾稳定性下降程度均呈增大趋势。

3 瞬时液体冲击的关键影响因素

由式(12)和表1可知:瞬时液体水平冲击力和质心x轴方向位移是造成汽车罐车侧倾稳定性下降的主要原因。

非满载罐体内的液体冲击强度与液体自由冲击空间的大小和空间形状有关[ 7]。对于本文的研究对象,在充液比相同的情况下,各个罐体内的液体自由冲击空间大小是相同的。因此,仅讨论空间形状对液体冲击强度的影响。

液体自由冲击空间形状可由水平液面至罐体顶部的距离h、水平液面的长度l和水平液面与罐体壁面的夹角θ三个参数描述。

h=2b(1-Δ) (14)

l=2a(15)

θ= arctan( 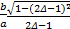) (16)

式中:Δ为充液比。

表2为充液比为40%和60%时,5种罐体的h,l和θ的值。

表2 不同充液比条件下 h, l和 θ的值 Table 2 The values of h, l and θ as a function of fill level

由表2可知:相同充液比条件下,水平液面至罐体顶部的距离越小、水平液面长度越大、罐体形状的曲率变化越大,瞬时液体冲击对车辆侧倾稳定性的影响就越小。三个参数中,距离h和长度l的影响较大。因此,在满足罐体尺寸公路运输限制的前提下,方形横截面罐体是保证车辆拥有良好侧倾稳定性的最优罐体形状。

4 结束语

非满载罐体内液体冲击效果的QS估计值与一个振荡周期内瞬时液体冲击效果的平均值近似相等,说明QS方法能够准确地预测随充液比的增加汽车罐车侧倾稳定性的变化趋势;然而,由于瞬时液体水平冲击力和质心x轴位移的最大值远大于相应物理量的QS估计值,通过QS方法获得的车辆侧倾稳定性结果较为保守,实际车辆的侧倾稳定性要远低于QS方法的计算结果,下降幅度在105%以上。通过不同椭圆柱罐体的液体自由冲击空间形状的对比,得出方形横截面罐体是保证车辆拥有良好侧倾稳定性的最优罐体。

The authors have declared that no competing interests exist.

参考文献
[1] 刘凯峥, 刘浩学, 晏远春, 等. 罐体车辆道路运输危险品事故特征分析[J]. 安全与环境学报, 2010, 10(3): 130-133.
Liu Kai-zheng, Liu Hao-xue, Yan Yuan-chun, et al. Analysis of the road accidents with tank-vehicle transportation of hazardous materials[J]. Journal of Safety and Environment, 2010, 10(3): 130-133. [本文引用:1] [CJCR: 0.6347]
[2] Ranganathan R, Rakheja S, Sankar S. Steady turning stability of partially filled tank vehicles with arbitrary tank geometry[J]. Journal of Dynamic Systems, Measurement, and Control, 1993, 111(3): 481-489. [本文引用:2] [JCR: 0.758]
[3] Southcombe E, Kuznetsov E, Ruhl R L. Fluid load analysis within the static roll model[C]∥SAE Technical Paper, 2000-01-3476. [本文引用:1]
[4] 李显生, 郑雪莲, 刘宏飞. 非满载罐式半挂汽车列车侧倾稳定性评价改进算法[J]. 吉林大学学报: 工学版, 2012, 42(5): 1089-1094.
Li Xian-sheng, Zheng Xue-lian, Liu Hong-fei. Improved algorithm on roll stability evaluation of partially filled tractor-tank semitrailer[J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(5): 1089-1094. [本文引用:1] [CJCR: 0.701]
[5] Kang X, Rakheja S, Stiharu I. Optimal tank geometry to enhance static roll stability of partially filled tank vehicles[C]∥SAE Paper, 1999-01-3730. [本文引用:2]
[6] Modaressi-Tehrani K, Rakheja S, Sedaghati R. Analysis of the overturning moment caused by transient liquid slosh inside a partly filled moving tank[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2006, 220(3): 289-301. [本文引用:1] [JCR: 0.583]
[7] Romero J A, Ranirez O, Fortanell J M, et al. Analysis of lateral sloshing forces within road containers with high fill levels[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2006, 220(3): 303-312. [本文引用:1] [JCR: 0.583]