于尧(1985),男,博士研究生.研究方向:城市智能交通,交通控制与诱导.E-mail:yuyao11@jlu.edu.cn
针对现有路径诱导算法无法实现多点连续搜索的不足,提出了一种可以满足出行者一次出行中访问多个兴趣点(Point of interest, POI)的ASSA算法(A*-based sequenced search algorithm)。ASSA算法优化了路网搜索结构,大幅地减少了数据访问量,并通过兴趣点近邻区域的时空关联推理,得到最优出行路径。并基于城市POI兴趣点信息,对兴趣点数据进行了分类划分,设计了多规则下的兴趣点访问机制,并对其进行了试验验证。结果表明:相比于NS最近邻算法,提出的ASSA算法可以提高计算性能16%以上,并避免了非最优路径的出现,可以有效地满足出行者不同规则下的兴趣点访问需求。
To overcome the shortcoming that the existing route guidance algorithms can not execute sequenced route search, a new Artificial Searching Swarm Algorithm (ASSA) is developed that can query multi-Point of Interests (POIs) in travel processing. The ASSA can optimize search topological structure of the road-network, which greatly reduces the amount of data access. Thus the optimal path can be presented according to the spatial-time correlation reasoning. Further more, the POI data are categorized based on urban POIs and a method to go through the sequenced POIs under multi-rules is developed. Sensitive experiments were implemented to verify the proposed ASSA. Results show that, compared with NS algorithm, ASSA can improve the computing efficiency by at least 16%, and it can also avoid getting less-than-optimal path. It effectively meets the travelers' sequenced travel demand.
随着GIS地理信息的不断完善,路径导航[ 1, 2]得到了人们越来越多的关注及应用。兴趣点信息的完善极大地方便了人们的出行,在出行前即可规划好去目的地的最短路径[ 3, 4]。以一次出行为例,出行者通常需要先到餐馆、银行、商场等多个地点,最后抵达目的地。然而现有诱导算法大都以单兴趣点为诱导目标,忽略了实际出行中出行者的中途停留需求,无法实现多个兴趣点的连续路径规划。
近年来,一些学者针对连续行程规划问题[ 5](STPQ)提出了相关的近似查询算法,如Sharifzadeh等[ 6]提出的最优有序路径算法(OSR-LORD)、Lee等提出的NS最近邻算法[ 7]、Terrovitis等[ 8]提出的a自治最短路径规划和k停顿最短路径规划方法等,这些算法(方法)实质上都可以看成是多兴趣点连续路径规划的特例问题,不具有一般性。Chen等在文献[9]中阐述了多类别兴趣点有序路径查询问题,通过约束兴趣点访问顺序,得到不同约束规则下的路径查询效果,但其查询的兴趣点数据必须与其内部的数据集构成有拓扑关系,且提出的算法仅为数据查询机制,未能与实际路网地图匹配。所以如何有效、快速地响应用户对多兴趣点的访问请求,是实现高效路径引导服务的基础,也是未来几年内路径诱导领域的研究兴趣点。本文依据城市兴趣点认知程度,对其进行分类,并基于不同出行规则约束,提出了最近邻连续兴趣点搜索方法,旨在满足多出行规则约束下的访问需求,丰富了现有路径诱导方法。
城市兴趣点(Point of interest,POI)包括餐饮、购物、旅游以及汽车服务等多种类别。这些兴趣点信息已在地理信息服务中得到了广泛的应用[ 10, 11]。POI信息不但可以帮助用户快速定位所需位置信息,还可以在导航中利用一定的规则进行推理,得到实时位置关联度最高的一系列地标[ 12],进而实现简洁、灵活和高效的路径引导服务。
Raubal等[ 13]提出,城市中的任何要素,只要人们对它的认知度较高,即可以被看做是熟知的地点。本文将人们日常出行过程中需要经常访问的地点定为POI,并参照文献[12],定义各类POI的基本选取范畴,如表1所示。
定义表1中的12种兴趣点分类为 

| 表1 POI分类 Table 1 POI classification |
实际上最近邻兴趣点路径搜索与数据库中的对象修剪与精炼过程类似[ 14]。但不同于旅行商问题(TSP)[ 5, 15],算法并不需要遍历每一个地图上已有的兴趣点,而是仅仅计算用户事先给定所需访问的兴趣点类别即可。
假设小A现有一个出行计划,她想到达车站之前,先去银行取钱,再分别至商场、加油站以及餐馆等4个地点,那么小A的出行路径有以下两种:①出发点→银行→餐馆→商场→加油站→车站。②出发点→银行→商场→餐馆→加油站→车站,如图1所示。
出行用户可以自己定制访问的兴趣点规则,如餐馆→商场,或者商场→餐馆,这时两种不同路径下出行时间的长短将成为辅助出行者决策的重要依据。
对于出行起点周边的最近邻兴趣点信息搜索(Nearest POI Search,NPS),做如下规定,如图2所示,图中的黑色点q代表用户的出行位置,空心点A、B、C、D、E、F代表路网节点(如交叉口),三角形P1、P2、P3代表路网中的兴趣点信息,数字代表路段的权重(本文中选择距离为权重系数)。
搜索当前离q最近兴趣点位置的步骤为:首先选取与q点相连接的路网节点(C、D),并初始化队列Q=<(C,5),(D,7)>;判断CD中是否有P存在,若无,紧邻q点的节点C出队,节点A、E进队列Q中,Q更新为Q=<(D,7),(A,9),(E,10)>由于CA、CE段上没有P存在,故同节点C一样,节点D出队,紧邻D点的B、F进队,更新Q,Q=<(A,9),(E,10)(F,10),(B,15)>接下来在BD段上搜索到P3,计算q至P3的距离为9,判断目前Q中其余节点至q点的距离可知,没有小于9的路径,所以搜索完成,q点至最近兴趣点P3的最短距离即为9。
在最近邻兴趣点路径搜索规则的基础上,提出基于A*的连续搜索算法(A*-based sequenced search algorithm,ASSA),算法考虑了用户设置的终点信息,通过分别计算起点与终点至兴趣点P的最短距离(如式(1)所示),得到总出行费用(距离)最小的路径,避免了非最短路径的出现[ 16],如图3所示。
LOD= Mini,j∈(1,n){ Dist(S,Pi)+ Dist(Pi,Pj)+…+ Dist(Pj,D)} (1)
图3中的虚线代表未考虑出行终点D时的出行路径,实线为考虑D点后的出行路径。可以看出,未考虑D情况下的出行距离要远大于后者。
采取与经典启发式算法类似的估价方法,设(s,d)为ASSA算法选定的包含兴趣点pi至兴趣点pj间的行驶路线,令f(l)=ω(s,pi)+c(pi,d),其中ω(s,pi)为从起始点s到达兴趣点pi的权值之和,c(pi,d)为兴趣点pi的代价函数,它预测了从pi到目的地d的代价。f(l)的值决定了该兴趣点是否能够被优先查找。
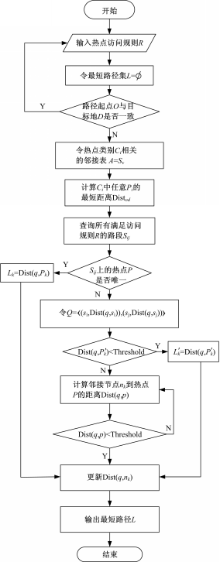
为了减少路网搜索范围,通过出发点O、目的地D以及OD间的欧式距离确定一个椭圆,这个椭圆的焦点即为O、D,这样可以有效减少算法的搜索范围。采用不同形式的数据存储形式,会对算法的执行效能产生较大影响。在路网规模较大时,应采用表形式存储数据,此时遍历效率远高于邻接矩阵的存储形式[ 17]。在本文中,采用与Dijkstra相似的表形式用以存储路网及兴趣点数据,即初始搜索点将被添加至Sv表中,而L最短路径表为空表状态。设兴趣点访问规则为R,那么算法的时间复杂度即为R2。其算法流程图如图4所示。
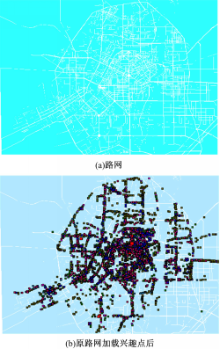
试验平台配置如下:2.8 GHz双核处理器,2 GB内存,操作系统为WindowsXP。试验路网选择长春市实际路网,共包括3421个结点以及5771个路段,如图5所示。其中结点的存储形式为{Node_ID,Longtitude,Latitude},路段的存储形式为{Edge_ID,Strat_Node_ID,End_Node_ID}。出行起始点采用随机数发生器产生的服从均匀分布的点数据。采用Mapinfo7.0+Mapx以及Visual C++6.0对所提算法进行编程实现。
路网中共含有12个兴趣点图层,本文仅取宾馆酒店、大厦、车辆服务、银行、商场、政府、学校以及休闲场所共计8个兴趣点分类中的主要兴趣点,各兴趣点数目如表2所示。通过对比文献[7]中提到的全方位最近邻算法(NS),分别在计算时间和搜索距离两方面分析了不同出行约束条件下两种算法的表现。NS算法[ 7]是数据遍历算法中较为成熟、广泛使用的一种数据关联搜索算法,具有较高的实用性。为了不失一般性,出行规则选择在银行和大厦,商场和车辆服务(如加油站)等不同兴趣点类别之间随机发生。
| 表2 不同兴趣点类别包含的兴趣点数 Table 2 Number of POIs in different categorization |
当出行规则一定时,相比于NS全方位搜索算法,ASSA算法的计算时间明显要优于NS算法,如图6所示。随着兴趣点基数的增加,两种算法的计算时间都有显著增加,以NS算法为例,当兴趣点数为3500个时,算法的计算时间相比500个兴趣点时增加了3倍以上;当出行约束条件增加时,也就是说用户定义的访问规则占全部需访问兴趣点类别的比例增加时,可知虽然NS算法和ASSA算法的计算时间都呈现线性增加,但计算时间要低于 R/C=0.333时的情景,这是因为,约束规则增加,算法所需遍历搜索的数据空间就随之减少,所以算法的执行时间也相应变短。
 | 图6 不同约束条件下ASSA算法与NS算法的计算时间对比Fig.6 Computed time comparison between ASSA and NS under two different constrained conditions |
由图7可知,用户选择兴趣点数目的多少直接影响着ASSA算法的计算时间和路径搜索距离。随着兴趣点访问类别的增加,可知用户的出行距离也要相应增加,由于算法需要响应这一系列的出行规则,所以其路径搜索距离以及计算时间两项指标都有明显的上升,但ASSA的计算时间仅为0.191 s。相比NS算法,ASSA算法的执行效率要优于其16%以上。
以城市兴趣点信息为基础,提出了基于A*的连续搜索算法(ASSA),该算法能够快速地响应用户的多兴趣点访问要求,并提供最短行驶路径。通过试验可知,提出的ASSA算法在运行效果上要明显优于NS全方位最近邻算法,并可避免非最短路径的出现。但由于面向多兴趣点信息的位置服务理念提出的较晚,因此对这类算法的研究依然处于起步阶段,考虑的因素还不够全面,实时性等有待进一步提高。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|