杨爱武(1971),男,教授,博士.研究方向:软土地基处理及土体微观结构.E-mail:tulilab@163.com
对CJDS07型固化剂固化的天津滨海吹填软土的力学特性试验研究。结果表明:吹填固化土的压缩模量、抗剪强度、结构性都随着龄期的增长逐渐增加,固化土逐渐由高压缩性转化成为中压缩性。吹填固化土的应力-应变关系受围压的影响较大,当围压小于某一值时,应力-应变曲线为应变软化型,反之为应变硬化型。基于以上研究成果,以邓肯张模型为基础,建立了适用于吹填固化土的应力-应变关系模型。
The mechanical characteristic of the soft dredger fill, which is stabilized by the CJDS07 agent, is studied in Tianjin new area. The results show that the compression modulus, shear strength and structure of the stabilized soft dredger fill increase with the curing age. The stabilized soil gradually changes from high compressibility to middle compressibility. The stress and strain relationship of the stabilized soil is highly influenced by the confining pressure, that when the confining pressure is smaller than a certain value, the relationship is tend to be strain softening, otherwise, it is strain hardening. Based on the above research results and Dun-Chang model, the stress-strain relationship model suitable for the stabilized dredger fill is established.
随着天津滨海新区的大规模开发,吹填造陆已成为新区开发土地资源的主要途径,与之相关的理论及技术方法引起了学术界和工程界的广泛关注[ 1]。天津滨海新区吹填软土以细粒为主,具有含水量高、孔隙比大、压缩性高以及固结性能差和低承载力等特征,很难直接满足工程需求,利用土壤固化剂固化吹填土,能使吹填土尽快地从淤泥状态转变成为具有一定承载力的地基。目前,人们主要从固化土的强度特性[ 2, 3, 4]、压缩变形特性[ 5, 6, 7]及本构关系[ 8, 9]等几个方面对固化土的力学特性进行研究和探讨。本文利用自行研制的CJDS07型固化剂对天津滨海新区的吹填软土进行固化,对固化土的压缩特性及抗剪强度特性进行了分析,并建立了固化土应力-应变关系模型。
土样取自天津滨海新区临港工业区吹填现场,为未经处理的高含水量吹填软土——淤泥质粘土,土样基本物理性质指标为:比重 Gs=2.76;水质量分数 w(H2O)=86.8%;液限 WL=42.4%;塑限 Wp=21.4%;塑性指数 Ip=21.0;液性指数 IL=3.11。所用固化剂为自行研制的CJDS07型固化剂,主要由主剂32.5的矿渣硅酸盐水泥和外加剂熟石膏粉、工业分析纯NaOH及Na2CO3按一定比例配制而成。
试验模具面积为30 cm2的环刀和三瓣模(直径39.1 mm,高80 mm),按试验方案将固化剂加入相应的土样中,人工分层捣制成型。试样制备完成后,自然养护1 d脱模,并称重。将试样装入撒水湿润后的塑料保鲜袋中,置于标准养护室内进行养护,养护温度控制在(25±2) ℃,相对湿度≥95%,养护至所需龄期。试样在测试前一天均浸水24 h,水面高出试样约2.5 cm,到测试时间取出试样,先用软湿布吸去试样表面的可见自由水,然后进行试验。
本文压缩回弹试验在轴承式单杠杆固结仪上进行,分别对养护龄期为7、14和28 d的固化土进行压缩与回弹试验,其中压缩试验加载方式:7 d和14 d为25 kPa→50 kPa→75 kPa→100 kPa→150 kPa→200 kPa→300 kPa→400 kPa→600 kPa→800 kPa;28 d为50 kPa→100 kPa→200 kPa→300 kPa→400 kPa→600 kPa→800 kPa→1000 kPa→1200 kPa,回弹方式如表1所示。在水质量分数分别为60%、70%和80%三种吹填软土中加入CJDS07型固化剂,将加入固化剂后的土制成环刀样,将不同含水量,不同龄期的固化土制作环刀样,并选取3种卸载方式(分别编号为1,2,3),每个试样进行3组平行试样对比;三轴固结不排水剪切试验在应变控制式SJ-1A.G三轴剪力仪上进行,加荷速率为0.073 mm/min,对水质量分数为70%的固化土,7、14和28 d龄期的试样进行三轴固结不排水剪切试验,试验中不同龄期试样围压取值如表2所示。
| 表1 固化土不同龄期试样的回弹试验方案 Table 1 Rebound test scheme of the solidified soil with different age |
| 表2 固化土不同龄期试样的固结围压 Table 2 Confining pressure of solidified soil with different age |
表3~表5为不同含水量的各龄期固化土压缩及回弹试验结果,表中e0为原状土的初始孔隙比;a1-2为固结围压是100~200 kPa时的压缩系数。从表中可以得到以下结论:
(1)各龄期固化土孔隙比都很大,最高的达1.95,随着龄期的增长,各固化土孔隙比都随之减小,水质量分数分别为60%、70%、80%的吹填土固化后,固化土28 d孔隙比与7 d相比分别减少了16.4%、14.5%、13.4%,说明随着龄期的增长,固化土中不断有固体物质生成,这些物质填充了土中的部分孔隙,固化土逐渐变得密实。相同龄期下含水量高的土固化后孔隙比大。
(2)随着龄期的增长,各固化土压缩系数逐渐减小,压缩模量逐渐增大,龄期为7 d时,各固化土压缩系数都大于0.5 MPa-1,压缩模量都小于4 MPa,均为高压缩性土;当固化土龄期为28 d时,各固化土压缩系数都小于0.5 MPa-1,压缩模量都大于4 MPa。这说明随着固化土龄期的增长,固化土的压缩性逐渐减小,由高压缩性土转化成为中压缩性土,压缩模量提高了2~3倍,土的工程性质得到很大的改善。相同龄期下水质量分数高的土固化后压缩模量较小。
(3)随着龄期的增长,固化土回弹系数逐渐减小,回弹模量逐渐增大,同一固化土随卸荷比和卸荷时的压力不同而发生变化。当固化龄期为7 d和14 d,2号试样的回弹模量为1号试样的1.5倍左右,而3号试样的回弹模量比2号试样的回弹模量要小,比1号试样大;当固化龄期为28 d时,2号试样的回弹模量为1号试样的2倍左右,而3号试样的回弹模量为2号试样的1.5倍左右,也就是说在卸荷比相同时,固化土的回弹模量随卸荷时的压力增大而增大。对于同一种固化土,卸荷比相同时,回弹系数随卸荷时的压力增大而减小。卸荷比增大时,回弹系数的变化与固化龄期有关。当固化龄期为7 d和14 d时,回弹系数随卸荷比增大而增大,当固化龄期为28 d时,回弹系数随卸荷比增大反而减小。
| 表3 水质量分数为60%的吹填土固化后压缩及回弹试验结果 Table 3 Compression and rebound test results of soft dredger fill with water content of 60% solidified |
| 表4 水质量分数为70%的吹填土固化后压缩及回弹试验结果 Table 4 Compression and rebound test results of soft dredger fill with water content of 70% solidified |
| 表5 水质量分数为80%的吹填土固化后压缩及回弹试验结果 Table 5 Compression and rebound test results of soft dredger fill with water content of 80% solidified |
2.2.1 固化土三轴应力-应变关系
由图1所示的固化土应力-应变关系。
可以看出:各龄期的固化土应力应变曲线都呈现出两种形态:在低围压下曲线存在峰值点,达到峰值点后,应力随应变的增大反而变小,最终趋于平稳,即表现为应变软化型;而在高围压下曲线不存在峰值点,应力随应变的增大而增大,即表现为应变硬化型。
2.2.2 固化土莫尔破坏线
根据固化土在不同龄期和不同围压下的应力应变曲线,绘制出了固化土的强度包线如图2所示,图中圆圈表示的位置为结构屈服应力点,其对应的横坐标为固结结构屈服应力(或称临界围压),纵坐标对应为剪切结构屈服应力。
从图2可以看出:固化土的强度包线不再是过原点的一条直线,而是由两条直线拟合而成,交点处为结构屈服应力点。当外力小于固结结构屈服应力时,固化土的胶结结构基本未被破坏,结构损伤较小,此阶段对应的强度包线比较平缓,与纵坐标截距较大,即粘聚力c较大,固化土颗粒间的胶结作用较强;当外力大于固结结构屈服应力时,固化土的胶结结构出现大量的破损,结构损伤较大,结构被压密,此时固化土颗粒间的摩擦作用逐渐得到了发挥,表现出来的φ值较大。转折点前后两段强度包线的c、φ值如表6所示,从表中还可以看出:随着固化龄期的增长,固化土在结构屈服应力前后c、φ值都随之增大,抗剪强度得到了提高。
| 表6 不同龄期下固化土的强度参数 Table 6 Strength parameters of stabilized soil with different age |
邓肯-张模型[ 10]是被广泛地应用于工程实践中的本构模型。但邓肯-张模型仅适合于描述应变硬化型曲线,而本文的固化土应力-应变关系曲线在小围压下表现为应变软化型,若采用该模型势必会造成较大的误差。此外,该模型本质上体现为土体的线刚度软化特性,而本文固化土表现的是非线性刚度软化特性。基于以上分析,本文通过利用固化土的力学性质研究成果,结合固化土的非线性刚度软化规律,以邓肯-张模型为基础,试图建立一种能考虑应变软化的应力-应变关系模型。
邓肯-张模型[ 10]可表示为:
(σ1- σ3)=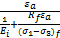 | (1) |
式中:ε a为轴向应变;(σ1- σ3)为偏应力;(σ1- σ3) f为破坏时的偏应力;R f为破坏比,E i为初始切线模量,其数值上等于初始割线模量E0。
静三轴试验中常采用割线变形模量E的大小来描述软土的刚度,E定义为应力-应变曲线上某点与原点之间的连线所得直线的斜率,即E=q/ε a,式(1)可以重新表示为:
 =1-R f =1-R f  | (2) |
式中: qmax为峰值偏应力; q为偏应力。
由式(2)可以发现,邓肯-张模型中反映的 q/qmax- E/E0关系为线性关系,随着无纲量偏应力 q/qmax(在此称之为应力水平)的增大,无纲量化割线变形模量 E/E0(在此称之为刚度比)线性减小,而固化土与超固结粘土类似,其 q/qmax- E/E0关系为非线性关系, 图3和图4为固化土7 d时的刚度比-应力水平关系曲线。
 | 图3 应变软化时固化土的刚度比-应力水平关系曲线Fig.3 Relationship between rigidity ratio and strain level of Stabilized soil with stain softening |
 | 图4 应变硬化时固化土的刚度比-应力水平关系曲线Fig.4 Relationship between rigidity ratio and strain level of Stabilized soil with stain hardening |
由图3可以看出:当围压小于临界围压时,固化土刚度比-应力水平曲线由两段组成。第1段为应力达到峰值之前,此阶段随着应力水平的增加,固化土刚度比逐渐减小,且此时两者的关系为非线性关系,刚度比减小速度先慢后快,这是因为在应力达到固化土剪切结构屈服应力前,固化土主要以弹性变形为主,应力随应变的增大基本呈线性增大,刚度衰减缓慢,当应力大于固化土的剪切结构屈服应力时,固化土开始以塑性变形为主,应力随应变的增大基本呈非线性增加,刚度衰减较快;第2段为应力达到峰值之后,此段应力水平与刚度比同时减小,曲线发生转型,即开始发生软化现象,此时两者的关系也为非线性关系,刚度比减速度先快后慢,这是因为在软化前期,应力随应变减小的速度较快,刚度随之衰减较快,而在软化后期,应力随应变减小的速度放缓,刚度随之衰减放缓。总体来看,随着围压的增大,曲线的转折点逐渐下降,对应的刚度比逐渐减小,当围压达到固结结构屈服应力后,将退化成如图4所示的曲线,固化土应力-应变关系将由应变软化型变为应变硬化型。
图4为围压大于固结结构屈服应力时的固化土刚度比-应力水平曲线,从图中可以看出:随着应力水平的增大固化土刚度比随之减小,刚度比减小速度也呈现出先慢后快的趋势,但总体相对比较平缓。
通过以上分析,本文拟在邓肯-张模型的基础上,对刚度比-应力水平呈非单调函数(见图3)关系的曲线,以拐弯点为界限分段进行描述。
第1段曲线部分采用:
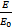 =1-a =1-a 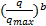 | (3) |
式中:a决定峰值应力时的刚度比;b决定刚度的衰减速度。
第2段的曲线部分采用:
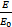 = = 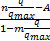 | (4) |
式中:m、n、A均为试验参数,其值的大小决定了应力-应变软化段的形状。
当刚度比-应力水平呈单调函数关系曲线(见图4)时,参照邓肯-张模型对其进行如下描述:
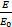 =1-λ =1-λ  | (5) |
式中:λ决定了破坏时的刚度比。
对上述模型中的参数,本文采用OriginLab软件[ 11]编辑公式对相关函数进行拟合,结果如表7所示。
| 表7 不同围压下固化土的模型参数 Table 7 Model parameters of stabilized soil with different confining pressures |
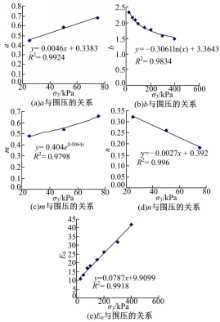
表7中的参数均与围压有关,其中A值基本为一常数,而λ随着围压的增大而减小,但变化不大,可近似为常数,A取平均值为0.092,λ取平均值为0.877,其他参数均为围压的函数,如图5所示。
由图5可知,参数a、n及E0均与围压呈近似线性关系,而参数b与围压的对数函数存在很好的相关性,m与围压的对数函数存在很好的相关性,且相关系数均在0.97以上。
根据莫尔-库伦强度准则有:
q max=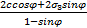 | (6) |
式中: qmax分两段计算,其分段所用的c、φ值如表6所示。
从式(6)中可以看出:当c、φ一定时, qmax与 σ3为线性关系,如图6所示。
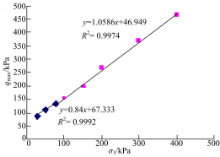 | 图6 固化土最大偏应力与围压的关系曲线Fig.6 Relationship between maximum deviator stress and confining pressure of solidified soil |
由图6可看出: qmax与 σ3的关系并非是完全的线性关系,而为两段直线,两直线的交点为结构屈服应力点,通过计算得对应围压 σm=93.1 kPa。当围压小于该值时,固化土的应力-应变曲线表现为应变软化型,计算 qmax时采用 c1、 φ1,当围压大于该值时,固化土应力-应变曲线表现为应变硬化型,计算 qmax时采用 c2、 φ2。
上述模型中共有8个参数:a、b、m、n、A、λ、E0和 qmax,各参数均与围压有关,易于确定。
将参数代入到模型中进行计算,得到应变软化与应变硬化两种情况下不同围压下的计算值,与实测值对比结果如图7和图8所示。
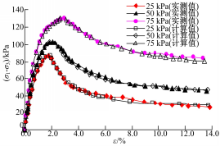 | 图7 应变软化时不同围压下固化土的计算值和实测值Fig.7 Calculation value and measured value of stabilized with strain softening under different confining pressures |
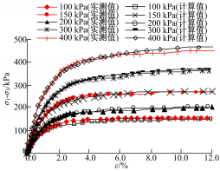 | 图8 应变硬化时不同围压下固化土的计算值和实测值Fig.8 Calculation value and measured value of stabilized with strain hardening under different confining pressures |
从图8中可以看出:模型计算值与实测值很接近,初步说明本文建立的模型能够描述天津滨海新区吹填固化土的应力-应变关系。
(1)随着龄期的增长,吹填固化土压缩系数逐渐减小,压缩模量逐渐增大,由高压缩性土转化成为中压缩性土,压缩模量提高了3~4倍,土的工程性质得到很大的改善。吹填固化土回弹系数随龄期的增长逐渐减小,回弹模量逐渐增大,且其随卸荷时的压力增加而增加。
(2)围压对吹填固化土的应力-应变关系有很大的影响,当围压小于某一值时,曲线保持为应变软化型,反之,曲线将转化为应变硬化型。吹填固化土的强度包线不再是过原点的一条直线,而是由两条直线组成的折线,即吹填固化土是一种结构性土,随着龄期的增长折线凹凸性越来越明显,结构性越来越强。随着固化龄期的增长,吹填固化土抗剪强度指标c、φ值都随之增大,抗剪强度得到了提高。
(3)通过对试验所得的固化土非线性刚度软化规律进行分析,在邓肯-张模型的基础上对天津滨海吹填固化土的应力-应变关系进行了合理的描述,初步建立了能够考虑应变软化的非线性本构方程,该方程独立参数少、易于确定。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|