引用本文
马文星, 胡晶, 褚亚旭, 王松林, 吴岳诗. 双涡轮液力变矩器超越离合器动载强度分析. 2014, 44(3): 675-679
MA Wen-xing, HU Jing, CHU Ya-xu, WANG Song-lin, WU Yue-shi. Dynamic load strength analysis of over-running clutch of dual turbine torque. 吉林大学学报(工学版), 2014, 44(3): 675-679  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
双涡轮液力变矩器超越离合器动载强度分析
马文星1, 胡晶1, 褚亚旭2, 王松林1, 吴岳诗1
1.吉林大学 机械科学与工程学院,长春 130022
2.北华大学 交通建筑工程学院,吉林 吉林132021
褚亚旭(1964),男,教授,博士.研究方向:机械设计及液力传动.E-mail:cyx.1964@sina.com

马文星(1962),男,教授,博士生导师.研究方向:液力传动与自动变速.E-mail:mawx@jlu.edu.cn

基金:吉林省科技发展基金项目(20080538);
摘要

首先,根据装载机一个工作循环内十二个工况下所对应的发动机转速和变矩器的转速比,计算出双涡轮液力变矩器每个状态下所对应的Ⅰ涡和Ⅱ涡的转速。其次,依据转速在CFD中计算出不同时间内Ⅰ涡和Ⅱ涡的转矩,从而计算出不同时间内超越离合器滚柱与内、外圈的受力值。再次,采用有限元方法对超越离合器进行动态分析,得出内、外圈与滚柱的瞬时应力分布图。最后,给出产生最大应力的位置,为超越离合器的结构优化提供理论依据。

关键词: 流体传动与控制; 有限元方法; 超越离合器; CFD; 动态仿真
中图分类号:TH133.4 文献标志码:A 文章编号:1671-5497(2014)03-0675-05
Dynamic load strength analysis of over-running clutch of dual turbine torque
MA Wen-xing1, HU Jing1, CHU Ya-xu2, WANG Song-lin1, WU Yue-shi1
1. College of Mechanical Science and Engineering, Jilin University, Changchun 130022, China
2. College of Transportation and Civil Engineering, Beihua University, Jilin 132021, China
Fund:
Abstract

The dynamic load strength of over-running clutch of dual-turbine torque converter of a loader was analyzed. First, according to the engine speed and the speed ratio of the torque converter under 12 states in one working cycle, the speeds of I-turbine and II-turbine of the torque converter in each state were calculated. Second, based on the speeds, the torques of I-turbine and II-turbine in each state were calculated in CFD. Thus the stress of the roller, inner ring and outer ring of the over-running clutch in different period of time was calculated. Third, the over-running clutch was dynamically analyzed using finite element method, and the instantaneous stress distribution maps of the roller, inner ring and outer ring of the over-running clutch were obtained. Finally, the maximum stress position was given. This study provides a theoretical basis for the structural optimization of over-running clutch.

Keyword: fluid transmission and control; finite element method; over-running clutch; CFD; dynamic simulation

为了实现无级变速,提高作业生产率,我国轮式装载机大部分都应用双涡轮液力变矩器,它具有变矩比大、高效范围宽等优点。同时超越离合器的锁止与分离可以依据转速差自动实现,以此满足装载机不同工况下传动比的需求。因此,双涡轮液力变矩器广泛地应用于装载机传动系统中[ 1]。

对于超越离合器的强度、刚度的计算问题,传统方法是对于几何形状和受力情况以及约束情况进行简化,然后应用一些简单的公式对简化后的模型进行粗略的计算,因此得出的结论与实际情况差别很大。根据传统计算方法的缺点,选择CFD方法计算出装载机一个循环各时间点所对应的双涡轮液力变矩器Ⅰ涡和Ⅱ涡的转矩,从而得出不同时间内滚柱和内、外圈的受力值。内、外圈通过滚柱来实现摩擦传动,因而传动过程中难免有弹性变形、滑动摩擦及位移等,只进行静力学分析是远远不够的。接触应力有两种求解方法:解析法(Hertz法)和数值法(有限元法),由于Hertz法适合求解几何形状比较规则的物体,而有限元法适合求解复杂的接触问题[ 2, 3],所以本文采用有限元法对超越离合器的强度特性进行分析,提取超越离合器滚柱与内、外圈接触点的瞬时受力曲线,找出影响超越离合器寿命的因素。

1 超越离合器受力的数据提取

表1所示的装载机一个工作循环的测试数据表明:复杂多变的轮式装载机完成一个工作循环大约需要48 s,双涡轮液力变矩器涡轮的转速符合转速的比例传递关系,Ⅰ涡和Ⅱ涡转速可以按照下式计算:

n T=in Bi T (1)

式中:i为变矩器转速比;n B为泵轮转速,r/min;i T为齿轮的传动比(计算Ⅰ涡时,取52/20,计算Ⅱ涡时,取33/39)。

表1 某装载机一个工作循环的测试数据 Table 1 Test data of one working cycle of some loader

将表中发动机转速和变矩器转速比数据代入式(1),计算出各工况下的双涡轮液力变矩器的Ⅰ涡和Ⅱ涡的转速。将双涡轮液力变矩器用UG建模,建立模型后导入CFD中划分网格,采用以四面体为主的方式划分,设置参数求解,将计算好的双涡轮液力变矩器Ⅰ涡和Ⅱ涡的转速代入,计算得到Ⅰ涡和Ⅱ涡的转矩数值,如表2所示。

表2 双涡轮变矩器Ⅰ涡和Ⅱ涡的转速和转矩数据 Table 2 Speed and torque data ofⅠturbine andⅡturbine of dual-turbine torque converter

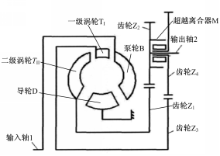
双涡轮液力变矩器的结构原理图如图1所示[ 4]。动力由输入轴1经泵轮B输入,最后经输出轴2输出到变速箱。双涡轮液力变矩器有两个动力输出端,一级涡轮和二级涡轮,其中,一级涡轮经由齿轮Z3、Z4以及超越离合器M将动力传递至输出轴2,二级涡轮TII经过齿轮Z1、Z2和输出轴2连接,始终输出动力到输出轴2。双涡轮液力变矩器一级涡轮和超越离合器的外圈相连,二级涡轮和超越离合器的内圈相连,得到了一级涡轮和二级涡轮的转矩,即得到了超越离合器外圈和内圈的转矩。

图1 双涡轮液力变矩器的结构简图Fig.1 Structure diagram of dual-turbine torque converter

2 超越离合器的动态仿真分析
2.1 超越离合器的计算模型及材料特性

超越离合器的每个滚柱的受力情况大致相同,取一个滚柱的锁止情况进行分析,利用有限元分析软件ANSYS对截取的超越离合器进行网格划分,采用四面体划分法,如图2所示。超越离合器内圈和滚柱采用的材料为GCr15,外圈采用的材料为20CrMnTi,材料特性如表3所示。

图2 超越离合器的网格模型Fig.2 Grid model of over-running clutch

表3 超越离合器的材料特性 Table 3 Material properties of over-running clutch
2.2 基于ANSYS的动态仿真

2.2.1 超越离合器的受力分析及加载曲线

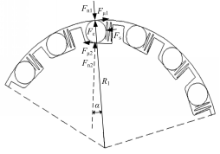
超越离合器的受力分析图如图3所示[ 5],滚柱的受力平衡方程如式(2)所示,传递的转矩大小按式(3)来计算,将超越离合器内圈和外圈所受的转矩换算成滚柱对内、外圈的径向力和切向力,计算的数值如表4所示。

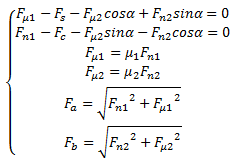(2)

式中:F μ1为外圈对滚柱的摩擦力;F μ2为内圈对滚柱的摩擦力;F n1为外圈对滚柱的正压力;F n2为内圈对滚柱的正压力;F s为弹簧对滚柱的作用力;F c为滚柱离心力; 为外圈与滚柱之间的摩擦因数;μ2为内圈与滚柱之间的摩擦因数;α为超越离合器锁止角;F a为F n1与F μ1的合力;F b为F n2与F μ2的合力。T=nF μ1R1(3)式中:T为超越离合器传递的扭矩;n为滚柱数;R1为外圈与滚柱接触点距旋转中心的距离。

图3 超越离合器结构及滚柱受力示意图Fig.3 Over-running clutch structure and forced-figure of rollerμ1

表4 滚柱所受的径向力和切向力 Table 4 Radial force and tangential force of roller

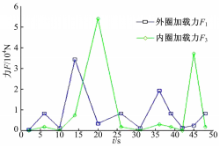
在ANSYS中定义接触对,加动载时采用定义Table的方式,将不同时间内各力值的数据定义到数组中,并采用调用的方式加载。定义约束如下:因为超越离合器外圈安装于输入轴上,故其配合的表面设置为刚性面,外圈表面的节点施加全约束,位移为零。设置完约束后进行参数设置进而求解。依据表4数据绘制的加载曲线如图4所示。图中 F1为滚柱与外圈的加载力曲线, F3为滚柱与内圈的加载力曲线。

图4 超越离合器的加载力曲线Fig.4 Loading curve of overrunning clutch

2.2.2 接触算法的选择

定义接触时,将滚柱与内、外圈设置为面与面的接触,目前解决摩擦接触问题的方法有三种[ 6]。

(1)惩罚函数法(一种近似的方法):

π*=π+α gT g ( α>0) (4)

式中: π *为接触系统的总势能; π为不计接触时的系统势能; α为惩罚因子; g为间隙(其中包括切向间隙),用迭代方法可以精确求解包含接触力的平衡方程,但不能保证其收敛性。

(2) Lagrange乘子法:

π * =π+λ g(5)

式中: λ为 Lagrange乘子,力学意义为接触力。

(3) Lagrange&penalty法。采用 Lagrange& penalty法对超越离合器进行计算,它有惩罚函数法和 Lagrange乘子法的优点,并弥补了其不足。算法如下:

π * =π+λ g +α gT g /2 (6)

3 超越离合器动态仿真结果及分析

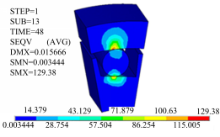
超越离合器的瞬时应力图如图5所示,应力图表明,最大应力出现在滚柱和内、外圈接触处,由于滚柱与内圈一并高速旋转,最高转速可达2000 r/min以上,滚柱高速旋转产生的离心力向外作用于外圈的内表面滚道上,两者的转速差最大可达700 r/min以上,滚柱与外圈齿轮滚道面相互摩擦发热,如果润滑条件不足,很容易造成滚柱或外圈齿轮滚道面的磨损失效,有微小的磨损就会破坏自锁角,从而使超越离合器失效。

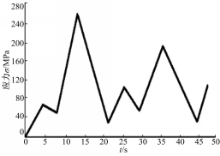
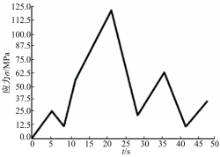
图5 超越离合器的瞬时应力图Fig.5 Instantaneous stress diagram of overrunning clutch

提取滚柱与外圈接触处一节点的瞬时受力放大图,如图6所示。从图6可以看出:5~9 s内受力呈略微下降趋势,说明外圈从开始工作到接触到滚柱发生的是非线性弹性碰撞;10~14 s、19~25 s、30~35 s受力陡增,说明超越离合器开始传递扭矩;在15~21 s、25~30 s、35~45 s时间内,受力陡然下降,说明滚柱受到很大的瞬时冲击力,这直接影响了滚柱的使用寿命,滚柱极易发生疲劳破坏。在5 s、14 s、26 s、36 s、48 s曲线为峰值,这是因为在这些时间点内超越离合器锁止,滚柱与外圈接触处受力较大。图7为滚柱与内圈的瞬时受力曲线。从图7可以看出:在2 s、10 s、42 s时其受力值比较小,这是因为在这些时间点内超越离合器分离,滚柱的离心力向外,滚柱对内圈没有压力的作用。

图6 滚柱与外圈的瞬时受力曲线Fig.6 Instantaneous force curve of roller and outer

图7 滚柱与内圈的瞬时受力曲线Fig.7 Instantaneous force curve of roller and inner

4 结束语

(1)在分析双涡轮液力变矩器超越离合器的结构和工作原理的基础上,提出了一种获得超越离合器转矩数据的方法,并计算获得了不同时间内滚柱所受径向力与切向力的数据。

(2)用有限元方法分析了超越离合器接触区域的状态,通过分析得出了内、外圈与滚柱的瞬时应力分布图,给出产生最大应力的位置,为超越离合器的优化提供了依据。

The authors have declared that no competing interests exist.

参考文献
[1] 刘思妤, 王松林. 国内装载机液力变矩器的未来发展[J]. 建筑机械, 2011(8): 77-79.
Liu Si-yu, Wang Song-lin. Future development of torque convertor for domestic loader[J]. Construction Machinery, 2011(8): 77-79. [本文引用:1] [CJCR: 0.138]
[2] 韩文涛, 张林鹤, 李磊. 有限元方法在汽车设计中的应用[J]. 武警工程学院学报, 2001, 17(4): 33-35.
Han Wen-tao, Zhang Lin-he, Li Lei. Finite element application to vehicle design[J]. Journal of Engineering College of Armed Police Force, 2001, 17(4): 33-35. [本文引用:1]
[3] 潘钰娴, 姜左. 超越离合器滚动接触状态的三维有限元分析[J]. 中国制造业信息化, 2003, 32(12): 108-110.
Pan Yu-xian, Jiang Zuo. 3D FEA of rolling contact model in the overrunning clutch[J]. Manufacture Information Engineering of China, 2003, 32(12): 108-110. [本文引用:1] [CJCR: 0.299]
[4] 才委. 双涡轮液力变矩器转矩分配特性研究[D]. 长春: 吉林大学机械科学与工程学院, 2009.
Cai Wei. Research on the torque distribution characteristics of dual-turbine torque converter[D]. Changchun: College of Mechnical Science and Engineering, Jilin University, 2009. [本文引用:1]
[5] 王松林, 马文星, 胡晶, 等. 双涡轮液力变矩器超越离合器的改进及分析[J]. 吉林大学学版: 工学版, 2013, 43(4): 922-927.
Wang Song-lin, Ma Wen-xing, Hu Jing, et al. Improvement and analysis of over-running clutch of dual-turbine torque converter[J]. Journal of Jilin University(Engineering and Technology Edition), 2013, 43(4): 922-927. [本文引用:1] [CJCR: 0.701]
[6] 陈万吉, 胡志强. 三维摩擦接触问题算法精度和收敛性研究[J]. 大连理工大学学报, 2003, 43(5): 41-547.
Chen Wan-ji, Hu Zhi-qiang. Study of convergence of exact algorithm to solve the three-dimensional frictional contract problems[J]. Journal of Dalian University of Technology, 2003, 43(5): 541-547. [本文引用:1] [CJCR: 0.501]