基于仿生光电<italic>N</italic>点成像理论的大型机组轴系对中在线检测误差模型

引用本文

高艺, 徐成宇, 曹国华. 基于仿生光电N点成像理论的大型机组轴系对中在线检测误差模型 . 2014, 44(3): 692-695
GAO Yi, XU Cheng-yu, CAO Guo-hua. Study on correction model of aligning large-scale machine set to its center based on bionic imaging theory with photoelectric multipoint. 吉林大学学报(工学版), 2014, 44(3): 692-695 复制到剪切板

Permissions

基于仿生光电N点成像理论的大型机组轴系对中在线检测误差模型

高艺, 徐成宇, 曹国华

长春理工大学机电工程学院, 长春130022

曹国华(1965),男,教授,博士生导师.研究方向:工程仿生学.E-mail:caogh@cust.edu.cn

高艺(1968),女,副教授.研究方向:工程装备仿生减阻技术.E-mail:gaoyi@cust.edu.cn

基金:吉林省科技支撑重点项目(20100365); “863”国家高技术研究发展计划项目(2012AAXXX0902);

摘要

基于仿生N点成像理论提出了大型机组对中在线检测误差模型,建立了基于迭代算法的偏微分数值方程组,确定轴瓦最佳调整量,解决了大型机组轴系对中在线检测误校准问题,通过仿真实验验证了检测误差模型的正确性。

关键词: 机电一体化技术; 仿生; 光电; 成像理论; 误差模型

中图分类号:TB17 文献标志码:A 文章编号:1671-5497(2014)03-0692-04

Study on correction model of aligning large-scale machine set to its center based on bionic imaging theory with photoelectric multipoint

GAO Yi, XU Cheng-yu, CAO Guo-hua

Institute of Electromechanical Engineering, Changchun University of Science and Technology, Changchun 130022, China

Fund:

Abstract

A correction model of aligning large-scale machine set to its center is proposed. The model is based on bionic imaging theory with photoelectric multipoint. A numerical partial-differentiation equation set is established based on iterative algorithm to determine the optimal adjustment of the bearing shell. The proposed model can detect and align large-scale machine set to its center. This correction model is verified by simulation experiments.

Keyword: electromechanical integration technology; bionic; photoelectric; imaging theory; correction models

Show Figures

在所有的机械振动事故中,约有60%是由轴系不对中引起或与其有关。大型机组轴系对中技术成熟与否,反映着大型机组制造业水平的高低,轴系对中技术已成为军工、石油、风电、船舶、水利、重机等行业发展的重要影响因素^{[ 1, 2, 3, 4]}。国外已有成熟的激光对中技术并研制出了相关的对中仪器,但国内激光对中技术还亟待发展,国内大部分对中技术还在采用旋转轴方法,即通过反射镜分别测量0°、90°、180°、270°四个值,记录值后通过计算得出轴偏差量进行对中^{[ 5, 6, 7, 8]}。上述方法仅仅将激光对中装置作为对准工具,适用于旋转轴和联轴器的对中调整^{[ 9, 10, 11]},仍需手工计算,在建模、优化、工程算法上还有许多工作要做^{[ 9, 10]}。

本文针对这一问题,研究了基于仿生光电 N点成像理论的大型机组轴系对中在线检测误差理论^{[ 11, 12, 13]},建立了检测系统的轴系对中检测误差数学模型,并进行了优化设计,建立了模型仿真系统,验证了该模型的有效性,仿真结果验证了本文所提出的模型是可行性。

1 对中检测原理

在大型机组激光对中PSD检测中,如果因存在较大的测量操作失误或者存在较大的加工误差,这种传统测三点定圆的测量方式显然不能满足测量精度要求,因此可以基于以上测量理论,将测三点推广至测量 N点,然后利用最小二乘法进行几何中心点拟合。这样既可以增加测量点数,减少因测量操作失误引起的误差,并且由于多点拟合,平均了因为加工原因导致的轴承槽形位误差,使测量和调校工作更具实际意义。给出的 N点拟合的空间直线方程为:

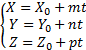(1)

通过此校核方法,采取多点、整体测量,综合数据优化处理;该方法在硬件实现上对检测设被和准直激光的定标位置要求较低,易于实现。

生物的复眼结构,是当单眼感觉到光的刺激后,光点传到神经感受集光器形成“点的影像”,许多单眼的“点的影像”相互作用,就组成“影像”。昆虫的视觉系统虽然相对简单,但却能出色完成视觉检测任务。目前,复眼的工作原理已被成功用于智能机器人、导弹引导装置、激光微加工均束器等。仿生复眼视觉系统体积小、重量轻、视场大,已成为光学领域的研究热点和重要课题^{[ 14]}。

激光对中检测数学模型和轴承槽内表面弦线旋转式激光对中检测数学模型,是在PSD平面法线平行于准直光的假设情况下建立起来的,但在实际工程中只是一种特例,不平行是普遍存在的,二者之间形成的是空间角,该空间角使测量坐标系偏离工作坐标系,测量位置值与角度值都不能反应真实值,因此,需要通过坐标变换校正。

2 仿生校正模型

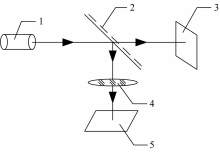
如图1所示,该装置是由激光器1、分束分光镜2、PSD3、透镜4和PSD5组成,激光器1、PSD3位于分束分光镜2的两侧,分束分光镜2的入射面法线方向与水平线的夹角为45°,透镜4的光轴与PSD5法线平行,激光器1发出的一光束,经分束分光镜2透射后,照射在PSD3的光敏面上,经分束分光镜2反射后,再经过透镜4汇聚照射在PSD5的光敏面上。

	Figure Option View Download New Window
	图1 校正检测原理图Fig.1 Detection principle chart correction

如图1所示,在PSD5中,激光靶点在PSD5坐标系中的坐标为(x _T,y _T),设透镜的焦距为f,若轴承槽中心轴相对参考激光光束存在倾斜角ω,它们之间的关系为:

f· tanω=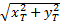

(2)

进而得到实际轴承槽端面与理想轴承槽端面之间的夹角为:

ω= arctan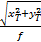

(3)

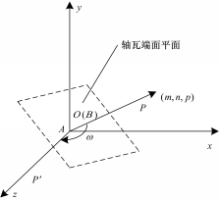
由上述原理,作以下假设:当实际轴承槽端面与理想轴承槽端面的夹角为ω时,拟定轴承槽几何中心为坐标原点,激光束垂直理想轴承槽工作面为坐标系xoy面,理想轴承槽端面法线为z轴,BP为实际轴承槽端面法向量,即方向矢量(m,n,p),如图2所示。图2中:

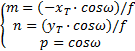(4)

为z轴方向向量,单位向量(0,0,1),由此得到:旋转轴方向矢量为: 。

	Figure Option View Download New Window
	图2 坐标变换法校正机组中心坐标示意图Fig.2 The method of coordinate transform correction unit center coordinate

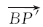
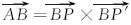
在实际操作过程中,由于PSD3的转动,引起PSD3的坐标系发生α转角变化,如图3所示。在坐标系x'_PSD3oy'_PSD3下点P坐标设为(x'_p31,y'_p31)(即为PSD3显示坐标值),在坐标系x_PSD3oy_PSD3下点P坐标设为(x_p3,y_p3),两者坐标值关系为:

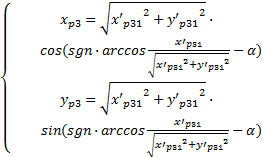(5)

式中:sgn为符号函数;y'_p31≥0时取正1;y'_p31<0取负1。

在图3中,设PSD3中心坐标为O'(x₀,y₀,z₀),激光束打在PSD3上的靶点,在定坐标系中相对于PSD3中心点的定坐标为(x_p3,y_p3,z_p3),并且两点都在实际轴承槽端面上,此平面过定坐标系的原点,且已知其法向量(m,n,p),则有平面方程mx+ny+pz=0,把(x_p3,y_p3)代入平面方程,得到z_p3=-(m·x_p3+n·y_p3)/P,点P相对于轴承槽端面几何中心的坐标为(x_P,y_P,z_P),因为在实际轴承槽端面内有 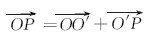,即有:(x_P,y_P,z_P) ^T=(x_p3,y_p3,z_p3) ^T+(x_0,y₀,z₀) ^T,点P(x_p,y_p,z_p)经过旋转矩阵R(ω)旋转到理想轴承槽端面上的坐标为P'(x'_P,y'_P,z'_P),于是有:

(x' _P,y' _P,z' _P )^T=R(ω)·(x _P,y _P,z _P )^T (6)

即:

(x' _P,y' _P,z' _P )^T=R(ω)·( x_P3, y_P3, z_P3)^T+R(ω)·( x₀, y₀, z₀)^T

其中:

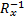
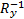
R(ω)=T^-1 (α) (β)R_z(ω)R_y(β)R_x(α)T

上式中的R(ω)·( x_P3, y_P3, z_P3)^T是激光靶点在理想轴承槽端面上相对于PSD3中心的坐标(x'_p3,y'_p3,z'_P3)。

	Figure Option View Download New Window
	图3 转动示意图Fig.3 PSD3 rotation diagram

如图3所示,校正后的坐标(x'_p3,y'_p3)是在坐标系x_PSD3oy_PSD3下的坐标,可利用式(7)把坐标(x'_p3,y'_p3)变换到坐标系x'_PSD3oy'_PSD3下的坐标(x″_p3,y″_p3)(理想轴承槽端面PSD3显示值):

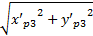
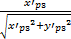
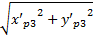
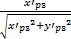
x″_p3= · cos( sgn· arccos +α)y″_p3= · sin( sgn· arccos +α) (7)

式中:sgn为符号函数,y'_p3≥0时取正1,y'_p3<0时取负1。

表1 偏角校正仿真 Table 1 Simulation results mm

根据上述原理,经MATLAB仿真得表1所示的校正值。由表1可得,经坐标变化后得到激光靶点在理想端面内PSD敏感面的坐标值,实现了实际轴承槽端面法线与基准激光束空间夹角的校正。

3 结束语

建立了针对大型机组的对中在线检测误差模型,实现了多点同时采集、整体在线检测误差校正,综合数据时时处理的目标,并通过仿真实验验证了该方法的可行性。为仿生光电 N点成像激光对中检测仪的设计提供了理论模型基础。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Ricardo D. A CMOS optical PSD with submicrometer resolution[J]. Analog Inte-grated Circuits and Signal Processing, 2007, 53: 109-118. [本文引用:1]
[2]	Karpov S. Short time scale pulse stability of the Crab pulsar in the optical band [J]. Astrophysics and Space Science, 2007, 308: 595-599. [本文引用:1] [JCR: 2.064]
[3]	Zhang J Y. High-speed dynamic angular measurement based on position sensitive detector[J]. International Symposium on Instrumentation Science and Technology , 2004, 3: 97-102. [本文引用:1]
[4]	Chien H L. Application of a diffraction grating and position sensitive detectors to the measurement of error motion and angular indexing of an indexing table[J]. Precision Engineering, 2005, 29(4): 440-448. [本文引用:1] [JCR: 1.393]
[5]	Chou H C. Rethinking the three axes alignment theory for direct laryngoscopy[J]. Acta-Anaesthesiologica Scand inavica, 2001, 45(2): 261-266. [本文引用:1]
[6]	Chellappan N, Buckman A Bruce, Vishniac I B. Noise analysis for position sensitive detectors[J]. IEEE Transactions on Instrumentation and Measurement, 1997, 46(5): 1137-1144. [本文引用:1] [JCR: 1.357]
[7]	Knapp W. Measurement uncertainty and machine tool testing[J]. Annals of the CIRP, 2002, 51(l): 459-462. [本文引用:1]
[8]	Khan S A. Development of a position sensitive detector telescope for ERDA based on-line monitoring of swift heavy ions induced modifications[J]. Nuclear Instruments & Methods in Physics Research Section B, 2008, 266(8): 1912-1917. [本文引用:1]
[9]	Jywe W Y. Development of a three -dimensional contouring measuring system and error compensation method for a CNC machine tool[J]. Proceedings of the Institution of Mechanical Engineers Part B Engineering Manufacture, 2007, 221(12): 1755-1761. [本文引用:2]
[10]	Lai X Y. Adaptive control of machining process based on extended entropy square error and wavelet neural network[J]. Journal of Harbin Institute of Technology, 2007, 14(3): 349-353. [本文引用:2] [CJCR: 0.1571]
[11]	任露泉, 孙少明, 徐成宇. 鸮翼前缘非光滑形态消声降噪机理研究[J]. 吉林大学学报: 工学版, 2008, 38(增刊): 126-131. Ren Lu-quan, Sun Shao-ming, Xu Cheng-yu. Noise reduction mechanism of non -smooth leading edge of owl wing[J]. Journal of Jilin University(Engineering and Technology Edition), 2008, 38(sup. ): 126-131. [本文引用:2] [CJCR: 0.701]
[12]	Liu Y, Liu J D, Li S Y, et al. Biomimetic superhydrophobic surface of high adhesion fabricated with micronano binary structure on aluminum alloy[J]. ACS Applied Materials Interfaces, 2013, 5: 8907-8914. [本文引用:1] [JCR: 5.008]
[13]	Qian Z H, Hong Y, Xu C Y, et al. A biological coupling extension model and coupling element identification[J]. Journal of bionic engineering, 2009, 6(2), 186-195. [本文引用:1] [JCR: 1.144] [CJCR: 0.4286]
[14]	任露泉, 梁云虹. 耦合仿生学[M]. 北京: 科学出版社, 2012. [本文引用:1]

2007

0.0

. 2007, 53:109-118 DOI:10.1007/s10470-007-9060-x

A CMOS optical PSD with submicrometer resolution

1.University of Sevilla Instituto de Microelectrónica de Sevilla (IMSE), Centro Nacional de Microelectrónica (CNM-CSIC) Av. Reina Mercedes s/n. Edificio CICA 41012 Sevilla Spain

This paper presents the design of an optical Position Sensing Detector (PSD) for application in biological material gene identification. The system is able to measure changes in the position of a light spot emitted by a Vertical Cavity Surface Emitting Laser (VCSEL). Changes in spot position are produced by the deflections of a microcantilever used to sense the hybridisation process of the biological material. Detection of these deflections requires submicrometer resolution. The photodetectors and the detection algorithm proposed in this paper have been designed and optimized for this resolution. A 0.35 μm CMOS prototype consisting of an array of 22 PSDs has been implemented and experimentally characterized. The obtained results confirm that displacements of the light spot position as low as 0.15 μm can be detected.

... 大型机组轴系对中技术成熟与否,反映着大型机组制造业水平的高低,轴系对中技术已成为军工、石油、风电、船舶、水利、重机等行业发展的重要影响因素^[1,2,3,4] ...

2007

2.064

0.0

. 2007, 308:595-599 DOI:10.1007/s10509-007-9373-3

Short time scale pulse stability of the Crab pulsar in the optical band

1.Special Astrophysical Observatory of RAS Nizhniy Arkhyz 369167 Karachaevo-Cherkessia Russia Nizhniy Arkhyz 369167 Karachaevo-Cherkessia Russia 2.Sternberg Astronomical Institute of MSU 13 Universitetsky pr. Moscow 119992 Russia 13 Universitetsky pr. Moscow 119992 Russia 3.National University of Ireland, Galway University Road Galway Ireland University Road Galway Ireland

The fine structure and the variations of the optical pulse shape and phase of the Crab pulsar are studied on various time scales. The observations have been carried out on 4-m William Hershel and 6-m BTA telescopes with APD photon counter, photomultiplier based 4-channel photometer and PSD based panoramic spectrophotopolarimeter with 1 μs time resolution in 1994, 1999, 2003 and 2005–2006 years. The upper limit on the pulsar precession on Dec 2, 1999 is placed in the 10 s–2 hr time range. The evidence of a varying from set to set fine structure of the main pulse is found in the 1999 and 2003 years data. No such fine structure is detected in the integral pulse shape of 1994, 1999 and 2003 years.

The drastic change of the pulse shape in the 2005–2006 years set is detected along with the pulse shape variability and quasi-periodic phase shifts.

2004

0.0

2005

1.393

0.0

2001

0.0

... 四个值,记录值后通过计算得出轴偏差量进行对中^[5,6,7,8] ...

1997

1.357

0.0

... 四个值,记录值后通过计算得出轴偏差量进行对中^[5,6,7,8] ...

2002

0.0

... 四个值,记录值后通过计算得出轴偏差量进行对中^[5,6,7,8] ...

2008

0.0

... 四个值,记录值后通过计算得出轴偏差量进行对中^[5,6,7,8] ...

2007

0.0

... 上述方法仅仅将激光对中装置作为对准工具,适用于旋转轴和联轴器的对中调整^[9,10,11],仍需手工计算,在建模、优化、工程算法上还有许多工作要做^[9,10] ...

2007

0.0

0.1571

. 2007, 14(3):349-353

Adaptive control of machining process based on extended entropy square error and wavelet neural network

2008

0.0

0.701

. 2008, 38(增刊):126-131

Noise reduction mechanism of non -smooth leading edge of owl wing

Key Laboratory for TerrainMachine Bionics Engineering, Ministry of Education, Jilin University, Changchun 130022, China

The winging noise of the longeared owl was measured, and the results indicated that the circulararc tooth shaped nonsmooth leading edge of its wings has remarkable influence on its flight noise reduction. Applying the reverse reconstruction technique to quantify the geometry information about the nonsmooth leading edge shape of the longeared owl wing, a bionic analogy air foil model was built. A numerical simulation on the noise reduction characterstic of the bionic nonsmooth leading edge airfoil model by computational aeroacoustics method was performed. The airflow noise control mechanism of the bionic nonsmooth airfoil model was studied through the analysis of the influence of the bionic nonsmoothness on the model surface flow field. It was found that comparing with the smooth airfoil model, the bionic nonsmooth airfoil model can reduce the airflow noise level by 5~10 dB, and increase the lift of the airfoil. The reasoons may consist in that the nonsmooth leading edge of the airfoil can rectify the flow around the airfoil and control the boundary layer strippping, reduce the airflow noise from the airflow pressure fluctuation on the airfoil surface and the turbulence breakaway.

长耳鸮扑翼噪声测量试验表明，其翼前缘圆弧齿状非光滑形态对其飞行降噪影响显著。应用逆向重构技术，对长耳鸮翼前缘非光滑形态特征几何信息进行量化，并建立仿生类比模型。采用计算气动声学方法，对仿生前缘非光滑模型的降噪特性进行了数值模拟，并通过分析仿生非光滑形态对模型表面流场的影响，对仿生非光滑形态气流噪声控制机理进行了研究。结果表明，仿生非光滑模型与光滑模型相比，可降低气流噪声5~10 dB，且具备一定的增升作用；仿生前缘非光滑形态具有整流及控制气流分离的特性，可减少由于翼表面气流压力脉动及涡流脱离引发的气流噪声。

... 本文针对这一问题,研究了基于仿生光电N点成像理论的大型机组轴系对中在线检测误差理论^[11,12,13],建立了检测系统的轴系对中检测误差数学模型,并进行了优化设计,建立了模型仿真系统,验证了该模型的有效性,仿真结果验证了本文所提出的模型是可行性 ...

2013

5.008

0.0

2009

1.144

0.4286

. 2009, 6(2):186-195

A biological coupling extension model and coupling element identification

2012

0.0

... 仿生复眼视觉系统体积小、重量轻、视场大,已成为光学领域的研究热点和重要课题^[14] ...