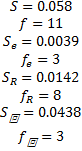王骥月(1989),女,博士研究生.研究方向:仿生科学与技术.E-mail:jywang12@mails.jlu.edu.cn
基于蝉上颚口针表面的非光滑结构形态,结合对蝉口针刺入机理的分析,设计出锯齿形仿生针头。采用二元二次回归正交组合试验优化设计方法,研究了锯齿宽度、锯齿间距这两个仿生结构参数对针头穿刺阻力的影响规律,求取了回归方程。得到最优仿生锯齿形针头的结构参数为:锯齿宽度0.3 mm、锯齿间距2.5 mm,减阻率为43.21%。锯齿形仿生针头通过减小接触面积、形成滚动轴承模型和产生微震的方式实现减阻效果,为无痛仿生针头的研制提供了依据。
The penetration mechanism of the mandibular stylet of cicada with non-smooth shape is analyzed. A bionic needle with saw tooth, which is inspired by cicada stylet is designed. The binary quadratic regression and orthogonal combination test optimization design method are employed to research the influences of two bionic structural parameters, the width of serrate and the interval of serrate, on the puncture resistance of syringe needle. A regression equation of the cicada stylet is obtained. The structure parameters of the optimal bionic saw tooth needle are that the width of serrate is 0.3 mm and the interval of serrate is 2.5 mm, and its drag reduction rate is 43.21%. The drag reduction effect of the saw tooth bionic needles is attributed to the decreasing contact area, forming rolling bearing model and producing microseism. This study provides the basis for the development of bionic painless needles.
目前,已有的无痛注射方式主要有:①微针注射[ 1]。通过减小针管尺寸,达到无痛注射目的[ 2]。但针管直径小限制了药物的吸收效果,使微针注射的适用范围仅限于少量、高效的药物[ 3]。②激光注射[ 4]。借助激光去除微量表皮,实现无痛注射。但此方法适用药品单一,难以大范围推广。③无针注射[ 5]。通过高压射流将药物颗粒直接打入皮下。由于需要较多辅助仪器、成本较高[ 6]。④快速注射[ 7]。采用医疗上进针快、推药慢、拔针快的二快一慢法,能够在一定程度上缓解注射痛感。但此法受患者主观因素影响较大,且对不同患者使用时效果不稳定,减痛成效不够理想。⑤经络推拿及学位按压[ 8]。通过经络推拿和学位按压的方式减缓注射疼痛的一种技术手法。但此方法并不适用于所有人,如孕妇,所以只能作为减痛的辅助手段。⑥仿生针头。结合蚊子口针刺入皮肤过程的受力分析[ 9],模仿蚊子口针表面非光滑结构,设计得到凹槽形仿生针头,通过减小针头刺入阻力的方式,达到减痛或无痛注射效果[ 10]。与以往无痛技术不同,仿生无痛针头是在传统针头基础上进行的仿生设计,不改变原有针头尺寸[ 11],不影响注射药物量与治疗效果,无需额外辅助设备,能使注射达到无痛或减痛的效果[ 12],易被恐针及痛阈低的患者接受,为无痛针头开发提供了新的研究途径。
本文以蝉口针为仿生对象,经过仿生针头结构优化设计和减阻机理分析,得到减阻效果与仿生结构间的函数关系式,获得具有最佳减阻效果的仿生针头结构参数,对于无痛仿生针头的研制具有重要意义。
蝉以植物汁液为食,通过两个上颚口针交替刺入植物组织内部,吸取汁液。蝉上颚口针表面存在着有序非光滑结构,其中以口针中部的锯齿形结构最为规则、突出(见图1),锯齿间距与锯齿宽度大小相等,约为5 μm,齿高约为4 μm,锯齿排布均匀。经过分析,得到锯齿形非光滑结构在口针刺入过程中的作用主要有以下两点:①锯齿形结构的存在使得口针刺入植物过程中,口针与植物体间的接触面积减小,由蝉口针刺入力式(1)[ 13]可知,减小接触面积可直接减小口针刺入力, 使刺入能力增加;②锯齿形结构的存在允许植物汁液进入锯齿结构凹陷处,在刺入过程中起到润滑作用,让刺入动作变得更为容易。
F i=τG pA+θ (1)
式中: Fi为口针刺入力; A为口针与植物接触面积; Gp为植物的断裂韧性;τ、θ分别为与口针尺寸有关的参数。
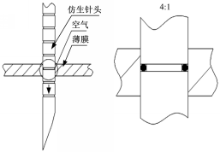
提取蝉上颚口针中部的锯齿形结构作为仿生对象,进行仿生针头结构设计,在标准16号针头外壁上加工出仿生锯齿形非光滑结构。
图2为锯齿形仿生针头加工示意图和实物图,其中W为锯齿宽度,D为锯齿间距。由于针壁较薄,约为0.1 mm,齿深对试验结果影响较小,可忽略不计,所以在保证针头强度的前提下,确定加工长度为30 mm,加工深度为0.04 mm,针尖部分不加工。
以2 mm厚硅胶薄膜作为仿真生物体组织模型,应用北京卓川电子科技有限公司生产的医用注射针刺穿力测试仪(CL15822-E),根据GB 18671-2009一次性使用静脉输液针国家标准[ 14],进行锯齿形仿生针头穿刺阻力试验。试验过程中,首先对标准光滑针头进行编号和穿刺阻力试验;然后根据设计参数在标准光滑针头表面上加工锯齿形仿生结构,得到锯齿形仿生针头;之后进行仿生针头穿刺阻力试验;最后进行数据处理与统计,利用式(2)求出每支针头的减阻率,每种结构参数加工三支针头,取减阻率平均值作为试验结果。
G= 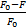
式中:G为减阻率;F0为光滑针头穿刺阻力;F为仿生针头穿刺阻力。
为了研究仿生结构参数与减阻效果之间的变化规律, 采用二元二次回归正交组合试验优化设计方法[ 15],研究锯齿宽度、锯齿间距与减阻率之间的函数关系,锯齿宽度变化范围为0.06~0.3 mm,锯齿间距变化范围为0.5~2.5 mm。表1为锯齿形仿生针头结构参数编码表。表2为二元二次回归正交组合设计试验方案及计算格式表。
中心化处理公式为:
x'ij= 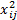
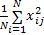
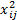
式中:N为试验次数;x'ij为xij的编码值; 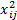
| 表1 锯齿形仿生针头自然因素水平及其编码表 Table 1 Natural factors level and its coding of the saw tooth bionic needle |
| 表2 二元二次回归正交组合设计试验方案及计算格式表 Table 2 Test program and calculation format of binary quadratic regression and orthogonal combination design |
表1中,zj为j因素;xj为j因素编码值;;z2j为j因素最大水平;z1j为j因素最小水平;z0j为j因素中心水平;Δj为j因素水平间隔;r为臂长,本文r=1.21;z0j+Δj为j因素上水平;z0j-Δj为j因素下水平,xj= 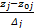
表2中,xj(zj)为第j个因素的编码因素;x1x2为两个编码因素的交互作用;y为穿刺轴向阻力减阻率;bj为回归系数;Sj为各因素的偏差平方和;Fj为回归系数F检验;αj为显著性水平。
由此,得到编码空间回归方程为:

然后,对回归方程进行显著性检验:
F回= 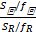
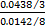
F lf= 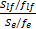
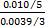
得知回归方程(4)的置信度为99%。经失拟检验知回归方程不失拟。
最后,将编码公式和中心化处理公式(3)代入回归方程(4),得到自然空间回归方程为:
 | (5) |
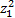
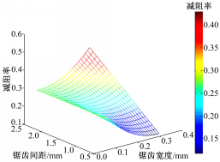
为了方便分析仿生针头减阻机理,根据回归方程(5),绘制如图3所示的锯齿形仿生针头试验优化设计结果,由图可知:当锯齿宽度在0.06~0.3 mm、锯齿间距在0.5~2.5 mm内变化时,由锯齿宽度、锯齿间距、两者交互作用和锯齿宽度二次项共同作用可使减阻率恒为正;最大减阻率为43.21%,此时锯齿宽度为0.3 mm、锯齿间距为2.5 mm。
由仿生针头减阻试验可知,锯齿形仿生针头均具有减阻效果,这是由于:针头穿刺过程中的摩擦力f符合库伦公式[ 16]:
f=CA+N tanβ (6)
式中:f为针头穿刺过程中所受摩擦力;C为薄膜的粘附力;A为针头与薄膜接触面积;N为针头穿刺过程中所受正压力;β为针头与薄膜间的摩擦角。
穿刺过程中,锯齿形仿生非光滑结构的存在使针头外壁与刺入对象(2 mm硅胶薄膜)间的接触面积减小,而针头所受正压力N、摩擦角β和薄膜粘附力C不受仿生非光滑结构影响,因此,针头所受摩擦力f减小,即表现出减阻效果。
锯齿形非光滑结构允许空气存在于锯齿凹陷处,在刺入薄膜过程中,针头外壁、空气、薄膜三者形成滚动轴承模型[ 17](见图4),与标准光滑针头穿刺时的滑动摩擦相比,仿生针头所受的摩擦力减小。
 | 图4 锯齿形仿生针头、空气和薄膜形成的滚动轴承模型Fig.4 Rolling bearing model formed by the saw toothbionic needle,the air and the film |
实际应用中,锯齿形仿生针头的刺入对象是生物体病患,此时,生物体液会将锯齿凹陷处的空气挤出,代替空气的位置与针壁、皮肤组织共同形成与滚动轴承减阻机理相同的模型。与此同时,体液的存在会对针头的刺入起到润滑作用,有一定的减阻效果,而锯齿形结构的非光滑特性会导致皮肤组织产生垂直于针头轴向的微震,加速体液流动,增大减阻效果。
(1)蝉上颚口针具有锯齿形非光滑结构,既能使口针与植物的实际接触面积减小、刺入能力增加;又能允许植物汁液进入锯齿结构凹陷处,在刺入过程中起到润滑作用。
(2)对锯齿形仿生针头进行二元二次回归正交组合优化设计,得到其回归方程。
(3)锯齿形仿生针头在锯齿宽度为0.3 mm、锯齿间距为2.5 mm时,减阻率可达43.21%。
(4)锯齿形非光滑结构使仿生针头与薄膜间的接触面积减小,减小穿刺阻力;锯齿形非光滑结构允许空气存于锯齿凹陷处,使针头外壁、空气、薄膜三者形成与滚动轴承减阻机理相同的模型,有效地减小了穿刺摩擦阻力;锯齿形结构的非光滑特性会使皮肤组织产生垂直于针头轴向的微震,加速体液流动,增大体液润滑效果。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|




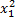 (x'1)
(x'1)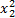 (x'2)
(x'2)