引用本文
马喜强, 刘维亚, 郑喜凤, 程鹏. 非平稳多任务下的动态功耗管理随机策略. 2014, 44(3): 776-781
MA Xi-qiang, LIU Wei-ya, ZHENG Xi-feng, CHENG Peng. Dynamic power management stochastic policy for non-stationary multi-task. 吉林大学学报(工学版), 2014, 44(3): 776-781  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
非平稳多任务下的动态功耗管理随机策略
马喜强1,2, 刘维亚1, 郑喜凤1, 程鹏1,2
1.中国科学院 长春光学精密机械与物理研究所,长春 130033
2.中国科学院大学,北京 100039

马喜强(1986),男,博士研究生.研究方向:嵌入式系统的低功耗.E-mail:maxiqiang200@sina.com

基金:国家科技支撑计划项目(2009BAE73B01);
摘要

基于系统信息建立了任务的设备利用率统计查找表,并根据实际的间隔时间更新分布。然后,建立了半Markov随机模型,定义了代价函数和目标优化函数,并给出了平均准则下基于线性规划的求取最优策略的方法。试验结果表明:在考虑性能约束的条件下,该算法具有很好的稳定性;延迟率小于0.10;竞争率可以达到0.57。更稳定、有效地降低了功耗,有利于在嵌入式系统中应用。

关键词: 计算机应用; 动态功耗管理; Markov决策过程; 策略优化; 嵌入式系统
中图分类号:TP301 文献标志码:A 文章编号:1671-5497(2014)03-0776-06
Dynamic power management stochastic policy for non-stationary multi-task
MA Xi-qiang1,2, LIU Wei-ya1, ZHENG Xi-feng1, CHENG Peng1,2
1. Changchun Institute of Optic,Fine Mechanics and Physics,Chinese Academy of Sciences,Changchun 130033,China;
2. University of Chinese Academy of Sciences,Beijing 100039,China
Fund:
Abstract

A dynamic power management stochastic policy for non-stationary multi-task is proposed. First, device-requester utilization lookup table was constructed based on system message, and distribution was updated according to the actual time interval. Then, a Semi-Markov stochastic model was built, and the cost function and objective function were defined. The discount criteria optimization method based on linear programming strategy was given. The moment of decision and conversion state was pointed out. Experimental results show that, while considering the conditions of the performance constraints, the algorithm has good stability; delay rate is less than 0.10; competitive rate can reach 0.57. The algorithm reduces power consumption more efficiently than other policies, and is beneficial to the application in embedded systems.

Keyword: computer application; dynamic power management; Markov decision processes; policy optimization; embedded system
0 引言

随着半导体技术的发展和嵌入式设备性能的提高,系统性能约束下的功耗问题成为嵌入式系统研究的焦点[ 1, 2, 3]。现阶段,系统设计中通用的低功耗策略包括动态功耗管理(Dynamic power management,DPM)和动态电压调节(Dynamic voltage scaling,DVS)。通常情况下,把DVS也作为DPM的一种来看待[ 4]。

DPM策略大体上可分为3类:①Timeout超时策略。基本思想是在负载经过一段超时阈值后将负载置为低功耗状态,包括固定超时阈值策略和自适应超时阈值策略[ 5, 6, 7, 8]。②Predict预测策略。其本质是在做出决策前对本次空闲时间长度进行预测,如果预测值足够大,就直接将PMC(Power manageable component)切换到相应的休眠模式[ 9]。③随机Markov策略。通过建立Markov模型来描述系统设备操作请求和设备服务的随机行为,把DPM决策问题看成一个受控马氏链问题,从而更准确地选择决策时刻和设备转换状态。

Timeout超时策略具有原理简单应用广泛的特点,但它是一种探索式策略。Predict预测策略一旦阈值预测不准确,则可能会适得其反,增大功耗。随机Markov策略根据建立的DPM决策模型可分为:基于马尔可夫修正随机过程的层次DPM模型[ 10];基于连续时间的马尔可夫决策过程DPM模型[ 11];基于离散时间的马尔可夫决策过程DPM模型[ 12]。以上策略均忽略了远距离历史效应,并且均未考虑多任务下系统负载的非平稳问题。多任务下系统负载的非平稳特性是指不同任务使用设备的方式和任务执行的顺序有差别而使设备负载表现出的随机性。基于时间索引的半马尔可夫决策过程DPM模型[ 13]虽然加入了历史事件的参数,但其本质属于一种随机超时策略。

吴琦等从理论上证明了DPM最优策略是确定性马尔可夫策略[ 14],并说明了超时策略具有很好功耗性能的原因,但其DPM模型忽略了状态转换间的延时,其DPM控制算法本质上属于超时策略,并且假设空闲时间长度服从Pareto分布,有一定的局限性。本文针对非平稳多任务下的动态电源管理问题,提出了SMBSP(System message based stochastic policy)算法。该算法在分析系统任务的设备利用率的基础上建立了半Markov随机模型,并给出了该随机模型下的在线优化方法。半Markov控制过程模型对系统的动态特性描述精确,优化算法不依赖系统参数的信息,自适应性强。该算法能够同时给出功耗转换状态及转换时刻。通过OMAP-L137平台动态电源管理的应用试验可验证算法的有效性。

1 任务的设备利用率

线程(本文对线程和进程不做区分)的执行可以根据设备的应用程序接口函数被调用地址进行划分,堆栈(stack)反映了线程的调用过程,可以采用栈深(stack depth)和返回地址(return address)来联合区分设备唯一调用路径[ 15]。堆栈深是指当前栈指针(即当前sp寄存器的内容)与初始栈指针的差值,返回地址是指当前链接寄存器中的内容,这些可以从线程保存的上下文中获取。这样可以根据应用程序接口函数调用的堆栈深度和返回地址来联合预测任务的设备使用率,用U(d,r)表示任务的设备利用率(即与系统历史堆栈深度和返回地址相关程度),定义如下:

U(d,r)n=aU(d,r)+(1-a)U(d,r)n-1(1)

式中:a为折扣因子,根据试验a取值为0.2~0.8[ 16]。

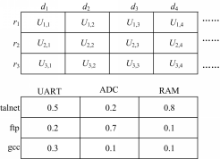
以U(d,r)为元素建立统计查找表,则查找表中保存的分布信息即为所需的各线程设备操作时间间隔分布,即当前任务使用设备时间占设备总工作时间的比例,查找表结构如图1所示,图中还给出了一个包括3个任务(telnet、ftp和gcc)和3个设备(UART、ADC和RAM)的查找表实例,每次操作请求到来时根据返回地址和堆栈深度匹配查找表,并根据实际的任务设备利用率更新设备查找表。

图1 基于系统信息的设备查找表和实例Fig.1 Lookup table of a device corresponding to system message and an example

2 SMBSP算法
2.1 半Markov随机模型

DPM随机模型主要有离散时间马氏决策过程、半马氏决策过程和连续时间马氏决策过程[ 17]。在离散时间马氏决策过程中,忽略了时间因素,有一定的局限性,连续时间马氏决策过程中的状态转移函数在系统的DPM问题中是很难确定的,而半马氏决策过程对时间分布函数和代价函数的假设与DPM问题是一一对应的,因此,半马尔可夫随机模型是最优的DPM随机模型[ 18]。本文DPM模型采用离散时间的半Markov决策模型,时间被描述为一连串离散值,假设设备有N种低功耗模式,分别由m0,m1,…,mN表示,则系统状态变化过程可以由如下的半马尔可夫过程描述:

{S,A(i),Pij(a),T(·|i,a,j),r(u,i,a,j,t),V;i,j∈S,a∈A(i)} (2)

式中各元素的定义如下:

(1)系统状态集

S={(tn,mn)|n=0,1,…,N} (3)

(2)决策集A(i)是状态为i∈S时的功耗管理器可用命令集合。

(3)Pij(a)为转换概率,指当前状态为i采取决策a∈A(i)时,下一状态为j的概率。

(4)T(·|i,a,j)为从状态i转移到状态j所需的时间分布函数,分布函数可以从上节建立的查找表中获得。定义期望逗留时间为:

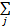
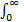
τ(i,a)= pij(a) tT( dt|i,a,j) (4)

(5)r(u,i,a,j,t)是代价函数,指状态为i采取决策a,且转移时间为t的条件下,系统在时间段[0,u]中(u≤t)的功耗,其函数定义为:

r(u,i,a,j,t)=r1(i,a,j)+r2(i,a,j)u (5)

式中:r1(i,a,j)为状态转换延时功耗;r2(i,a,j)为在转移途中单位时间内功耗。

(6)V为目标优化函数。

V(π,i)=

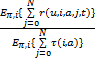(6)

2.2 Markov策略优化

定义1 记( ,m0)为初始状态(假定此时为最低功耗状态),下一次进入最低功耗的状态为终止状态,记为( ,m0),将从初始状态到终止状态定义为一个决策周期。

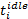
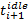
通过定义1就把无限时段的半Markov决策过程转换为有限时段的半Markov决策过程。

如果状态空间上的概率分布函数族δ(n)满足:对每个tn时刻的i∈S,δ(n)(·|i)是决策集A(i)上的一个概率分布,即满足δ(n)(a|i)≥0和 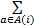δ(n)(a|i)=1,那么称 δ( n)为一个 Markov决策过程。系统的一个策略 π是指一个序列 π=[ δ(1), δ(2),…],即各决策时刻采取的决策组成的序列。所有的策略构成策略空间 Π, DPM问题就是求取 V( π)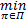最小值的策略 π *。

V( π *) = V(π) (7)

定义功耗和性能损失向量:

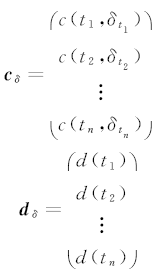(8)

策略优化的实质是性能约束下的功耗优化,本文采用折扣模型进行分析。

对策略 π和固定的折扣因子 β( β<1),系统在第 n个决策周期的 d和 c的折扣期望为:

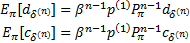(9)

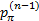
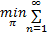
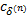
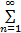
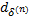
式中:p(1)为系统在初始时刻t1的状态概率分布; 为在策略下π,从决策周期0到周期n-1的转移矩阵。因此,性能约束下的功耗优化问题可用式(10)描述:

E π[ ]s.t. E π[ ]≤ D(10)

式中:约束值 D为根据系统的工作历史求出的性能约束的期望值。

折扣准则下式(10)转化为式(11)的线性规划问题( Linear programming, LP)。

V( π, i)s.t. f i, a -β ( a) f j, a = ≤

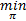
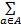
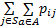
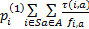
D f i, a≥0, i∈ S(11)

式中: f i, a为在 i状态下发出命令 a的频率; β表示系统继续运行的概率; 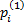为系统初始状态为 i的概率。

对线性规划(11)采取两阶段法的单纯形法求解 f i, a,第1阶段引入人工变量,构造一个辅助的目标函数,以求解原始线性规划问题的初始基本可行解;第2阶段迭代求解原始线性规划问题的目标函数,直到达到最优解为止。最优策略 V( π *)中的元素 V i, a可由式(12)计算得出:

V i, a =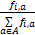(12)

3 试验结果

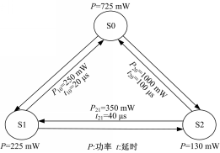
为了评估策略的节能效果和对性能的影响,本文采用 OMAP-L137平台作为试验对象,将本文算法与不同超时阈值的超时策略、预测策略和随机策略进行比较。 OMAP-L137应用处理器采用浮点 DSP与 ARM9相结合的架构,提供用于联网的各种外设,并运行 Linux或 DSP/BIOS实时内核以实现操作系统灵活性,还可在极低的功耗水平下工作,图2给出了浮点 DSP核的 PSM( Power state machine)模型。各个状态均标有相应的功耗,边线上标出了状态转换所需要的时间及切换功耗。

图2 某型射击诸元计算器的PSM模型Fig.2 PSM module of artillery firing data calculator

在本文的试验环境中,为验证效果产生了6个不同的任务列,各任务在N个时间段内的设备利用率统计查找表如表1所示(一个时间段即一个决策周期,N取1000)。

每个任务列分别应用以下电源管理策略(其中平衡时间[ 19]定义为T be):

(1)Timeout:超时阈值=T be的固定时限超时策略,达到超时时间值时直接转为S2低功耗状态。

(2)CTMDP[ 11]:连续时间Markov随机策略。

(3)Predict[ 16]:Hwang的指数平均法(预测策略),取 a=0.5,使最近的历史和先前的历史有相等的权值,达到预测时间值时直接转为S2低功耗状态。

(4)Adaptive[ 5]:超时阈值=T be的自适应DPM策略,达到超时阈值时直接转为S2低功耗状态。

(5)DTMDP[ 12]:离散时间Markov随机策略。

(6)Ours:本文策略。

表1 基于系统信息的时间序列概率统计 Table 1 Time series of probability statistics based on system message

采用竞争率作为功耗评估指标,延迟率作为性能指标,命中率作为策略的预测效率指标,分别定义如下:

竞争率ζ=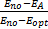(13)

式中:E A为当前策略的能耗;E no为无策略的能耗;E opt为最优离线策略下的能耗。

延迟率δ=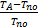(14)

式中:T A为当前策略下的总时间;T no为无策略时的总时间。

命中率η=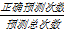(15)

竞争率ζ表示当前策略相对于最优策略的功耗效率,各策略的竞争率比较如图3(a)所示,从图中可以看出,本文策略的功耗效率是显著的,平均值达到了0.57,高出自适应策略3个百分点。CTMDP具有最低的功耗效率,这是因为CTMDP策略是基于用户到达服从指数分布的假定,导致长的空闲时间缺失和设备关闭次数增加,并且该策略还需要周期性的模型计算,消耗了大量的能量。

各策略的延迟率和命中率比较分别如图3(b)和图3(c)所示,Adaptive策略拥有较低的延迟率和较高的命中率,Predict策略的竞争率有较大的波动性。超时策略只有准确选择超时阈值时,节能效果才趋近于最优,否则效果十分不理想,对同一系统进行决策时,其估计值有可能不同,所以准确的超时阈值是很难得到的。从整体上看,除本文策略延迟率小于0.1外,其他策略都超过了0.15。

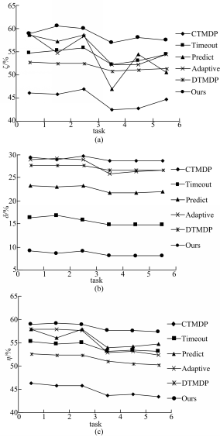图3 各策略的竞争率、延迟率和命中率比较Fig.3 Comparison of competitive ratios,delay ratios and hit ratios for all policies

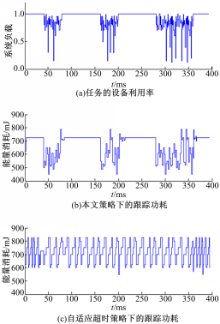
为了进一步探讨本文策略与实际负载的相互关系,产生了4个任务(两个周期性任务和两个非周期性任务),系统负载实际跟踪曲线如图4所示(只列出了自适应超时策略和本文策略的效果对比)。从图中可以看出本文策略有较好的鲁棒性,这是因为本文策略是基于任务级的,并且唤醒设备是事件驱动的,与具体的设备无关。

图4 系统负载实际跟踪功耗比较Fig.4 Comparison of energy consumption with system trace

在考虑性能损失的条件下,假定初始时刻设备处于S1模式,无请求且队列为空,则初始概率分布为 b=(1,0,0,0,0,…,0)T。设折扣因子 β=0.8,基于系统信息的时间序列概率统计如表1所示,则根据式(10)和(11)求解该线性规划得到各决策周期(取前12个决策周期)内的最优策略如下:

π(S1)→π(S1)→π(S1)→π(S0)→π(S2)→π(S2)→π(S0)→π(S0)→π(S2)→π(S2)→π(S2)→π(S1)

4 结束语

针对嵌入式系统的多任务环境下的非平稳特性,提出了一种SMBSP算法,通过堆栈深度和返回地址来联合区分设备调用路径,采用基于任务级的随机半Markov模型进行决策。本文给出的随机最优算法不受空闲时间长度的分布限制,可以适用于一般分布,给出了确定决策时刻和选择决策策略的方法,算法计算量小,在节能和系统性能之间找到了折衷切入点。需要指出的是,试验最后部分得到的策略适当地简化了系统模型,其结果仅具有参考性;其次,基于系统信息的马尔可夫模型是对一个复杂的随机过程的概率估计,对于同一系统其估计值有可能不同,但通过本文算法得到的最终策略都是趋近于最优的。试验结果表明:本文策略的延迟率小于0.10,竞争率可以达到0.57。有利于在嵌入式系统中应用。

The authors have declared that no competing interests exist.

参考文献
[1] Soteriou V, Peh L S. Dynamic power management for power optimization of interconnection networks using on/off links[C]∥11th Symposium on High Performance Interconnects, Stanford, C A, USA, 2003: 15-20. [本文引用:1]
[2] Kachroo P, Shukla S K, Erbes T, et al. Stochastic learning feedback hybrid automata for power management in embedded systems[C]∥Proceedings of the 2003 IEEE International Workshop on Soft Computing in Industrial Applications, Binghamton, N Y, USA, 2003: 121-125. [本文引用:1]
[3] Weng L C, Wang X J, Liu B. A survey of dynamic power optimization techniques[C]∥3rd IEEE International Workshop on System-on-Chip for Real-Time Applications, Calgary, Alberta, Canada, 2003: 48-52. [本文引用:1]
[4] Benini L, De Micheli G. System-level power optimization: techniques and tools[J]. ACM Transactions on Design Automation of Electronic Systems, 2000, 5(2): 115-192. [本文引用:1] [JCR: 0.522]
[5] Lu Y H, De Micheli G. Comparing system-level power management policies[J]. IEEE Design & Test of Computers, 2001, 18(2): 10-19. [本文引用:2] [JCR: 1.623]
[6] Krishnan P, Long P M, Vitter J S. Adaptive disk spin-down via optimal rent-to-buy in probabilistic environments[J]. Algorithmica, 1999, 23(1): 31-56. [本文引用:1] [JCR: 0.488]
[7] 王毅, 张德运, 马新新, 等. 无线传感器网络传感器节点动态功耗管理方法[J]. 吉林大学学报: 工学版, 2008, 38(4): 880-885.
Wang Yi, Zhang De-yun, Ma Xin-xin, et al. Novel dynamic power management of sensor node in wireless sensor networks[J]. Journal of Jilin University(Engineering and Technology Edition), 2008, 38(4): 880-885. [本文引用:1] [CJCR: 0.701]
[8] Helmbold D P, Long D D E, Sconyers T L, et al. Adaptive disk spin-down for mobile computers[J]. Mobile Networks & Applications, 2000, 5(4): 285-297. [本文引用:1] [JCR: 1.109]
[9] Srivastava M B, Chand rakasan A P, Brodersen R W. Predictive system shutdown and other architectural techniques for energy efficient programmable computation[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 1996, 4(1): 42-55. [本文引用:1] [JCR: 1.218]
[10] Ren Z Y, Krogh B H, Marculescu R. Hierarchical adaptive dynamic power management[J]. IEEE Transactions on Computers, 2005, 54(4): 409-420. [本文引用:1] [JCR: 1.379]
[11] 江琦, 奚宏生, 殷保群. 动态电源管理的随机切换模型与策略优化[J]. 计算机辅助设计与图形学学报, 2006, 18(5): 680-686.
Jiang Qi, Xi Hong-sheng, Yin Bao-qun. Stochastic switching model and policy optimization for dynamic power management[J]. Journal of Computer-aided Design & Computer Graphics, 2006, 18(5): 680-686. [本文引用:2] [JCR: 3.172]
[12] Benini L, Bogliolo A, Paleologo G A, et al. Policy optimization for dynamic power management[J]. IEEE Transactions on Computer-aided Design of Integrated Circuits and Systems, 1999, 18(6): 813-833. [本文引用:2] [JCR: 1.093]
[13] Simunic T, Benini L, Glynn P, et al. Event-driven power management[J]. IEEE Transactions on Computer-aided Design of Integrated Circuits and Systems, 2001, 20(7): 840-857. [本文引用:1] [JCR: 1.093]
[14] 吴琦, 熊光泽. 非平稳自相似业务下自适应动态功耗管理[J]. 软件学报, 2005, 16(8): 1499-1505.
Wu Qi, Xiong Guang-ze. Adaptive dynamic power management for non-stationary self similar requests[J]. Journal of Software, 2005, 16(8): 1499-1505. [本文引用:1] [CJCR: 2.181]
[15] 戚隆宁, 张哲, 黄少珉. 多任务下I/O设备的动态功耗管理[J]. 中国工程科学, 2008, 10(2): 60-65.
Qi Long-ning, Zhang Zhe, Huang Shao-min. Dynamic power management for I/O devices under multi-task environment[J]. Engineering Science, 2008, 10(2): 60-65. [本文引用:1] [CJCR: 0.658]
[16] Hwang C H, Wu A C H. A predictive system shutdown method for energy saving of event-driven computation[J]. ACM Transactions on Design Automation of Electronic Systems, 2000, 5(2): 226-241. [本文引用:2] [JCR: 0.522]
[17] 唐昊, 吴玉华, 周雷. 半Markov决策过程的数值迭代优化[J]. 吉林大学学报: 工学版, 2006, 36(1): 108-112.
Tang Hao, Wu Yu-hua, Zhou Lei. Value iteration optimization for Semi-Markov decision processes[J]. Journal of Jilin University (Engineering and Technology Edition), 2006, 36(1): 108-112. [本文引用:1] [CJCR: 0.701]
[18] 胡奇英, 刘建庸. 马尔可夫决策过程引论[M]. 西安: 西安电子科技大学出版社, 2002. [本文引用:1]
[19] Lee W K, Lee S W, Siew W O. Hybrid model for dynamic power management[J]. IEEE Transactions on Consumer Electronics, 2009, 55(2): 656-664. [本文引用:1] [JCR: 1.087]