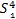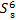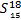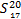郑寇全(1983),男,博士.研究方向:智能信息处理.E-mail:zhengkouquan0421@163.com
通过引入滑动窗口机制和矢量量化技术,较好地解决了直觉模糊规则零匹配的问题,准确反映了不确定时序系统数据的分布特性,提高了复杂环境下时间序列长期趋势预测的精度,扩展了直觉模糊时间序列预测理论的应用范围。最后通过典型实例验证了该方法的有效性和优越性。
A new method for long-term Intuitionistic Fuzzy Time Series (IFTS) forecasting is proposed. By employing the sliding window scheme and vector quantization technique, the non-matching problem of intuitionistic fuzzy rules is solved efficiently. Meanwhile, the distribution characters of the uncertain time series data system are reflected accurately. The long-term forecasting accuracy of time series in the complex environment is improved, thus greatly extending the IFTS forecasting application. Finally, the experimental results validate the efficiency and advantage of the proposed algorithm.
时间序列是指随时间变化的具有随机性且前后相互关联的动态数据序列,时间序列分析是用概率论与数理统计的方法研究序列数据关联规律的科学理论[ 1]。现实世界的随机性、缺乏相关属性(参数)以及信息不精确等因素的广泛存在,使得随机理论已无法有效描述和处理样本数据的模糊不确定性。Song[ 2]将序列变量设定为模糊数,首次提出了模糊时间序列(Fuzzy time series,FTS)的概念。由于能较好地处理含糊和不完整的模糊信息,模型具有较强的鲁棒性和兼容性,FTS预测得到了相关领域的重点关注,并与其他优化理论相融合产生了多种改进算法:Singh[ 3]构建了时间不变性FTS预测模型;Bai[ 4]提出了启发式时间不变性FTS预测方法;Aladag[ 5]结合自适应期望和人工神经网络建立了FTS混合预测模型;Li[ 6]将FTS预测扩展到长期时间范围,初步建立了长期FTS预测模型。然而,随着FTS预测理论的日趋成熟,其局限性也逐渐显现:普通模糊集隶属度单一,不能有效描述和表征序列数据的实时模糊变化趋势;等间距论域区间划分无法反映连续数据分布不均匀的特性;FTS预测性能大多局限于短期时间范围,即使少数模型尝试进行长期趋势预测,却均是基于多输入单输出映射,为不同时间范围建立不同的模型,这样不仅增加了系统的复杂度,忽略了预测值间的随机依赖性,且易造成误差积累。因此,FTS预测理论的完善与拓展已成为亟待研究解决的重要问题。
直觉模糊集(Intuitionistic fuzzy sets,IFS)作为模糊理论的重要扩充和发展,其数学描述更加符合客观世界的模糊本质,为不确定信息的研究和处理提供了新的思路[ 7]。Castillo[ 8]首次将直觉模糊推理融入时间序列分析,提出了直觉模糊时间序列(Intuitionistic fuzzy time series,IFTS)的概念,极大地扩展了时间序列对不精确、不完备等模糊信息的处理功效。然而,关于IFTS的研究才刚刚起步,目前正处于初期理论探索阶段,缺乏标准化的体系结构,系统的泛化性能差,预测算法的适用范围有限。文献[ 9]在研究直觉模糊逻辑关系的基础上,规范了IFTS的概念,提出了基于确定性转换的IFTS预测算法,获得了较好的预测精度,但算法仅适用于短期时间范围预测,模型的实际应用范围有限。
鉴于此,本文引入易识别的滑动窗口机制获取序列数据的分布特性,在基于直觉模糊C均值(Intuitionistic fuzzy C-means,IFCM)聚类算法优化论域区间划分标准以及建立确定性转换直觉模糊规则库的基础上,提出了基于矢量量化的长期IFTS预测方法。实例验证结果表明,本文算法取得了较好的预测结果。
定义1(直觉模糊时间序列) 设{Y(t)}(t∈[1,n])为论域U上的时间序列,给定次序分割集合{Pi},其语言变量为{Li},其中i∈[1,r], 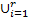
F(t)=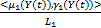 + + 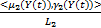 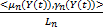 | (1) |
式中:<μi(Y(t)),γi(Y(t))>/Li表示Y(t)相对于语言变量Li及其隶属度、非隶属度函数的对应关系;“+”为连接符号。令fi(t)=<μi(Y(t)),γi(Y(t))>/Li,若将fi(t)理解为语言变量值,则F(t)作为直觉模糊集的集合就可以表示为时间t的函数。因此,IFTS的样本数据集为直觉模糊集。
定义2(直觉模糊时序关系) 设F(t)为给定论域U上的IFTS,则其时序关系式可表示为:
F(t)=(F(t-1)*F(t-2)*…*F(t-m))°Rw(t,t-m) (2)
式中:Rw(t,t-m)=<μR(t,t-m),γR(t,t-m)>为直觉模糊关系矩阵;w为滑动窗口宽度;如果F(t)仅由F(t-1)确定,或者仅由F(t-2)确定,或者仅由…确定,或者仅由F(t-m)(m>0)确定,则“*”取直觉模糊并运算;否则,若F(t)由F(t-1),F(t-2),…,F(t-m)同时确定,则“*”取直觉模糊交运算;本文取合成运算符“°”为“∧-∨”运算。
定义3(直觉模糊范数) 设A=<μA(xi),γA(xi)>,B=<μB(xi),γB(xi)>为论域∨上的直觉模糊集,依据欧氏距离定义直觉模糊范数为
‖A-B‖=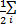 [(μA(xi)-μB(xi))2+(γA(xi)-γB(xi))2+…+(πA(xi)-πB(xi))2 [(μA(xi)-μB(xi))2+(γA(xi)-γB(xi))2+…+(πA(xi)-πB(xi))2 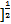 | (3) |
式中:πA(xi),πB(xi)分别表示A、B的犹豫度参数。
定义4(矢量量化) 设给定包含w维向量的数据集 D r。矢量量化方法是指尝试确定预定义的最佳量化数值 M j( j∈[1, c]),通过计算数据向量坐标的最近质心,估计预测值可定位于其质心的相应坐标,以此降低测量数据间的误差。而且一旦编码器生成,根据码本学习理论,每个 D r就被距离最近的质心 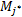
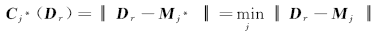
式中:“ 
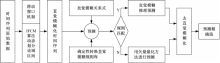
关于模糊时间序列预测的研究大多都采用短期趋势预测方法,即一个预测步骤只能预测一个未知值,而长期时间序列预测是指一个预测步骤可以获取多个待预测值,形成一个预测矢量。若利用矢量量化方法进行长期时间序列预测必将大幅提升系统的预测性能。因此,如图1所示,本文建立的长期 IFTS预测模型就是通过挖掘历史数据的模糊变化特性,基于直觉模糊逻辑规则构建确定性转换直觉模糊规则库,引入矢量量化方法对预测数据进行处理,从而减小长期时间范围预测的误差积累,提高系统的预测精度。以下对几个关键理论分别进行描述,并总结预测算法。
本文利用IFCM聚类算法优化论域区间划分标准,并在论域划分之前引入易识别的滑动窗口机制,实现序列数据的直觉模糊化预处理。
设给定长度为l的时间序列历史数据X=(x1,x2,…,xτ,…,xl),定义滑动窗口宽度w,序列前件长度p以及预测向量维数d,其中w=p+d。则序列数据的直觉模糊化预处理算法可描述为:
Step1 在时刻τ沿着X序列执行滑动窗口机制,构建X的一个子序列Sτ,可定义为: 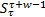
S=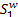 , , 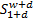 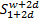 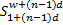 | (5) |
式中:n=(l-p)/d。
Step2 利用IFCM聚类算法对S进行聚类[ 11],获取c个聚类中心,即M={M1,M2,…,Mc}。因此,序列论域便可动态划分为c个优化子区间,其相应的语言变量直觉模糊集Aj可定义为:
Aj=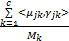 | (6) |
式中:<μjk,γjk>表示Mk属于直觉模糊集Aj的隶属度与非隶属度函数对,可按下式计算:
<μjk,γjk>=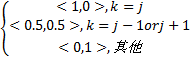 | (7) |
Step3 直觉模糊化原始序列。根据式(8)计算数据集S中所有子序列Sτ属于Aj的隶属度及非隶属度函数:
<μjτ,γjτ>=< 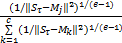
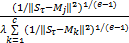
式中:e为平滑参数,通常取e=2;λ≤1为犹豫度调节因子。
因此,序列数据集X对应的IFTS可相应地表示为:F(n)=F1,F2,…,Fn,其中Fi∈{A1,A2,…,Ac}。
Step4 参考文献[ 9]动态构建确定性转换直觉模糊规则库(DCRIF_base)。
设直觉模糊化预处理后某个时间段待预测的直觉模糊时间序列为Fr=(f1,f2,…,ft,…,fr),相应的查询时间序列为X'=(x1,x2,…,xw)。可见,根据式(2),序列数据ft经推理可获得对应于X'在时刻w+(t-1)d,w+(t-1)d-(d-1),w+(t-1)d-(d-2),…的d维预测值,则其结果时间序列可表示为:
X'=(x1,x2,…,xw, 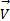
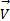
式中: 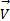
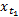
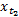
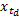
因此,基于矢量量化的长期IFTS预测算法可描述为:
Step1 确定直觉模糊观察子序列Temp F。
若r>q,需观察长度为q的直觉模糊子序列Temp F=Fr-q+s,…,Fr-1,Fr;否则,Temp F=Fs-1,Fs,…,Fr,其中s∈[1,r]。
Step2 根据观察子序列Temp F进行直觉模糊规则库的查看及匹配。
本文采用文献[ 12]中的启发式规则,如果Temp F与确定性转换直觉模糊规则i*的前件rb_cause(i*)匹配,即Temp F→rb_cause(i*),则Fr+1对应规则i*的后件,Temp Fr+1→rb_effect(i*),跳至Step4;否则,转到Step3。
Step3 矢量量化方法估计预测结果。
令Fr=Aj,Aj∈{A1,…,Ac},则IFTS中p维历史数据可表示为:past(Aj,p)=( 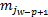
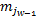
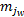
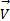
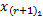
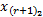
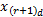
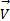
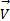
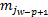
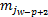
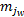
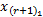
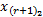
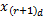
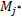
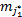
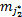
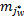
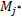
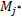
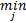
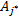
Step4 去直觉模糊化精确输出。
若IFTS预测结果为Fr+1→ 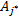
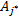
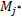
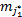
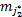
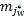
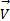
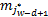
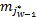

为了验证预测算法的有效性,本文采用模糊时间序列预测模型研究系列文献中的常用观测数据进行测试[ 13],其输入序列可表示为X(t)=(26.1,27.8,…,30.2),取前20天平均气温数据序列为训练样本,利用基于矢量量化的长期IFTS模型进行预测。
(1)序列数据直觉模糊化预处理
Step1 执行滑动窗口操作获取数据集S,并利用IFCM聚类算法优化区间划分。令p=2,d=2,则w=4。根据式(5)可知:S= 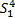
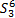
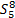

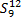
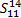



| 表1 子序列数据集取值表 Table 1 Subsequence data set values table |
Step2 构建直觉模糊时间序列及其对应的确定性转换动态直觉模糊规则库。
设定语言变量直觉模糊集:A1代表{低}、A2代表{适中}、A3代表{高},其中 A j = 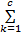
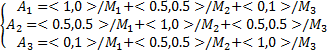 | (10) |
令犹豫度调节因子λ =0 .97。根据式(3)(8)计算数据集 S中所有子序列属于 A j的隶属度与非隶属度函数对,其结果如表2所示。
根据文献[8]关于直觉模糊期望值计算理论,观察 F( t)对 A j的期望排序,获取 IFTS为: F9 =( A1, A2, A2, A2, A3, A3, A3, A2, A2)。因此,由确定性转换直觉模糊规则库算法可知其对应规则如表3所示[ 9]。
| 表2 直觉模糊集隶属度与非隶属度函数取值表 Table 2 Numerical values for IFS membership grade and non membership grade function |
| 表3 确定性转换直觉模糊规则关系式 Table 3 Rules repository of intuitionistic fuzzy deterministic transition |
(2)基于矢量量化方法的长期IFTS预测
Step1 确定观察子序列Temp F。给定测试数据集t=1时刻的数据资料,时间序列(x1,x2,x3,x4)的直觉模糊集可表示为F1→F(1)→A3。查询序列A3的长度r=1,规则库中前件的最大长度q=3,即r
Step2 直觉模糊规则库查看与匹配。遍历查询表3描述的DCRIF_base可知,没有相匹配的规则。因此,调用矢量量化方法进行IFTS长期趋势预测。
Step3 矢量量化方法获取预测结果。首先,考察p=2维的IFTS历史数据。例如past(A3,2)=(28.15,27.32),增加预测向量进行扩展,则D2=(past(A2,2)| 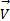
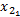
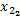
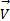
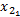
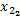
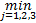
Step4 去直觉模糊化输出。由F2→A3可知,Defuzz(A3)=(29.04,28.61,28.15,27.32),则二维待预测向量可表示为: 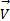
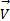
| 表4 基于矢量量化长期IFTS预测结果 Table 4 Forecasting results for Long-term IFTS based on vector quantization |
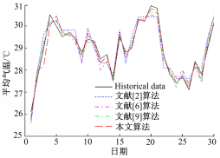
如图2所示,将本文提出的长期IFTS预测算法与几种常用的FTS预测算法进行比较,并利用度量标准中的均方差(MSE)、平均预测误差率(AFER)和算法的时间复杂度(T(n))对系统的预测性能进行测试,结果如表5所示。
| 表5 预测算法性能比较 Table 5 Performance comparison for different forecasting methods |
由此可见,短期FTS预测模型对于具有明显非线性特征的序列数据在长期趋势预测上易陷入局部收敛;基于确定性转换IFTS预测虽能从本质上把握非线性数据的波动特征,较好地反映序列数据的模糊变化趋势,但针对没有规则相匹配的长期时间范围预测,忽略了数据间的模糊依赖性,预测精度不高;基于矢量量化的长期IFTS预测算法将长期趋势预测转换为矢量预测,不仅简化了算法的复杂度,准确描述了序列数据的不确定性本质,充分考虑了历史知识对预测向量的影响,虽短期范围预测的准确度有所波动,但随着时间的延伸,系统的预测精度得到了较大的提高。
针对FTS长期趋势预测理论研究的不足,提出了基于矢量量化的长期TFTS预测方法。将序列数据由单输出扩展为多输出,预测值由标量转换为向量,较大程度地提高了TFTS的长期时间范围预测精度。文中引入滑动窗口机制,准确、快速地获取序列数据的模糊变化特征。利用IFCM聚类算法动态划分论域区间,更加接近不确定数据分布的实际。基于矢量量化的长期时间范围预测,较好地解决了直觉模糊规则零匹配以及长期趋势预测误差积累的问题。最后通过实例验证了本文模型具备较好的预测性能。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|