引用本文
田海江, 雷鹏, 王永. 基于混沌和DNA动态编码的图像加密算法. 2014, 44(3): 801-806
TIAN Hai-jiang, LEI Peng, WANG Yong. Image encryption algorithm based on chaos and dynamic DNA coding. 吉林大学学报(工学版), 2014, 44(3): 801-806  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于混沌和DNA动态编码的图像加密算法
田海江1, 雷鹏2, 王永2
1.重庆邮电大学 期刊社,重庆 400065
2.重庆邮电大学 计算机科学与技术学院,重庆400065
王永(1977),男,教授.研究方向:信息安全,混沌密码.E-mail:wangyong1@cqupt.edu.cn

田海江(1981),男,编辑.研究方向:信息安全,混沌密码.E-mail:15165789@qq.com

基金:国家自然科学基金项目(61003256, 61003246); 中国博士后基金项目(20110490082); 重庆市教委科技项目(KJ120506);
摘要

以时空混沌模型作为核心控制方程,设计了一种基于动态DNA编码的图像加密算法。该算法使用耦合映像格子(Coupled map lattices,CML)中格子的状态值来编制索引,然后根据索引值选择像素点的DNA编码规则。由于对像素点的DNA编码是动态变化的,很好地解决了DNA编码规则少所带来的安全隐患,提高了算法的安全性。在加密图像的过程中,还通过密文反馈和混沌系统的迭代来增强算法的混淆和扩散特性。仿真实验表明,算法具有很好的安全性,适合应用于图像加密。

关键词: 计算机应用; 混沌; 图像加密; DNA编码; 耦合映像格子
中图分类号:TP301 文献标志码:A 文章编号:1671-5497(2014)03-0801-06
Image encryption algorithm based on chaos and dynamic DNA coding
TIAN Hai-jiang1, LEI Peng2, WANG Yong2
1. Periodical Office, Chongqing University of Posts and Telecommunications,Chongqing 400065,China
2. College of Computer Science and Technology, Chongqing University of Posts and Telecommunications,Chongqing 400065, China
Fund:
Abstract

An image encryption algorithm based on dynamic DNA coding is proposed, which uses the spatiotemporal chaotic model as the core control function. In this algorithm, the indexes are created according to the status values of the coupled map lattices. Then, the DNA coding rules are determined by the indexes. Since the pixels are coded as different DNA bases with variable rules, the security of the encryption algorithm is improved. Moreover, the Cipher-block chaining mode and chaos iteration are employed in the encryption process to enhance the confusion and diffusion of the algorithm. Simulation experiments show that the proposed algorithm has good security and high potential to be applied in image encryption.

Keyword: computer application; chaos; image encryption; DNA coding; coupled map lattices
0 引言

图像作为多媒体中最常用的一种形式,具有数据量大、冗余度高等特点。现有的经典加密方法并不十分适用于图像加密。因此,针对图像冗余度高的特点,采用多种新技术设计图像加密算法成为了当前学术界研究的热点。

混沌系统天然所具有的初值敏感性、伪随机特性等属性非常适合用于设计加密算法[ 1]。当前,已提出了不少基于混沌的图像加密算法[ 2, 3, 4, 5]。为消除图像冗余度,文献[ 2]中提出了3种基于混沌图像置乱方法。Mao等给出了加密图像的置乱-扩散结构[ 3]。Wang等通过引入变控制参数等方式提升了安全性和效率[ 4, 5]。此外,还有一些图像加密算法使用了高维的更为复杂的混沌映射,以保证混沌序列的复杂性,进而提高算法的安全性[ 6, 7]。

1994年Adleman首次提出DNA计算[ 8]。在DNA计算中,使用碱基A,T,C和G来表示信息。文献[9]中使用2比特来表示一个碱基,即用00,01,10,11分别表示A,T,C,G。文献[10]中给出了基于DNA的代数操作,比如DNA的加法、减法以及异或等运算。Gehani等在2000年使用DNA作为信息的载体提出了一种图像加密的方法[ 11]。近年来,一些研究者将DNA的编码规则和混沌映射结合提出了一些图像加密方法[ 12, 13]。这些方法具有不错的加密效果,同时,在算法中仅使用了DNA的编码规则,不需要进行生物实验,更具实用性。因此,这类结合DNA运算与混沌特性的图像加密算法受到了众多来自不同领域的研究者的关注。

在当前提出的结合DNA编码与混沌特性的图像加密算法中,选用的DNA编码规则是固定不变的。由于DNA编码规则仅有8种,使得算法抗穷举攻击的能力很弱,容易造成安全隐患。为此,本文提出了动态的DNA编码方法,即不同像素点采用不同的DNA编码规则,同时,以时空混沌系统作为加密图像的混沌映射,将系统的状态值作为选择DNA编码的依据,从而有效地将时空混沌特性与DNA动态编码结合在了一起。本文提出的算法很好地解决了DNA编码规则少、容易被暴力攻击的弱点。同时,以时空混沌系统作为算法的控制方程,也有效避免了简单混沌系统中存在的混沌序列容易被预测的不足。因此,该算法具有很好的安全性,极具保障图像安全的应用潜力。

1 算法描述
1.1 耦合映像格子模型

耦合映像格子(Coupled map lattices,CML)是时空混沌系统中一种较为成熟的模型,本文采用它作为加密算法中使用的混沌方程,其表达式为:

=(1-ε)f( )+εf( ) (1)

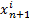
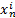
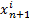
式(1)中: 为模型中第i个格子在时空n的状态值。n=1,2,…为时间索引或状态索引;i=1,2,…,N为格子的位置索引;f为局部混沌映射ε∈(0,1)表示耦合强度。

模型的边界周期条件为:xn(N+i)=xn(i)。此处,采用帐篷映射作为耦合映像格子模型的局部映射,第m个格子的局部映射如式(2)所示:

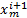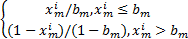= (2)

式中:b∈(0,1)为帐篷映射的控制参数。

与简单的混沌映射相比,CML模型有更为复杂的动态特性,且在有限精度下的序列周期更长,因此基于它设计加密算法,比使用简单混沌映射具有更好的安全性。随机设置CML中格子的初始值,设置N=100,ε=0.05,b=0.4999,得到模型的状态值变化情况如图1所示。从图1中可以看出,CML模型具有非常复杂的动态特性。

图1 CML模型的状态值Fig.1 Status values of CML

1.2 加密算法

本文算法中使用的DNA编码方案有8种,如表1所示。以编码方案1为例,其对应加法运算规则,如表2所示。

表1 DNA编码与解码的8种方案 Table 1 Eight schemes of DNA coding and decoding
表2 DNA编码方案为1时的加法规则 Table 2 Addition rules with DNA coding scheme 1

设需要加密的灰度图像尺寸为( m, n),采用包含8个格子的CML模型作为加密图像的混沌模型,并设置 ε=0.05。加密算法步骤描述如下。

步骤1 将图像中的像素点,按照从左到右,从上到下的顺序转换为一个序列P,以8个像素点为单位,对序列P进行分组,即:P= 为图像中对应像素点的灰度值。

步骤2 将128比特的密钥k划分为16个字节的数值,分别表示为k1,k2,k3,…,k16,使用密钥初始化时空混沌的模型的状态值和参数如式(3)(4)所示:

=ki/256 i=1,2,…,8 (3)

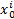
b=ki+8/256 i=1,2,…,8 (4)

步骤3 将CML模型迭代50次,消除初始值的影响。

步骤4 以CML模型中各格子的当前状态值为建立索引的依据,按照状态值从大到小的顺序为每个格子建立一个索引。即状态值最大的格子其索引为1,状态值次大的格子其索引为2,以此类推,直到所有的格子都被赋予一个索引值。令格子i对应的索引值为Indi。

步骤5 由CML中格子的当前状态值获取对应的整数值,具体规则如下:

(5)

式中:xi表示CML模型中第i个格子的状态值;函数 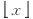表示返回不大于x的最大整数值。将Yi划分为4个2比特单元,从表1中选择第Indi个方案对其进行DNA编码,即将Yi转换了4个DNA编码。令 DNAr(Yi)表示Yi的第r个DNA编码,r=1,2,3,4。

步骤6 对于当前被处理的分组设为ωj,由分组规则知,它由8个像素点值所构成,即ωj=p8×(j-1)+1,p8×(j-1)+2,…,p8×(j-1)+8。将ωj中的每个像素点值划分为4个2比特的单元,将这些2比特单元转换为对应的DNA编码。转换规则为:对ωj中的第l个像素点p2×j+l,获取CML中第l个格子的索引值Indl,从表1中选择第Indl个方案对该像素点进行DNA编码。为描述方便,令ωj,l为分组ωj中的第l个像素点,即ωj,l=p8×(j-1)+l。与步骤4类似,ωj,l的DNA编码可以表示为 DNAr(ωj,l),r=1,2,3,4。

步骤7 根据公式(6)对当前分组ωj中像素点的DNA编码进行加密运算。

Cr(ωj,l)=( DNAr(ωj,l)+ DNAr(Yl)) DNAr(Yl)+Cr-1(ωj,l) l=1,2,…,8;r=1,2,3,4 (6)

式中:Cr(ωj,l)表示加密后的DNA编码值;Cr-1(ωj,l)表示前一个加密的DNA编码值。若 r=1,表示前一个像素点中最后一个DNA码的加密值,且C0(ω1,1)=0。

步骤8 将加密后的DNA编码根据其所属像素点的转换规则,重新解码为对应的2比特值,进而形成该像素点的密文值。

步骤9 设C4(ωj,8)解码后的2比特值为s,使用该值对CML模型的第一个格子状态值 x1进行扰动,扰动方程如式(7)所示。然后,将CML模型迭代32次。若此时图像中还有未被加密的像素点,则转步骤4,否则输出加密后的图像,加密过程结束。

x1=(x1+s/3)/2 (7)

本文算法也适用于彩色图像的加密。加密时只需将像素点的值分解为R,G和B三个单色处理即可。

1.3 解密算法

在解密过程中,CML的初始化步骤与加密算法相同,即除了在步骤1中将明文分组更改为密文分组之外,解密步骤1至5与加密过程完全相同。然后,按照与加密算法相反的顺序,执行步骤6至8中的操作。对应的解密公式如式(8)所示:

DNAr(ωj,l)=(Cr(ωj,l)-Cr-1(ωj,l)) DNAr(Yl)- DNAr(Yl) l=1,2,.…,8;r=1,2,3,4 (8)

2 安全性分析
2.1 仿真结果

密钥k为128比特,即16个字节。此处,设置密钥k所对应16个字节的值分别为{1,2,3,…,16},对512×512的标准彩色图像“Lena”和“Pepper”进行加密,对应的明文图像和密文图像如图2所示。结果显示本文的加密算法具有很好的加密效果。

图2 明文图像与其密文图像Fig.2 Plain-images and their cipher-images

2.2 密钥分析

本文算法中的密钥由16个字节构成,即长度为128比特。在当前计算机运算能力未得到突破性发展的前提下能够抵抗暴力破解的攻击。为测试算法对密钥的敏感性,在如下条件下进行实验。

条件1 将密钥所对应的字节值{1,2,…,15,16}更改为{1,2,…,15,17},对Lena图像进行重新加密,将2.1节中的密文图像与修改后的密文图像进行对比。两个密文图像之间对应像素点的不同率为99.4%。同时,使用修改后密钥解密第2.1节中加密的Lena图像,得到的解密结果如图3(a)所示。

图3 密钥微小改变条件下的解密结果Fig.3 Decryption results with key minor revision

条件2 将密钥所对应的字节值由{1,2,…,15,16}更改为{0,2,3,…,15,16},同样进行条件1中的实验操作,得到使用不同密钥加密的密文图像之间的差别为99.6%。解密图2所示的Lena密文图像的结果如图3(b)所示。

从上述实验中可以看出,对密钥进行微小的修改(更改1个比特)后,密文像素点之间的差别在99%以上,且根本无法恢复出明文图像。因此,本文提出的加密算法对密钥有很好的敏感性,且能够抵抗暴力攻击,具有很好的密钥安全性。

2.3 抗差分攻击分析

为测试图像加密算法抗差分攻击的能力,文献[3]中引入了两个数量指标:NPCR和UACI,其计算公式如下:

NPCR= ×100 %(9)

UACI= ×100 %(10)

式(9)(10)中:NPCR表示像素点改变率;UACI表示像素值的平均改变量;C1和C2表示两个仅有一个像素点存在差异的明文图像所对应的密文图像;C1(i,j)和C2(i,j)分别表示对应密文图像的第i行和第j列的像素点的值;W和H分别为图像的宽度和高度;D(i,j)的值由C1(i,j)和C2(i,j)确定,当C1(i,j)=C2(i,j)时,D(i,j)=0,否则D(i,j)=1。

选择若干幅标准灰度图像进行抗差分攻击的测试,得到的结果如表3所示。从表3中可以看出:对于不同的图像,算法的NPCR和UACI值均在99%和33%以上,因此算法具有很好的抗差分攻击能力。

表3 NPCR和 UACI的测试结果 Table 3 Test results of NPCR and UACI
2.4 抗统计攻击分析

本文从以下3个方面测试算法的抗统计攻击能力。

(1)直方图分析

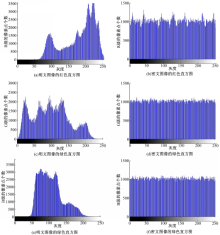
对于图2中的彩色Lena图像和它的密文图像的R,G和B 3个单色做直方图分析,得到的结果如图4所示。从图4中可以看出,密文图像的R,G和B各分量都具有均匀的分布,说明密文图像很好地隐藏了统计信息。

图4 直方图分析Fig.4 Histogram analysis

(2)相关性分析

图像的像素点之间的相关性的计算公式如下:

cov(x,y)=E{(x-E(x))(y-E(y))} (11)

rxy=(12)

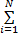
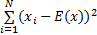
式(11)(12)中:x和y为相邻的两个像素点的灰度值,且 E( x) =( xi)/N;D(x)={ /N, N为像素点对的总数。对于彩色 Lena图像和它的密文图像,分别在水平、垂直和对角线方向上随机选取邻近的像素点1000对,并计算这些像素点对的相关性,其结果如表4所示。由表4中可以看出,邻近的明文像素点之间的相关性很大,而密文像素点之间几乎不具有相关性。这说明加密算法很好地消除了密文图像中的冗余信息。

表4 明文图像和密文图像的相邻像素点对的相关性 Table 4 Correlation of neighbor pixels pairs of plain-image and cipher-image

(3)信息熵分析

设信息为m,则其信息熵的计算式为:

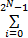
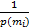
H( m) = p(mi) log bits(13)

式中:p(mi)表示信息值mi出现的概率。

假设信息m共有28种状态值且出现的概率相同,则根据式(13)得 H( m)=8,这表明信息是完全随机的。因此对密文希望其信息熵尽可能地接近于理想值8,如若信息熵小于8,则表明从理论上看密文存在一定程度的信息泄露。

对一些典型的标准灰度图像进行加密,计算密文图像的信息熵,得到的结果如表5所示。从表5中可以看出所有密文图像的信息熵均非常接近理想值8,表明密文的信息泄露极小,算法是安全的。

表5 信息熵测试结果 Table 5 Test results of information entropy
2.5 对比分析

与文献[ 3, 4, 5, 6]的基于混沌的图像加密算法相比,本文算法具有很好的抗统计攻击能力。在抗差分攻击能力方面,文献[ 4, 5]与本文算法性能相当。但文献[ 3, 4, 5, 6]的NPCR和UACI值分别为50.23%,25.23%和41.962%,33.25%,其抗攻击能力远低于本文算法。

文献[ 11, 12]与本文类似,均是基于混沌和DNA编码的图像加密算法,它们的抗统计攻击和抗差分攻击的能力与本文相当。但是,这两个算法在进行DNA编码时,使用的规则是固定不变的,而本文算法是动态变化的。此外,文献[ 11, 12]中使用的混沌方程的复杂程度也逊于本文使用的CML模型,因此,本文算法具有更高的整体安全性。

3 结束语

本文将时空混沌模型和DNA编码结合,提出了一种新的图像加密算法。利用CML格子的状态值作为挑选DNA编码规则的依据,从而使得像素点的DNA编码是动态变化的,有效提高了算法的安全性。另外,使用了密文反馈的方式对CML格子的状态值进行了微调,并利用混沌模型的迭代将密文反馈的影响进行扩大,从而使得算法具有很好的混淆与扩散特性。仿真实验的结果表明:本文提出的算法具有很好的安全性和应用潜力。

The authors have declared that no competing interests exist.

参考文献
[1] 黄润生. 混沌及其应用[M]. 武汉: 武汉大学出版社, 2000. [本文引用:1]
[2] Fridrich J. Symmetric cipher based on two dimensional chaotic maps[J]. International Journal of Bifurcation and Chaos, 1998, 8(6): 1259-1284. [本文引用:2] [JCR: 0.921]
[3] Chen G, Mao Y, Chui C K. A symmetric image encryption scheme based on 3D chaotic cat maps[J]. Chaos, Solitons & Fractals, 2004, 21(3): 749-761. [本文引用:4] [JCR: 1.246]
[4] Wang Yong, Wong Kwok-Wo, Liao Xiao-feng. A chaos-based image encryption algorithm with variable control parameters[J]. Chaos, Solitons & Fractals, 2009, 41(4): 1773-1783. [本文引用:5] [JCR: 1.246]
[5] Wang Yong, Wong Kwok-Wo, Liao Xiao-feng, et al. A new chaos-based fast image encryption algorithm[J]. Applied Soft Computing, 2011, 11(1): 514-522. [本文引用:5] [JCR: 2.14]
[6] Behnia S, Akshshani A, Mahmodi H, et al. A novel algorithm for image encryption based on mixture of chaotic maps[J]. Chaos, Solitons & Fractals, 2008(35): 408-419. [本文引用:3] [JCR: 1.246]
[7] Zhu He-gui, Zhao Cheng, Zhang Xiang-de. A novel image encryption-compression scheme using hyper-chaos and Chinese remainder theorem[J]. Signal Processing: Image Communication, 2013, 6(28): 670-680. [本文引用:1] [JCR: 1.286]
[8] Adleman L M. Molecular computation of solutions of combinational problems[J]. Science, 1994, 266(11): 1021-1024. [本文引用:1]
[9] Wasiewicz P, Mulawka J J, Rudnicki W R, et al. Adding numbers with DNA[J]. IEEE International Conference on Systems Man and Cybernetics, 2000, 21(1): 265-270. [本文引用:1]
[10] King O D, Gaborit P. Binary templates for comma-free DNA codes[J]. Discrete Applied Mathematics, 2007, 155(5): 831-839. [本文引用:1] [JCR: 0.718]
[11] Gehani A, Labean T, Reif J H. DNA-based cryptography[J]. Aspects of Molecular Computing, 2004, 54(3): 167-188. [本文引用:3]
[12] Wei Xiao-peng, Guo Ling, Zhang Qiang, et al. A novel color image encryption algorithm based on DNA sequence operation and hyper-chaotic system[J]. The Journal of Systems and Software, 2012, 85(2): 290-299. [本文引用:3]
[13] Zhang Qiang, Guo Ling, Wei Xiao-peng. Image encryption using DNA addition combining with chaotic maps[J]. Mathematical and Computer Modelling, 2010, 52(11-12): 2028-2035. [本文引用:1] [JCR: 1.42]