刘强(1985),男,博士研究生.研究方向:高精度时间同步技术.E-mail:dreamlq@163.com
建立了基于自回归算法的钟差预报模型,利用具有较强非线性运算能力和容错能力的最小二乘-支持向量机算法来求解自回归参数,同时利用具有快速寻优特点的粒子群算法来优化最小二乘-支持向量机参数。为了克服粒子群算法容易陷入局部极值而形成早熟的缺点,提出了分别在粒子初始化位置和陷入局部极值的位置上进行混沌处理,提高了粒子搜索的遍历性和寻优能力,从整体上优化了算法。最后通过星载钟差数据对该算法进行了验证,结果表明:本文算法能够实现亚纳秒量级的预报精度并提升卫星授时导航性能。
A model of Auto Regressive (AR) algorithm is established to predict clock error. The model takes the advantage of strong abilities of non-linear operation and fault toleration of Least Square-Support Vector Machine (LS-SVM) to determine the parameters of AR. It also optimizes the LS-SVM parameters by Particle Swarm Optimization (PSO), which could search the best target fast. In order to overcome the shortcoming that PSO always plunges into local extremum and becomes premature, Chaos theory is introduced into positional initialization and local extremum condition, which improves particles' ergodicity and the ability of optimization, accordingly the algorithm as a whole is optimized. The algorithm is tested by satellite clock error data. The results show that the algorithm can achieve sub-nanosecond prediction precision, thus improving the satellites' time service and navigation.
由于卫星和地球的相对位置和卫星运行空间环境的影响,在特定的时段中,卫星钟源无法与地面钟源进行实时时间对比,因而需要根据已有的钟差数据对钟差进行预报,以维持星载钟源的高精度运行[ 1]。常用的钟差预报模型有多项式模型、谱分析模型、自回归模型、灰色模型、Kalman滤波模型等。其中谱分析模型和灰色模型适合于长期预报,而多项式模型、自回归模型和Kalman滤波模型等适合于短期预报[ 1, 2]。
文献[ 1]针对线性组合模型,提出了学习权的概念,修正了组合预报模型,在保证稳定性的基础上提高了预报结果的准确性和稳定性。文献[ 3]将抗差等价权引入钟差预报,按不同采样率和时间跨度进行计算分析,得出改进的AR模型能够实现预报6 h钟差RMS在1 ns左右的结论。文献[ 4]提出了用滑动窗技术划分数据,利用神经网络预报小波分解和去噪后的钟差序列各层系数,较好地逼近了钟差序列。文献[ 5]建立了基于鲁棒LS-SVM算法的ARMA时序预报模型,算例表明该算法具有较高的预报精度和稳定性。文献[ 6]将LS-SVM算法与ARMA算法结合,通过在化工领域的应用表明该软测量模型具有较好的泛化能力和预报精度。文献[ 7]利用粒子算法(PSO)来寻优SVM参数,避免了人工搜索的盲目性,提高了模型的训练速度和预报能力,但存在PSO算法易早熟的缺点。文献[ 8]将混沌理论引入粒子群寻优算法中,克服了标准粒子群容易陷入局部极值点的缺陷,通过实例证明了该算法的有效性。
本文采用自回归模型进行钟差预报分析,利用LS-SVM算法对AR钟差预报模型进行学习训练。同时将PSO算法与SVM算法相结合进行参数选择,并将混沌理论引入其中,从而克服PSO算法易早熟的缺陷,并通过算例分析验证了本文算法能够实现亚秒量级的预报精度。
自回归AR( p)模型主要用于研究时间序列,描述某些变量自身在不同时刻的相关性,在故障预报、自然灾害预报、经济预报和系统辨识等领域有着广泛的应用,其表达式为:
xn= 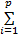
式中:en为均值为零、方差为 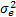
确定p比较困难,取较小的阶次则拟合程度较差;取较大的阶次时则受偶然的因素影响较大,因而确定的最佳准则函数需是一个依赖于样本数和阶次的函数,使其最小。国内外学者普遍采用的准则有AIC准则、BIC准则、FPE准则等,其中AIC(Akaike's information criterion)准则又称为最小信息准则,是由Akaike于1973年提出的,其基本思想是根据模型预报误差判断回归阶数p是否合适,从而对时间序列进行预报[ 5]:
AIC(p)= ln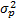 + + 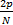 | (2) |
式中:N为样本数; 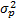
等式右边第1项体现了模型拟合程度的好坏,随着阶次的增加而减小,第2项为增加阶次后的惩罚。
为了确定模型系数,常采用最小二乘支持向量机算法,如式(3)(4)所示:
minJ= en2+ en2+  | (3) |
s.t. xn= 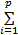
式中:γ为惩罚项系数。
根据最小化目标函数,定义Lagrange函数为:
L=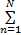 βn[ βn[ 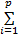 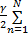  | (5) |
式中:βn∈R。
根据KKT(Karush-Kuhn-Tucker)定理,对L求偏导数得:
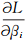
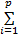
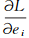
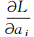
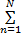
结合SVM推理过程,整理式(6)~(8)可得:
xn= 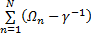
核函数Ωn有多种选择,包括线性核函数、多层感知核函数、多项式核函数和高斯径向基核函数等,本文采用高斯径向基核函数:
Ωn= exp( 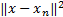
式中:δ为核宽度。
参数γ和δ的选择是算法估计性能的关键,γ用来权衡样本误差及结构风险;δ与学习样本的输入宽度有关。本文采用粒子群算法来实现参数优化。
PSO算法是美国学者Kennedy和Eberhart受鸟群觅食行为启发而提出的一种群体智能算法[ 9]。标准PSO算法在运算初期收敛速度较快,随着寻优计算的深入,粒子速度明显减小,且粒子表现强烈的趋同现象,容易陷入局部极值而形成早熟,标准PSO算法简述如下[ 10, 11, 12]:
设搜索空间为d维,粒子数为l,第i个粒子位置设为Yid=(yi1,yi2,…,yid);其最优历史位置Pid=(pi1,pi2,…,pid);Pgd为整个种群中过去最优位置;飞行速度为Vid=(vi1,vi2,…,vid)。各粒子位置和速度的更新迭代如式(11)~(13)所示:
vid(t+1)= 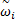
yid(t+1)=yid(t)+vid(t+1) (12)
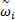
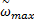
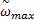
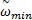
式中:c1、c2为学习因子,一般取c1=c2=2;r1和r2为介于[0,1]之间的随机数; 
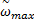
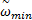
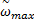
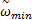
为了克服标准PSO算法易早熟的缺陷,提高粒子的全局寻优能力,许多学者提出将混沌理论引入PSO算法中,取得了较为满意的效果。胥小波等提出将混沌融入粒子运动过程,使粒子在混沌与稳定之间交替运动,从而实现全局寻优,通过数值测试结果证明该方法能极大提高计算精度和寻优能力[ 13]。文献[ 14]在标准PSO算法寻求的最优位置上加入混沌扰动,使得粒子跳出局部极小,取得了较好的效果。本文将混沌加扰动思想分别加入到粒子初始位置和最优位置上,充分利用混沌理论的遍历性来克服局部极小,实现全局最优。在初始位置加入混沌序列,能够充分利用PSO算法前期的快速寻优和算法简单的特性,同时能够利用混沌的遍历性提高粒子的寻优能力;在局部最优的位置上引入混沌思想则可使PSO跳出局部极值点而实现全局最优。本文采用Logistic方程来产生混沌序列,如式(14)所示:
zk+1=μzk(1-zk),k=0,1,2,… (14)
当z0∈(0,1)、z0∉{0.25,0.5,0.75}且μ=4时,已经证明该序列是完全混沌的。
采用CPSO优化LS-SVM的γ和δ的算法进行钟差预报的具体步骤如下所示。
步骤1 初始化算法参数包括:粒子初始位置、速度、最大迭代次数G max、种群规模和最大最小惯性权值、学习因子、训练样本数m等,同时定义粒子的适应度函数为:
Fi=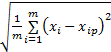 | (15) |
式中:xi为实际钟差值;xip为预报钟差值。
设种群规模d=2,随机产生一个取值在(0,1)间的二维向量 y1 =( y11, y12),根据式(14)依次产生 N个向量即为初始种群位置。
步骤2 计算并比较各粒子的适应度值 F i,如果粒子当前适应度值 F i <F ibest(该粒子所经历的历史最优适应度值),则将当前 F i设为 F ibest,同理若当前粒子最优适应度值 F ibest <F gbest(当前粒子种群的最优适应度值),则将 F ibest设为 F gbest。
步骤3 判断是否早熟。若是,则引入混沌变量;若否,则转入步骤4。当粒子早熟时,设当前最优位置为 y ki,则将 y ki作为混沌算法中的初始位置 z ki,按照式(14)计算 z( k+1) i,以此替代此前陷入局部极小的粒子位置后转入步骤4。
为了避免人为判断粒子早熟的主观影响,本文引入定量计算来判断粒子是否早熟,如式(16)所示[ 15]:
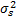 = = 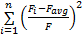 | (16) |
式中: 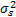
F=max 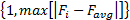
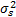
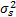
步骤4 依据式(11) ~(13)更新粒子的位置、速度和惯性权值,判断是否达到 Gmax。若是,则退出迭代,所得最优位置即为 γ和 δ取值;若否,则继续迭代直至迭代结束。
为了验证上述算法,本文根据 IGS官方网站公布的 GPS卫星钟差数据,采用2012年7月22日( MJD56130)的数据计算分析,根据卫星及星载钟源的不同类型,随机选取 PG12和 PG20星载钟源钟差数据进行验证分析。
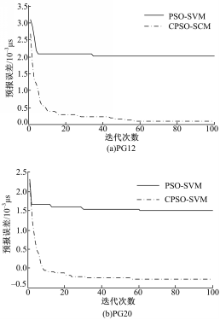
根据短期钟差预报原则和 IGS数据格式( IGS数据以天为单位记录,每15 min记录一次各卫星参数值(称为一个时段),全天共96个数据值),采用 PG12和 PG20星载钟源的钟差数据进行迭代运算,分别运用本文算法和不加入混沌算法的 PSO-SVM算法进行对比分析,迭代次数选为100次,采用前86个时段钟差数据预报第87个时段的钟差值,迭代运算结果如图1所示。
从两颗星载钟源的钟差预报误差与迭代次数曲线可知,随着迭代次数的增加,预报误差逐渐减小最终趋于稳定。从图1可知:本文在粒子初始位置和局部极值处引入混沌算法能够使粒子跳出局部极值,实现全局寻优,因而明显降低了钟差预报误差,两颗星载钟源的预报精度均在亚纳秒量级。
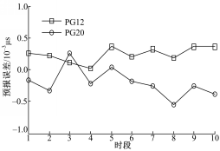
针对短期预报,在一天的钟差数据中,为了更明显地体现算法寻优性能,采用前86个时段钟差数据预报最后10个时段的钟差。结合PG12和PG20的钟差数据,分别采用本文算法进行计算,其预报结果如图2所示。
从图2中可知:两颗星载钟源的预报误差均达到了亚纳秒量级精度,同时由于星载钟源性能和所处环境、位置等差异的影响,预报误差性能存在一定程度的差异。相对目前纳秒量级的预报精度,运算结果表明本文算法能较大地改善预报精度,提高卫星钟差预报水平,从而进一步改善卫星无法与地面实时比对时的授时、导航和定位等功能。
利用自回归算法对星载钟源的钟差预报进行建模分析,综合利用最小二乘支持向量机、粒子群和混沌算法等理论对模型进行优化和改善,结合两颗星载钟源的钟差数据实例验证了算法有效性。运算结果表明:本文算法能够使算法摆脱局部极值,实现全局寻优和亚纳秒量级的卫星钟差预报精度,在卫星星载钟源无法与地面钟源实时比对的情况下,提升卫星的授时、导航等性能。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|